№	Пользователь	Рейтинг
1	jiangly	3898
2	tourist	3840
3	orzdevinwang	3706
4	ksun48	3691
5	jqdai0815	3682
6	ecnerwala	3525
7	gamegame	3477
8	Benq	3468
9	Ormlis	3381
10	maroonrk	3379

№	Пользователь	Вклад
1	cry	168
2	-is-this-fft-	165
3	Dominater069	161
4	atcoder_official	160
4	Um_nik	160
6	djm03178	157
7	adamant	153
8	luogu_official	151
9	awoo	149
10	TheScrasse	146

1. Mean

$$$ \text{Arithmetic Mean (AM)}: \quad AM = \bar{X} = \frac{\sum_{i=1}^{n} X_i}{n} $$$ $$$ \text{Geometric Mean (GM)}: \quad GM = \sqrt[n]{X_1 X_2 \dots X_n} = \left( \prod_{i=1}^{n} X_i \right)^{\frac{1}{n}} $$$ $$$ \text{Harmonic Mean (HM)}: \quad HM = \frac{n}{\sum_{i=1}^{n} \frac{1}{X_i}} $$$ $$$ \text{AM-GM-HM Inequality}: \quad AM \geq GM \geq HM $$$ $$$ \text{Frequency Distribution:} $$$ $$$ \begin{array}{|c|c|} \hline \text{Value } X_i & \text{Frequency } f_i \\ \hline X_1 & f_1 \\ X_2 & f_2 \\ ... & ... \\ X_n & f_n \\ \hline \end{array} $$$ $$$ \text{Mean for Grouped Data:} \quad \text{Mean} = \frac{\sum_{i=1}^{n} f_i \cdot X_i}{\sum_{i=1}^{n} f_i} $$$ $$$ \text{Cumulative Frequency:} \quad \text{Cumulative Frequency} = \sum_{i=1}^{k} f_i $$$ $$$ \text{Mean for Continuous Data:} \quad \text{Mean} = \frac{\sum_{i=1}^{n} f_i \cdot M_i}{\sum_{i=1}^{n} f_i} $$$

2. Median

$$$ \text{Median for Univariate Data:} $$$ $$$ \text{If } n \text{ is odd:} \quad \text{Median} = X_{\left(\frac{n+1}{2}\right)} $$$ $$$ \text{If } n \text{ is even:} \quad \text{Median} = \frac{X_{\left(\frac{n}{2}\right)} + X_{\left(\frac{n}{2} + 1\right)}}{2} $$$ $$$ \text{Median for Grouped Data:} \quad \text{Median} = L + \left( \frac{\frac{n}{2} - F}{f} \right) \cdot h $$$ $$$ \text{Explanation of Terms:} $$$ $$$ X \quad \text{: The values in the dataset, ordered from smallest to largest.} $$$ $$$ n \quad \text{: Total number of data points or observations.} $$$ $$$ L \quad \text{: Lower boundary of the median class in grouped data.} $$$ $$$ F \quad \text{: Cumulative frequency before the median class.} $$$ $$$ f \quad \text{: Frequency of the median class.} $$$ $$$ h \quad \text{: Class width for grouped data.} $$$

3. Mode

$$$ \text{Mode for Univariate Data:} $$$ $$$ \text{Mode} = \text{the most frequent value in the dataset (for unimodal data)} $$$ $$$ \text{Mode} = \text{list of most frequent values (for multimodal data)} $$$ $$$ \text{Mode for Grouped Data:} \quad \text{Mode} = L + \left( \frac{f_1 - f_0}{(2f_1 - f_0 - f_2)} \right) \cdot h $$$ $$$ \text{Explanation of Terms:} $$$ $$$ L \quad \text{: Lower boundary of the modal class.} $$$ $$$ f_1 \quad \text{: Frequency of the modal class.} $$$ $$$ f_0 \quad \text{: Frequency of the class before the modal class.} $$$ $$$ f_2 \quad \text{: Frequency of the class after the modal class.} $$$ $$$ h \quad \text{: Class width for grouped data.} $$$

Measure of Location

A measure which is located in different place in the array is called the measure of location. Median is one kind of measure of location, because median divided whole data set with two parts.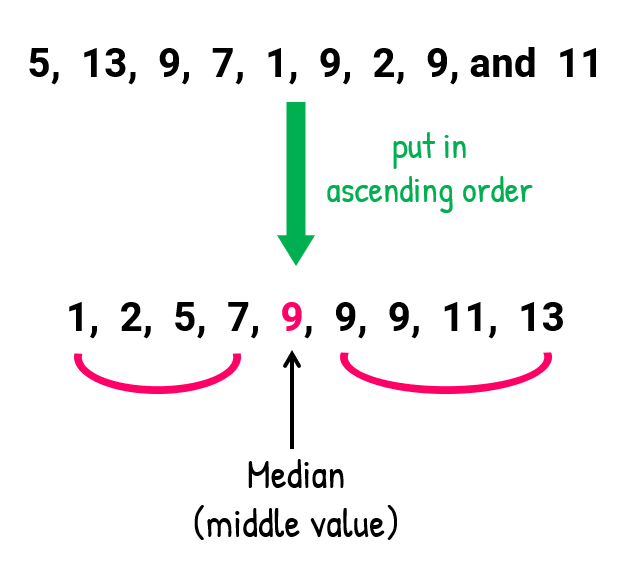

Why important measure of location?

If you need any number in a data set which is divided the whole data set with in 1:3. It means left side of this set has 1/4 of data and right side has 3/4 data. Most frequently used measure of locations are :

1. Median :

2. Quartile:

Quartiles divide the data into four equal parts. First Quartile (Q1): The median of the lower half of the data (25% of the data is below Q1). Second Quartile (Q2): The median of the data (50% of the data is below Q2). This is the same as the median. Third Quartile (Q3): The median of the upper half of the data (75% of the data is below Q3).

$$$ \text{Quartiles:} $$$ $$$ Q1 \quad \text{(First Quartile)} = \text{Median of the first half of the data.} $$$ $$$ Q2 \quad \text{(Second Quartile)} = \text{Median of the dataset.} $$$ $$$ Q3 \quad \text{(Third Quartile)} = \text{Median of the second half of the data.} $$$

3. Decile :

Deciles divide the data into ten equal parts. Each decile represents 10% of the data.

$$$ \text{Deciles:} $$$ $$$ D_n = \frac{n}{100} \cdot (N + 1) $$$ $$$ \text{where } n \text{ is the decile number (1 to 9) and } N \text{ is the total number of data points.} $$$

4. Percentile :

Percentiles divide the data into 100 equal parts. Each percentile represents 1% of the data.

$$$ \text{Percentiles:} $$$ $$$ P_n = \frac{n}{100} \cdot (N + 1) $$$ $$$ \text{where } n \text{ is the percentile number (1 to 100) and } N \text{ is the total number of data points.} $$$