Блог пользователя Gerald

Задача на префикс функцию
Автор Gerald, 14 лет назад, По-русски
Собственно задача состоит в следующем, есть строка зашифрованная по RLE, т.е. представленная в виде (x1)k1(x2)k2...(xn)kn, где (xi)ki означает строку из символов ki длины xi (например строку AAABBCCC можно представить в виде (3)A(2)B(3)C). Нужно отвечать на запросы Qi, вывести Prefix(Qi). (Prefix(i) - префикс функция i-го префикса строки). 

Ограничения: ki до 109, Количество блоков в RLE до 50000, запросов 105.

Предлагаю совместными усилиями "одержать" эту задачу. =)
  • Проголосовать: нравится
  • +13
  • Проголосовать: не нравится

14 лет назад, # |
← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится
Наверно как нибудь хэшами и бинарным поиском по значению префикс ф-ии. Правда хэш ф-я будет считаться за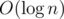 и в итоге время будет .
→ Ответить
  • 14 лет назад, # ^ |
      Проголосовать: нравится +6 Проголосовать: не нравится
    Хэшами с префикс функцией не особо получится имхо. Например строка abababab для последней позиции b будет чередоваться значение функции существование префикса равного суффиксу.
    → Ответить
14 лет назад, # |
← Rev. 2   Проголосовать: нравится +5 Проголосовать: не нравится
Есть одна идейка. Она правда еще не закончена, но может кому-то поможет эта идея, чтобы окончательно решить задачу.
Попробовать воспользоваться тем, что из Z-функции можно получить префикс функцию.

В Гасфилде, например, следующим образом это делается:
p'[i] = 0, для всех i, а затем, для каждого j: p'[j + z[j] - 1] = z[j]
тогда префикс функция p[i] = max(p[i + 1] - 1, p'[i])

Теперь сама мысль как считать z-функцию:
я думаю, что достаточно посчитать ее не для всех блоков, а только следующих:
рассмотрим k_i == k_1 (для остальных z равна нулю):
1) x_i < x_1, то где бы в блоке префикс не начался, он в этом же блоке и закончится и будет влиять только сам блок (это можно отдельно как-то учесть)
2) x_i >= x_1, тогда 
2.a) если мы будем начинать строку в начале блока i (т.е. если отсчитывать от начала блока, то < x_i - x_1), то она опять же в самом блоке и закончится (как в 1)
2.b) если начнем после позиции x_i - x_1, то опять закончится в этом же блоке
2.с) начнем ровно в позиции x_i - x_1, тогда у нее будет возможно продолжение, которое распространится на остальные блоки.
Предлагаю для всех случаев 2.с посчитать Z-функцию (их будет не более, чем n), можно хэшами или за n^2 в крайнем случае. 
Затем посчитаем p'[] разряженно (там будет не более n элементов). 
Тогда чтобы считать p[i] нужно следующее: если p'[i] для этой позиции есть, то возьмем его, и теперь нам надо сделать max(p[i + 1] - 1, p'[i]) но p[i + 1] нам не известно, но так как они все рассчитываются из p'[j], то можно p[i] заменить как на max(p'[j] - (j - i)) для всех j >= i, т.е. надо научиться считать такую функцию на суффиксе. 
Это вроде не сложно делать. Можно идти с конца по запросам (по невозрастанию q_i) и складывать p'[] в set, и поддерживать величину sub -- сколько мы вычитаем из всех элементов в set, будет что-то типа sub -= lastP' - j set.insert(p'[j] + sub); и выбирать из сета потом максимальный.

Для 2.а и 2.b надо учесть еще z-функции которые заканчиваются в самом блоке. Тут надо еще подумать какие именно. Но вроде если позиция для которой считаем префикс функцию находится относительно начала блока k_j == k_1, в позиции до x_1, то для этого достаточно еще считать z-функцию для начала таких блоков, если начинается после x_1, то можно брать p'[i] == x_1.


→ Ответить
  • 14 лет назад, # ^ |
      Проголосовать: нравится +5 Проголосовать: не нравится
    Отличная Идея =)
    По сути та формула для префикс функции, которую ты написал, просто означает, что префикс функция для позиции i некоторой соответствующей z-функции, которая начинается не позже чем i и своей длиной как бы перекрывает позицию i, минус немного (хвост который вылезает за i). 

    Чем это нам помогает, тем что можно подробить нашу RLE в случае 2c + дополнительно подробить когда мы считаем p'. Дробить будем таким образом чтобы каждый случай 2с начинался с отдельного блока и каждое значаение p' было в конце некоторого блока. Так же придется сохранить отдельно недробленую RLE. Теперь пойдем с от конца строки к началу при этом будем поддерживать указатели на текущий блок в дробленом и недробленом виде и будем считать запросы, приблизительно так как ты написал с сетом. так мы учтем все случаи 2с. Случаи 2а и 2b: во первых нужно понятно, что их надо учитывать только в том случае, если первая буква строки совпадает с буквой текущего блока (эти случаи не выходят за границу блока), во вторых мне кажется просто можно взять максимум из текущего ответа с учетом 2с и что-то типа min(CurrentPosition-BlockStart+1, FirstBlockLength). =)


    → Ответить
    • 14 лет назад, # ^ |
      ← Rev. 2   Проголосовать: нравится +5 Проголосовать: не нравится
      После того как подробим RLE, можно для блоков найти z[] за линию обычным z-алгоритмов, а потом расширить их, при необходимости (т.е. это в случае если k[z[i]] == k[i + z[i]], то z[i] += min(x[z[i]], x[k + z[i]]).
      А последний этап можно даже вроде без сета сделать, просто поддерживая максимальное из z - текущая позиция.
      И в сумме тогда линейный алгоритм получится.
      UPD. Не получится линейный :(. Запросы надо сортить...
      → Ответить
  • 14 лет назад, # ^ |
    ← Rev. 2   Проголосовать: нравится +3 Проголосовать: не нравится
    Сдал таки =)
    Кому интересно -- мой код: http://www.everfall.com/paste/id.php?jjrp36xwg3x6
    Там как оказалось могут быть строки еще такие: XaYa из-за этого код немного больше. И еще некоторые нюансы возникли, когда у блока i с таким же символом как  у первого x_i > 2 * x_1.
    В коде: 
    normalize - приводит строку к удобному виду, сначала XaYa -> (X+Y)a, а потом, для всех блоков i, где k_i == k_1 и x_i > x_1 разбивает на две части -- x_i - x_1 и x_1.

    zfuncBlocks - считает z-функцию для строки где каждый символ это блок.
    zfunc - считает z-функцию для начала каждого блока нормализированной строки. Делает это расширяя zfuncBlocks -- добавляя префиксы блоков, до которых "дотягивается" z-функция.
    Т.е.: было 1a5b1a2b  zfunc вернет для 3его блока 1 (1a == 1a), но нам надо расширить это значение, так как следующие, за блоками, символы равны, надо тогда увеличить значение z-функции на min(5, 2). 

    prefix - считает префикс-функцию для нужных позиций, сначала идет расчет z-функции, потом считается p' (ps) потом для каждого блока i считается minp[i] - минимальное среди всех j >= i значение j - p'[j] + 1 (это будут возможные начала суффиксов). А дальше обрабатывая запросы от больших к меньшим считает префикс функцию используя minp.

    Сложность O(M*log(M) + N*log(N)) получилась. Из этого можно сделать O(M*log(M) + N) но при этих ограничениях толку особо нет.
    → Ответить
14 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится
Какая максимальная величина запроса?
→ Ответить
  • 14 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится
    Если q_i будет не большим, то задача особо смысла не имеет, можно разжать нужный префикс и посчитать в лоб.
    → Ответить
    • 14 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится
      Это понятно. Я просто неправильно посчитал максимальную длину строки, думал она супер большая.
      → Ответить
14 лет назад, # |
← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится
ignore
→ Ответить
14 лет назад, # |
  Проголосовать: нравится +5 Проголосовать: не нравится
А это попробовать сдать где-нибудь можно? Или это пока просто в виде идеи?
→ Ответить
  • 14 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится
    Думаю, что особо это сдать негде. В проблемсетах я её не видел, только однажды на контесте, архивы которого не распростроняются.
    → Ответить
  • 14 лет назад, # ^ |
      Проголосовать: нравится +5 Проголосовать: не нравится
    Оно? :)
    → Ответить
    • 14 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится
      Оно, спасибо =) Попробую сдать =)
      → Ответить
    • 14 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится
      Только у меня "оно" лежит?
      → Ответить
      • 14 лет назад, # ^ |
          Проголосовать: нравится 0 Проголосовать: не нравится
        Оно не лежит, там надо залогинится, чтобы посмотреть задачу, иначе ошибку выдает.
        → Ответить
        • 14 лет назад, # ^ |
            Проголосовать: нравится 0 Проголосовать: не нравится
          ок спасибо)
          → Ответить
        • 14 лет назад, # ^ |
            Проголосовать: нравится 0 Проголосовать: не нравится
          Что-то я залогинился всё равно ошибка =(
          → Ответить
          • 14 лет назад, # ^ |
              Проголосовать: нравится 0 Проголосовать: не нравится
            Там вроде еще надо на курс подписаться нужный.. В "выборе курсов" (сверху 3-я кнопка) -> "программирование" -> "методы алгоритмизации". Причем кнопка "сохранить" работает только под IE..
            → Ответить
14 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится
Гера я кажется знаю с какого она контеста
→ Ответить
  • 14 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится
    Да ты прав Эдик, с того самого =)
    → Ответить
    • 14 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится
      Я её когда увидел на контесте подумал халявка сща сдам. Но минут через 25-30 понял что надо браться за другую
      → Ответить
14 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится
что такое Prefix(Qi) ?
→ Ответить
14 лет назад, # |
← Rev. 2   Проголосовать: нравится +10 Проголосовать: не нравится
Не уверен, что это поможет, или что это хотя бы правда, но погенерив тесты локально я увидел, что число индексов i, таких, что P(i)!=P(i+1)-1 и P(i)!=P(i+1) очень невелико. Не знаю, всегда ли это так, но для самый хучший результат для 10000 блоков у меня был когда буквы всего 2, и это было меньше 10000. Я не уверен, что это всегда верно, но если у автора есть возможность это проверить.. 
*Интуитивно вообще кажется, что таких пар не более N^(3\2).
**Надеюсь, то, как найти конец текущего промежутка индексов, в которых значение префикс-функции возрастает/стационарно, ясно.
***Зная такие промежутки, на вопросы можно отвечать бинпоиском.
→ Ответить
  • 14 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится
    Можно поподробнее про ** и ***?
    → Ответить
    • 14 лет назад, # ^ |
      ← Rev. 4   Проголосовать: нравится +5 Проголосовать: не нравится
      ***
      Если мы знаем отсортированный список промежутков, таких что на них префикс-функция стационарна или возрастает на 1 с ростом индекса, то для каждого запроса мы можем найти, в каком промежутке он находится, с помощью БП, и зная значение П-Ф на конце промежутка, получить значение в нужной нам точке.
      ** (Сорри, после того как я это написал, понял, что "очевидно" - не самое подходящее слово, до этого сам имел только отдаленное представление)
      Предположим что сейчас мы в позиции i, а префикс-функция - в позиции j.  Очевидно, в этих позициях одинаковые буквы, один из этих блоков кончается раньше другог, скажем, через к шагов. Значит близжайшие к-1 индексов строго возрастают, а потом либо начинается новый промежуток, либо кончается текущий блок одинаковых букв ( тогда тоже будем обрывать промежуток , а потом будем мержить два возрастающих промежутка на границе блоков.)

      Теперь про стационарные. Для них можно применить похожий трюк - если у нас для двух соседних позиций значение П-Ф совпадает, то и для всех следующих индексов в текущем блоке одинаковых букв тоже будет совпадать.

      Осталось последнее - считать ПФ для первой буквы из блока одинаковых. Заметим, что ПФ от такой буквы должна либо быть равна 0 либо указывать на позицию тоже в самом начале блока, чтобы предыдущая тоже отличалась. Но таких позиций вообще говоря порядка N. Из-за этого для них ПФ можно считать втупую, потому что число прыжков тоже не превысит N в сумме, а запрос значения ПФ в ранее высчитанной точке тоже можно считать БП ( хотя можно и преподсчитать для таких позиций и отвечать за 1).
      → Ответить
      • 14 лет назад, # ^ |
          Проголосовать: нравится 0 Проголосовать: не нравится
        тпр, ну да, и естественно, каждый раз, когда у нас начинается новый промежуток внутри старого блока, нам тоже прийдется считать значение П-Ф в точке заново. Опять таки, в сумме за О(кол-во промежутков * БП для нахождения значения ПФ в точке).
        → Ответить
14 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится
А нельзя ли, как нибудь, например, считать различные пары (n,a) различными символами. ТО есть рассмотреть строку из них и построить префикс функцию обычным способом на такой вот строке.
Потом сводить исходную задачу к этому прекалку уточненяя край.
→ Ответить
14 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится
Надеюсь, что правильно прочитал и понял условие.
Исхожу из того, что возможных различных символов в строке - некоторое небольшое разумное количество (пусть для этого примера - 26). Если вдруг я ошибся, и различных возможных символов много больше - прошу прощения заранее.

Пусть n - количество блоков, m - количество запросов. Будем рассматривать префикс-функцию уровня блоков.
Тогда для каждого блока ki будем хранить:
* prefix(ki)
* elems_before(ki) - суммарное количество элементов в этом и предыдущих блоках
* таблицу prev[][], где prev[x][] - это массив, хранящий в каждой записи длину последовательности для блока kx, состоящего из символов x, такого, что он начинается сразу после одного из предыдущих префиксов (т.е. на последовательности префиксов prefix(ki), prefix(prefix(ki)) и так далее) и индекс, блока kx_prev предшествующего этому блоку kx (т.е. один из индексов prefix(ki), prefix(prefix(ki)) и т.д.). Таблицу можно упорядочить, например, по возрастанию длин, а для каждой длины хранить ссылку на блок с самым большим значением префикс-функции из тех, чьи длины больше либо равны текущей. Пусть t - количество различных длин. Таким образом, за O(log(t)) можно при необходимости находить самый длинный соответсвующий критерию поиска блок.

Скользкий момент - память для таблицы. Идея у меня - можно хранить таблицу, например, для каждого sqrt(n)-го блока (относительно обратных прыжков по значениям префикс-функции), тогда понадобится для таблиц O(n*sqrt(n)) памяти, что вполне приемлемо, вроде как. Но поиск теперь станет за O(sqrt(n) + log(t)). 

Теперь, для каждого запроса qi мы можем за O(log(n)) находить блок kqi, которому принадлежит данный индекс. Пусть смещение qi относительно kqi будет j. Далее, если этот индекс соответствует последнему элементу в блоке - мы выводим prefix(kqi). Если не последний - находим prefix(kqi - 1) (предыдущего блока) и просматриваем у него таблицу в поисках записи R с длиной большей либо равно j (за O(sqrt(n) + log(t))) так, что префикс-функция максимальна. В качестве ответа выводим elems_before(R) + j.

Получается, если я нигде не ошибся, идея решения за O(m*log(n)*(sqrt(n) + log(t))).

P.S. Было интересно подумать над этой задачей. Даже если решение ошибочное, всё равно некоторая порция удовольствия уже получена. Будет интересно посмотреть на правильное (или различные варианты такового).
→ Ответить