471A - МУХ и палочки
Нам даны длины шести палочек и надо проверить, какое животное мы может из них собрать. Единственное условие, общее для обоих животных, — четыре палочки-лапы должны быть одной длины. Так как это условие общее, то в случае отсутствия хотя бы четырех палочек одинаковой длины ответ будет однозначно "Alien". Если же такие четыре палочки есть, то кого-нибудь мы точно соберем, надо только решить кого. В этом случае ответ будет зависеть от того, равны ли оставшиеся две палочки. Весь алгоритм получается такой:
Найти число, встречающееся не менее четырех раз.
Если такого числа нет, то ответ — "Alien"
Иначе надо удалить четыре вхождения этого числа из входного массива.
Если два оставшихся числа равны, то ответ — "Elephant", а иначе — "Bear".
Вместо того, чтобы искать число встречающееся четыре или более раз, можно было просто отсортироваться входной массив, взять третье или четвертое число и проверить, встречается ли оно четыре раза.
Авторское решение: 7977022
Так как ограничения в задаче очень маленькие, можно было заняться и перебором. Перебрать можно все возможные значения длин для ног, головы и тела. Если взять эти числа (ноги — четыре раза), и получится такой же набор, как во входных данных, то ответ найден. Если для всех вариантов длин они не совпали с изначальным массивом, то ответ — "Alien". Хотя в этой задаче перебор получается не проще основного решения.
Решение с перебором: 7975645
Вообще вроде участники допускали два типа ошибок в этой задаче:
Не учли, что ноги могут быть той же длины, что и голова или тело. Мы учли, что такое непонимание может быть и специально добавили это уточнение в условие. И все равно кто-то напоролся на это.
Были так же решения, в которых числа в изначальном массиве сортировались, а потом проверялись сравнивались числа на определенных позициях. Многие запутались в том, какие же числа сравнивать. Правильно сделать это можно было так:
// 0-индексация, массив уже должен быть отсортирован
if (l[0] == l[3]) cout << (l[4] == l[5] ? "Elephant" : "Bear");
else if (l[1] == l[4]) cout << "Bear";
else if (l[2] == l[5]) cout << (l[0] == l[1] ? "Elephant" : "Bear");
else cout << "Alien";
Такое решение: 7977214
Хоть это решение и короче основного, но в нем есть широкий простор для ошибок, да и подумать немного приходится, поэтому я бы предпочел писать решение выше.
Надеюсь, картинки вам понравились!
471B - МУХ и важные дела
Надо проверить можно ли составить три различные перестановки индексов массива, так чтобы элементы, соответствующие этим индексам получились взятыми в неубывающем порядке. Так как первая часть вопроса сводится к тому, есть ли три таких перестановки, то некоторые участники начали прямо считать количество перестановок, удовлетворяющих условию отсортированности. Этого делать не стоит, так как количество перестановок может легко переполнить и int и long. Часть решений на этом упала.
Можно пойти с другой стороны. Допустим вы уже собрали одну перестановку, идущую в ответ. Тогда в изначальном массиве вы можете найти два равных элемента, переставить их в перестановке и получить вторую перестановку. Сделав это еще раз, вы получите третью перестановку. То есть для наличия ответа достаточно найти две пары чисел, которые можно переставить. При этом даже можно, чтобы одно число в этих двух парах общим, главное чтобы не полностью пары были одинаковые. Найти две такие пары чисел можно в один проход массиву, если его предварительно отсортировать. Тогда нам просто надо проверить равно ли текущее число предыдущему, и если да, то мы нашли два элемента, которые можно поменять местами.
Полностью алгоритм таков:
Создадим новый массив пар (tuples) но основе исходного массива. Первым элементом пары будет значение элемента, вторым — его индекс. Использование пар во многих языках программирования даст нам возможность легко отсортировать массив по значению (первому элементу пары).
Сортируем массив по значению.
Проходим по массиву и ищем элементы, которые можно поменять местами. Пары можно поменять местами, если их первые члены равны. Запоминаем индексы таких пар для обмена. Если нашли две пары индексов для обдмена, то из цикла можно уже выйти, хотя можно и дойти до конца.
Проверяем сколько пар элементов мы нашли, которые можно поменять местами. Если меньше двух, то ответа нет.
В противном случае ответ существует. Тогда выводим изначальную перестановку, потом меняем местами первые два элемента, чьи индексы мы запомнили на третьем шаге, выводим полученную перестановку, переставляем местами еще два элемента и выводим последний раз получившуюся перестановку.
Авторское решение: 7977528
471C - МУХ и карточные домики
Карточный домик. В этой задаче требовалось заняться немного математикой, правда совсем чуть-чуть. Давайте сначала посчитаем сколько карт нам потребуется для создания одного этажа с R комнатами:
C = Cкомнаты + Cпотолок = 2·R + (R - 1) = 3·R - 1
А для постройки дома из F этажей с Ri комнат на i-м этаже необходимое количество карт составит:
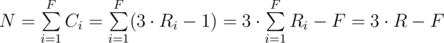
где R — общее количество комнат в домике.
Тут уже можно заметить важное свойство — в правильном домике остаток N + F должно делиться на 3 нацело. То есть если вы нашли каким-то образом интервал возможных значений высот домиков, то в этом интервале в ответ пойдет только каждое третье значение высоты, остальные высоты будут давать ненулевой остаток.
Теперь давайте выясним какой максимальной высоты может быть домик из N карт. Для того, чтобы построить максимально высокий дом при ограниченном количчестве карт, очевидно нам надо на каждый этаж тратить как можно меньше карт. Но у нас есть ограничение, что количество комнат на каждом этаже должно быть меньше, чем на этаже ниже. Получается, что для постройки дома максимальной высоты стратегия должна быть такой: мы ставим одну комнату на самом верхнем этаже, две комнаты — на этаже под ним, потом три комнаты, и так далее. Количество карт, необходимое для строительства такого дома, составит:
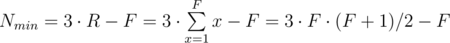
Это минимальное количество карт, необходимое для постройки дома из F этажей. Из этого уравнения мы можем посчитать максимальную высоту дома, который мы можем построить из не более, чем N карт, достаточно просто найти максимальное F которое дает Nmin < = N. Математики могли бы решить это квадратное уравнение руками, а у программистов два варианта:
Проверить все возможные значения F пока Nmin не превысит N. Так как Nmin растет пропорционально F2, то нам понадобится проверить не более
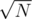 чисел. Так мы получим решение с временной сложностью
чисел. Так мы получим решение с временной сложностью 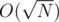 , что вполне укладывается в лимит по времени.
, что вполне укладывается в лимит по времени.Второй вариант — сделать двоичный поиск. Если искать это максимальное количество этажей двоичным поиском, то сложность алгоритма будет уже O(logN). Это было мое изначально задумываемое решение, но потом решили, что и решения за корень пусть проходят.
Теперь, когда мы знаем теоретически максимальное количество этажей в доме, нам может понадобиться немного скорректировать это число в связи с теми рассуждениями об остатке от деления на 3, которые мы делали выше. Для этого вам, возможно, придется уменьшить максимальную высоту дома на 1 или 2. Опять же из тех рассуждений про остаток мы получаем, что начиная с этого количество этажей каждое третье число вниз будет годиться в ответ, надо их просто посчитать. Посчитать можно, перебрав их (опять вернемся к 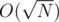 решению), или просто использовав формулу:
решению), или просто использовав формулу:
ans = (Fmax + 3 - 1) / 3 (integer division)
Кажется все, ну и не забывайте везде использовать 64-битные числа в этой задаче.
Авторское O(logN) решение: 7977863
Авторское 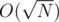 решение: 7977888
решение: 7977888
471D - МУХ и стенки из кубиков
В этой задаче нам даны два массив целых чисел и надо найти, сколько раз второй массив встречается в первом как подмассив, если мы можем предварительно добавить произвольную константу ко всем элементам второго массива. Назовем эти массивы a и b. Как многие участники заметили или знали заранее, эту задачу можно просто решить если перейти к массивам разниц вот так:
aDiffi = ai - ai + 1 (для i = = 0..n - 1)
Проделаем это с обоими входными массивами, тогда мы получим два новых массива, содержащих на один элемент меньше изначальных. А в новых массивах изначальная задача сводится просто к поиску подстроки (пусть и с большим алфавитом) — мы будем искать строку bDiff в строке aDiff. Эту задачу можно решить многими способами и структурами данных — берите какая вам ближе. Изначально предполагалось требовать решение за линейное время, но потом решили сделать ограничения помягче, вдруг кто суффиксный массив за логарифм захочет сдать. Суффиксных массивов я у участников не видел, но квадратичные решения некоторые засылали :-)
За линейное время задачу можно решить, используя Z-функцию строки или алгоритм Крута-Морриса-Пратта. Я написал так же решение с суффиксным массивом, но оно заменто тяжелее пишется, чем линейные решения.
В этой задаче есть один случай, который стоит учесть отдельно — когда стенка Хораса состоит из только одной башенки, тогда он в любой башенки стенки медведей может увидеть слона и ответом будет n. Хотя для некоторых алгоритмов это можно даже и не учитывать отдельно, если считать, что пустая строка совпадает находится в заданной строке в любой позиции. Еще некоторые участники пытались использовать настоящие строки и приводили разностные массивы к char. Это не работает, так как диапазон значений char гораздо меньше диапазона значений в задаче, и такое решение легко можно взломать.
Я не думал, что переход к разностным массивам будет настолько очевидным решением, поэтому не ожидал, что эту задачу решат так много людей и так быстро.
Авторское решение с Z-функцией O(n + w) : 7978022
Авторское мясо с суффиксным массивом O((n + w)·log(n + w)): 7978033
471E - МУХ и много-много отрезков
Нам дан набор горизонтальных и вертикальных линий, надо стерить некоторые части линий или линии целиком, чтобы оставшиеся линии образовывали единую фигуру без циклов.
Для начала давайте рассмотрим решение упрощенной версии этой задачи, которое не убирает циклы и работает за N2. Для такого решения нам достаточно использовть систему непересекающихся множеств (СНМ, DSU), в нее мы кладем все наши линии и начинаем объеденить линии, которые пересекаются. Так же наша СНМ должна считать сумму длин соединенных отрезков, изначально для каждого отрезка мы указываем его длину, а потом СНМ должна при объединении пересчитывать это значение. Так как у нас может быть вплоть до N2 / 4 пересечений между линиями, то мы получили квадратичное решение.
Теперь давайте избавимся от циклов. Для этого мы можем модифицировать предыдущее решение в том месте, где оно объединяет множества в СНМ в случае пересечения отрезков. Стандартная СНМ ничего не делает если объединяемые множества и так совпадают, нам же надо поменять это поведение и в случае попытки объедения множества с самим собой мы будем уменьшать значение суммы длин отрезков в этом множестве на единицу. С точки зрения задачи таким образом мы стираем некоторый единичный отрезок в точке пересечения двух отрезков, таким образом мы избавляемся от цикла. Теперь у нас уже есть правильное решение, но оно не пройдет по времени.
Теперь надо это решение ускорить. В худшем случае мы всегда будем иметь N2 / 4 пересечений отерзков, поэтому очевидно, что для ускорения решения нам надо отказаться от обработки пересечений по одному. Для начала давайте перейдем от рассмотрения пересечений в произвольном порядке к использованию заметающей прямой. Таким образом мы будем рассматривать все пересечения слева направо, например.
В этом случае понятно, что код, который будет отвечать за пересечения — это код, добавляющий вертикальные линии, поэтому давайте разберемся с этим получше. Допустим мы добавляем вертикальную линии с координатами (x, y1, x, y2), так же можем предположить, что у нас есть некоторый набор горизонтальных линий, проходящих через вертикальную прямую с координатой x, мы поддерживаем этот набор горизонтальных линий по ходу работы заметающей прямой. Итак мы добавляем вертикальную линии, которая, допустим, пересекается с n горизонтальными линиями. Из этих n линий некоторые идущие подряд линии могут уже принадлежать одному множеству в СНМ, в таком случае обрабатывать отдельно каждое из этих пересечений нет никакого смысла, достаточно обработать одно из них и перейти к следующему набору линий, принадлежащему другому множеству в СНМ. И в этом и заключается основная идея в этой задаче — вместо того, чтобы хранить горизонтальные линии по одной, мы можем хранить их блоками, где каждый блок принадлежит некоторому конкретному множеству в СНМ и покрывает некоторый интервал вдоль y координаты.
Класс для этого блока выглядит так:
struct chunk{
int top, bottom; // координаты начала и конца интервала, который покрывается данным блоком
int id; // идентификатор множества, которому принадлежит данный блок, в СНМ
};
Нам понадобится некоторая структура данных, которая будет позволять добавлять/удалять эти блоки и находить блок на нужной высоте. Все эти операции мы можем делать за логарифмическое время, используя treap или STL map.
Посмотрим теперь подробнее на то, как это будет работать и почему это будет работать достаточн быстро. В процессе работы заметающей прямой мы будем обрабатывать три типа событий (перечислены в порядке приоритета их обработки) — начало новой горизонтальной прямой, рисование вертикальной прямой, конец горизонтальной прямой. Первая и третья операция каким-то образом меняет наши текущие блоки, вторая операция использует данные о блоках и обрабатывает пересечения. Рассмотрим каждую из операций:
начало горизонтальной линии. В этом случае нам надо добавить еще один блок, чей интервал будет состоять пока из одной точки. Может получиться, что данная прямая будет проходить через интервл, уже занятый каким-то блоком, тогда тот блок надо разбить на два блока — выше горизонтального отрезка и ниже его. То есть, в ходе обработки этого события мы создадим максимум два блока. Это можно сделать за некоторое константное время обращений к нашей стуктуре данных с блоками, поэтому итоговоя временная сложность данной операции — O(logN). Стоит заметить, что эта операция — это будет единственное место, где мы будет создавать новые блоки. Количество вызовов данной операции ограничено N, поэтому в сумме за время работы мы можем получить не более 2·N блоков.
вертикальная линия. Здесь мы должны найти все блоки, с которыми пересечется вертикальная линия, и объеденить их. Искать блоки будем по одному сверху вниз — находим первый блок, потом второй, если второй нашелся, то объединяем их (и сами блоки, и их множества в СНМ) и ищем третий, и так далее. Такой подход гарантирует, что когда блоки для объединения закончатся, то мы потратим на это не больше O(logN) времени. Объединяя два блока мы также потратим O(logN) времени на одно объединение, одна вертикальная линия в худшем случае может пересечь n горизонтальных линий, что даст суммарное время обработки уже O(NlogN). Но несмотря на то, что одна конкретная операция такого типа может работать O(NlogN) времени, мы можем показать, что все операции такого типа в сумме так же будут работать O(NlogN), потому что всего за время работы программы у нас будет создано не более 2·N блоков, как мы показали выше, а каждая операция объединения блоков, уменьшает их количество на единицу. Такой вот амортизационный анализ получился. Еще раз повторю, временная сложность обработки всех операций второго типа составила O(NlogN)
Так же тут есть несколько других деталей, которые нам надо учесть. Например, нам все еще надо избегать возникновения циклов. Поля этого блога довольно узки, чтобы вместить доказательство полностью, но вот эта формула вроде дает правильную поправку, которую нужно внести, когда объединяешь несколько блоков вертикальной линией, идущей от y1 до y2:
d = y2 - y1 - (Nintersections - 1) + Ndistinctsets - 1
where d — поправка, которую нужно внести к сумме длин отрезков получившегося блока в СНМ
Nintersections — количество горизонтальных линий, с которыми пересеклась вертикальная линия. Я находил это значение отдельным деревом отрезков за O(logN)
Ndistinctsets — количество различных множеств, чьи блоки были объеденены вертикальным отрезком, их надо считать по мере объеденения блоков
Таким образом можно правильно корректировать значение суммы длин оставшихся отрезков, чтобы избегать возникновения циклов, при этом опять же нет необходимости рассматривать каждое пересечение по одному. Есть еще одна деталь, которую стоит проговорить, — может получиться, что вертикальная линия, попала в некоторый блок, но не пересеклась там ни с одной горизонтальной линией, в таком случае эту вертикальную линию надо пропустить, как если бы она вообще не попала ни в какой блок.
конец горизонтальной линии. Наконец мы досюда добрались и тут вроде все просто. Когда заканчивается какая-нибудь горизонтальная линия нам может понадобиться обновить наш блоки. Всего может быть три случая:
a. Эта линия всего одна в блоке — удаляем блок полностью.
b. Эта линия является каким-либо краем интервала блока — надо удалить эту линию и найти новый край интервала, я это делал с помощью того же дерева отрезка, которое я упоминал выше.
c. Линия лежит внутри интервала некоторого блока — тогда блоки обновлять не надо.
Ну вот вроде и все, таким образом мы получаем O(NlogN) решение.
Авторское решение: 7978166 (в коде структура данных с блоками называется 'linked_list', я думал изначально, что там будет связный список, но постепенно концепция поменялась, а название осталось).











Appreciative Editorial.................
Thanks for nice contest and editorial :D
Regard to problem C, I think it can be solved in O(1), here is my solution
care to explain this solution?
u can make min
3 - n%3floors. find maximum. letc[i]be number of houses on i-th floor(numeration from 1). letkbe number of floors. notice that(c[1] + c[2] + ... + c[k]) * 3 - k = norc[1] + c[2] + ... + c[k] = (n - k) / 3. min value of sum in the left part isk * (k + 1) / 2. so, whenk * (k + 1) / 2 <= (n - k) / 3u can build k floors. solve it and u'll find maxku can use. ans is(kmax - kmin + 3) / 3There are wrong signs in
c[1] + c[2] + ... + c[k] = (n - k) / 3andk * (k + 1) / 2 <= (n - k) / 3. The '-' should be replaced by '+'.yeah, c is O(1) task 7964152. how hasn't author noticed that?
"Mathematicians would probably solve the quadratic inequation, programmers have two options" pretty much sums up that author indeed noticed a O(1) solution.
sorry, haven't noticed that
With large N,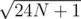 will lose precision, so it's also a good thing that N ≤ 1012 fits the solution in double types. (And consequently for large N, I call that
will lose precision, so it's also a good thing that N ≤ 1012 fits the solution in double types. (And consequently for large N, I call that 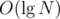 solution too as finding the square root is not trivial; binary searching the square root is reasonable.)
solution too as finding the square root is not trivial; binary searching the square root is reasonable.)
if u use long double, u'll get enough precision
If you are afraid of losing precision you can always check on integers whether your desired sqrt is correct and in case of failure try +-1.
I mean "for large N" means "for N somewhere around 10100 to 10100000", which is beyond the boundaries of the problem. I just say that it's possible to increase the constraints if people can use arbitrary-precision integers.
After a nice announcement now a nice editorial... :)
Never seen a Div2E this complicated before.
In a previous round written by YuukaKazami, no one solved problem div2-E during the contest. However That problem is not much difficult now, because at that time suffix automaton was first introduced to handle string problems, so no one but the author knows it. And later YuukaKazami admitted that it is a fault, because he didn't know div.2 problems C,D,E must be div.1 A,B,C problems, otherwise it will be D.
But a div.2 only round can have such a difficult problem.. This round has set up a new record :p
Thanks for readable solution codes .
Серьёзно, блин?) Даже я бы скорее автоматом сдал. Кстати... 7980862
Ну вот обязательно надо было процитировать мой "суффЕксный массив"? :-)
Геральд четко сказал, что в Див. 2 надо дать возможность зайти всему, кроме тупняка. Ну и вообще, я первый раз суффмассив использовал, жалко чтоли?
why this code get WA? 7967749
Isn't that obvious that if you use hashes you can get WA because of the way the hash works? Hash of one sequence can be equal to hash of another one, but the sequences itself could be different. You just got unlucky here. ;) Consider reading about Anti-hash test and try solving D with Z-function, it's not that hard.
The contest was great :) But I wonder, how have you done that all my hashings algorithms with different keys are failing at 25th test?![submission:7982970][submission:7982847][submission:7968344] How did you create this test?! Thank you!
Hi, 25th test was added based on riadwaw's hack, you can see the generator here, as far as I know it is based on this anti-hash article here, maybe not, you can probably ask him to clarify.
Did anyone else get this problem AC-ed using hash? I did :)
Yeah, that's exactly this test
Lol, E seems so easy now ; d. I'm surprised that nobody came up with this (I was stuck at implementing KMP XD, though either way I didn't have idea after the contest), though it may be not that nice in implementation. There is just this idea with chunks, everything else seems pretty standard ("everyone is clever after hearing solution" :>). Indeed, if it was hard for red coders, it was surely not suitable for Div2, but seeing the results I was expecting really hardcore one :P (my friend even suggested flawed authors' solution xD).
Nice problem and solution, congrats! And +1 for "This margin is too narrow to contain the proof" :>!
Well, the overall idea of these chunks is simple, especially if you would be told to use them then the problem is not that hard, that's true. But coming up with this idea is not so easy, I think especially because you cant't just come up with it, you need to get some idea why it would actually make the entire solution fast enough. And the implementation is not that nice, you're right. Even though you will probably get everything you need to do as soon as you get the idea of chunks, but there are several places you can introduce bugs easily. Both me and Gerald spent some time debugging our solutions and we were in much better situation than participants, cause we had test data and slow reference solution and a lot of time, that situation should have been ringing a bell in my head. Believe me, there is nobody more disappointed in this situation than me, because I gave to Div. 2 a problem which turned out to be good for Div. 1.
Замечательный раунд, большое спасибо автору marat.snowbear
What would happen for problem B, If we had P animals instead of only 3? How could we solve it?
The number was chosen especially because you can do that easily with 2 swaps and you don't need to care whether there is some element common for both swaps or not. For example if you ask for 4 permutations it will be different because in the case when you have 3 equal elements you might have to swap first and second, then second and third and then first and second again. That makes it more complicated and less suitable for Div. 2 B. Also in your problem you probably won't be able to ask for large P values, because participant will have to output a lot of numbers and many solutions will time out because of output only, which is not good.
The solution for your problem is still not that complicated though, you will need to break the input into groups of equal elements, let's say that sizes of those groups will be s1, s2, ..., sn. Then the total number of permutations you can achieve is simply s1!·s2!·...·sn!. This gives you an idea whether you can provide P permutations or not. Then you need to provide those, since it grows as factorial of the size of the group then for let's say P < = 1000 it will be enough for you to do permutations within some group of 7 elements because 7! = 5040, so you won't even need to complex things to get next permutation, also in C++ you might find method next_permutation useful for that.
Yeah next_permutation worked for me as marat.snowbear said.
I coded it in the general way as you asked.
Here it goes 7977257
Just need to make few changes in do..while loop
Hope that helps :)
Nice Editorial...****
Thanks for the problem E. It was really nice :)
From Problem C Editorial:
"This means that if you have found some minimum value of floors somehow and you found maximum possible number of floors in the house, then within that interval only every third number will be a part of the solution, the rest of the numbers will give a non-zero remainder in the equation above."
Can anyone explain this more please?
marat.snowbear, can you help me please?
Forget about minimum and maximum, I was just trying to say that from all integer numbers, every third will satisfy the condition that the remainder will be zero. Try it yourself, choose some n and see which numbers x give (n + x)mod3 equal to 0.
Good, I got the idea using the sqrt approach.
For the idea using binary search, where did the formulae that counts the third numbers ans = (Fmax + 3 - 1) / 3 come from?
Hmm, I don't know, I think this is kind of formulae people deduce themselves. This is the formulae which gives you an answer to this question:
In this case the answer would be (n + p - 1) / p.
Well explained editorial, a rarity in codeforces.
an other solution for problem c it gives O(1) cin>>n; a=sqrt(1+24*n)-1; a/=6; if (n%3==1) a+=1; if (n%3==2) a+=2; cout<<a/3;
can you explain it ?!
can anybody help me and tell why my code is showing compilation error. On my system it is working fine. Here is my submission link
you need to include cstdlib on the top of the code.
problem D can be easily solved in nlogn using a good hashing function similar to polynomial string hashing, having the multiplying factor as a prime number over 10^9, say 1000000007, and taking modulo over two distinct prime numbers (also greater than 10^9), so that there is very less chance of collision. here is my solution: 10454545
Please, explain me why (N+F)%3 must be 0! (Problem C)