Есть такая головоломка — я на неё давно в книжке М.Гарднера наткнулся: даны квадраты, разбитые на 4 треугольных сектора каждый — сектора выкрашенны в 3 разных цвета. Всего различных квадратов получается 24 и если покумекать, из них можно сложить прямоугольник 6*4, так что:
- вся граница прямоугольника состоит из треугольных секторов одного цвета;
- внутри квадраты касающиеся сторонами должны иметь на этих сторонах одноцветные треугольники.
Извиняюсь за косноязыкость, вот так выглядит типовое решение, чтоб понятнее было:
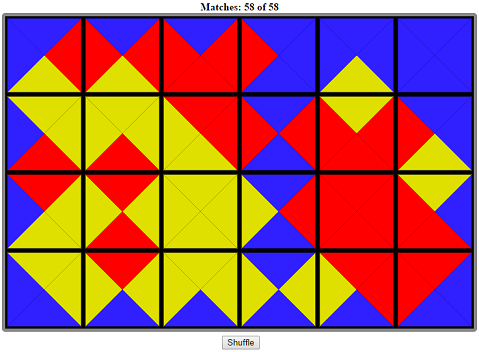
Онлайн можно попробовать повертеть головоломку на этой страничке.
Автор видимо Александр МакМагон.
Хотя решение с полпинка найти нелегко, их на самом деле много. Гарднер упоминает что один из его читателей вывел аналитически — а второй с помощью ЭВМ число около 12 тысяч.
И вот стало мне любопытно — как программно это дело посчитать (чтобы понять можно ли из этого какую-то задачу придумать).
Т.е. можно наверное посидеть какое-то время над головоломкой, определить что некоторые из квадратов могут занимать только такие-то места и потом перебор с ограничениями писать. Но это выглядит сурово.
И вопрос в том — существуют ли какие-то более легкие способы ограничить перебор или что-то в этом духе.
Кажется, должен без проблем зайти перебор "по спирали": начиная с угла и заканчивая серединой.
Интересно, попробую!
Хотя тут такое — нам нужно подобрать
23квадрата (кроме углового), и если на место каждого будет в среднем2претендента то это выльется в2^23, т.е. по порядку мильон... А если в среднем по3— то уже около9e+10.Впрочем "среднее" трудно угадать. Для каждого квадрата будут известны как минимум 2 стороны, значит максимальное число кандидатов
9— но это конечно только в начале... Впрочем написав код я смогу как минимум оценить количество кандидатов на каждом уровне...Я написал перебор еще 6 октября, но до того, чтобы его отдебажить, руки дошли только сейчас. В-общем, вот код. К сожалению, работает весьма медленно (примерно 9 минут для каждого из внешних цветов на ноуте с процессором Core i7-4710HQ).
Итого получается ровно 319872 варианта. Если учесть симметрию (6 перестановок трех цветов и 4 различных способа отразить игровое поле), то останется 13328 вариантов.
UPD. Все намного интереснее. Вбив в гугл запрос "Martin Gardner 13328", я натолкнулся на эту книгу и узнал, что 13328 различных решений были найдены еще в 1977 году. Потом я нашел и русскую версию, но в ней эта цифра не упоминается.
It seems quite easy to me. The outer triangles can have one colour and the innner ones can be paired with each other in a bijection. Each pair can be of any of the 3 colours; there are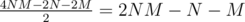
of them, so there are 32NM - N - M + 1 ways. That's in case there don't have to be exactly 3 colours in each square (which is supported by your example solution).But does your solution regard that the same squares could not be used twice? — puzzle consists of 24 unique squares...
I just noticed while playing the game. It seemed too easy, I felt that I'm missing something, just didn't know what :D
LOL, after ur edit i noticed that u can't
strikethroughstuff written usingUnable to parse markup [type=CF_TEX]
. :Dwhew, this puzzle would be so much easier to solve if we could keep some blocks outside the board to avoid them from distracting us from the blocks which we are currently placing!
anyway, i found a different solution than urs.
my bad — I just created this small script to examine the problem myself (instead of making it of paper etc) — however anyone can easily fork it and modify...
there seems to be many of them. Yesterday I've found one which, according to my wife's opinion, looked like a cat.
There is an interesting feature of solutions — "diamonds" — i.e. pairs of same-color triangles forming romboid surrounded by other colors. There should be some min and max for amount of these "diamonds" — but I do not remember them...
UPD your solution looks like inversion of mine — are you sure you weren't cheating? :)
cheated by simply "copy-pasting" ur solution? no.
noticed a pattern with ur solution before starting to solve the puzzle? yes.
still, i have solved it again just to satisfy you. :D
Tada!
Four diamonds here — three red and one yellow. Looks like close to minimum!
I only see 2 red ones. Same with your solution. Hypothesis: there are always 3 diamonds / 3 of the colours that are not on the border.
Funny, now I see 3 red and 3 yellow:
Mine has 4 red, 3 yellow and 2 blue ones. I found the book — it states the maximum is 13.
Oh, that kind of diamond! I assumed it'd be 8-triangle ones, because the numbers were closer...
So the goal is basically to get colours to bigger/fewer connected components.
It looks like left solution has
9isolated "diamonds", while left only6. I myself could not make more than9also, though probably it is not an upper limit...Думаю Meet-In-The-Middle пойдёт чтобы посчитать на одном компе за сутки.
1. Перебираем цвет границы. 3
2. Перебираем маску цветов двух соседних столбцов в середине поля. 3^4
3. Перебираем множество квадратов слева. C(24, 12)
4. Решение задачи слева и справа перебором.
[1] * [2] * [3] = 3 * 81 * 2704156 = 657 109 908
Вопрос как быстро перебор будет справляться с задачей
для поля квадратов 3 X 4 с известным цветом границы и области касания.
Думаю его можно реализовать довольно быстро (можно ещё раз применить подобный Meet-In-The-Middle)
для 3 x 4 можно дп по изломаному профилю + битовая маска использованных квадратов 3^4 * 2^12 = 331776. Итого 218 013 296 836 608. Многовато, если в решении подзадачи 3^4 будет мало отсечений. Вообще всюду отсечения нужны, уже на этапе "3. Перебираем множество квадратов слева. C(24, 12)" можно понять, что маловато цветов для границы.
самое оптимальное что я придумал, это
1. перебрать цвет границы для прямоуголььника 4 x 6.
2. перебрать цвет контактирующих участков внутри прямоугольника 3 x 4 (9+8)
3. перебрать 4 цвета между серединными столбцами
итого 3^(1+9+8+4=22)=31 381 059 609 (без учета отсечений)
После этого левые 12 квадратов полностью определены. сортируем их. определяем есть ли у нас такое подмножество квадратов. И здесь хитрый Meet-In-The-Middle, который запоминает для каждого из C(24, 12)=2 704 156 подмножеств квадратов сколько раз оно встречалось. PS: забыл про цвет границы, он тоже важен. ну тогда будет массив(или мап) из 2 704 156 * 81 чисел, по которому затем нужно будет построить ответ
Вы учтите, что цвета симметричны, а значит цвет границы и ещё один цвет можно просто зафиксировать.
Ты уверен, что они симметричны? Мне показалось что некоторых квадратов не хватает, хотя могу ошибаться. Всмысле если применить к цветам всех квадратов перестановку (3, 1, 2), то мы получим другое множество квадратов. Могу ошибаться.