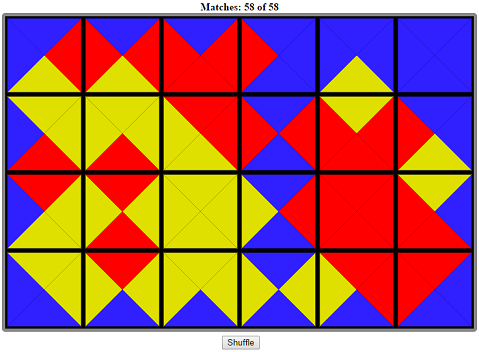
M.Gardner in some of his books describes the puzzle: there is a set of squares, each divided into 4 triangular sectors — and these triangles are painted in 3 colors. There exists 24 different squares and it is possible to arrange them into 6*4 rectangle, so that:
- all triangles touching the border of the rectangle have the same color;
- each two neighbor squares have triangles of the same color on their common edge.
To make it more clear, here is an illustration of the solution:
You can try to play with the puzzle at this page.
Gardner told that the author is Percy Alexander MacMahon.
Though it is not easy to find solution at once, there exist many of them. Gardner wrote that some of his readers counted analytically and other with the help of computer the number about 12 thousands.
This phrase made me curious how to write a program to count these solutions.
I have no other idea except to play with puzzle and find out some "laws" about placing some specific squares — and then to write brute-force limited with these laws. But it looks complicated.
So my question is whether there exist easier methods to limit the brute-force or some more cunning approaches?











It seems quite easy to me. The outer triangles can have one colour and the innner ones can be paired with each other in a bijection. Each pair can be of any of the 3 colours; there are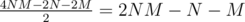 of them, so there are 32NM - N - M + 1 ways. That's in case there don't have to be exactly 3 colours in each square (which is supported by your example solution).
of them, so there are 32NM - N - M + 1 ways. That's in case there don't have to be exactly 3 colours in each square (which is supported by your example solution).But does your solution regard that the same squares could not be used twice? — puzzle consists of 24 unique squares...
I just noticed while playing the game. It seemed too easy, I felt that I'm missing something, just didn't know what :D
LOL, after ur edit i noticed that u can't
strikethroughstuff written usingUnable to parse markup [type=CF_TEX]
. :Dwhew, this puzzle would be so much easier to solve if we could keep some blocks outside the board to avoid them from distracting us from the blocks which we are currently placing!
anyway, i found a different solution than urs.
my bad — I just created this small script to examine the problem myself (instead of making it of paper etc) — however anyone can easily fork it and modify...
there seems to be many of them. Yesterday I've found one which, according to my wife's opinion, looked like a cat.
There is an interesting feature of solutions — "diamonds" — i.e. pairs of same-color triangles forming romboid surrounded by other colors. There should be some min and max for amount of these "diamonds" — but I do not remember them...
UPD your solution looks like inversion of mine — are you sure you weren't cheating? :)
cheated by simply "copy-pasting" ur solution? no.
noticed a pattern with ur solution before starting to solve the puzzle? yes.
still, i have solved it again just to satisfy you. :D
Tada!
Four diamonds here — three red and one yellow. Looks like close to minimum!
I only see 2 red ones. Same with your solution. Hypothesis: there are always 3 diamonds / 3 of the colours that are not on the border.
Funny, now I see 3 red and 3 yellow:
Mine has 4 red, 3 yellow and 2 blue ones. I found the book — it states the maximum is 13.
Oh, that kind of diamond! I assumed it'd be 8-triangle ones, because the numbers were closer...
So the goal is basically to get colours to bigger/fewer connected components.