MikeMirzayanov's blog

2014-2015 CT S02E04: Codeforces Trainings Season 2 Episode 4
By MikeMirzayanov, 10 years ago, In English

Welcome to 2014-2015 CT S02E04: Codeforces Trainings Season 2 Episode 4 (US College Rockethon 2014 + COCI 2008-5 + GCJ Finals 2008 C). The training duration is 4.30 hours. It is opened for teams as well as for individual participants. After the end you may use the practice mode to complete problem solving. Also it will be availible as a virtual contest for whose of you who can't take part today. Please, do not cheat. Only fair play!

It is possible that the problems will be too easy for some participants, it is possible that we will add some problems.

Good luck!

  • Vote: I like it
  • +50
  • Vote: I do not like it

Comments Comments (39)
| Write comment?
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Haha I like the picture xD

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

GL & HF !

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

:\ It would have been nice to know about the gym contest/training in advance. Can you guys post this at least a day earlier to the start of contest?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Look at Gym tab more often, there was announcement 2 days ago.

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How was problem A to be solved?

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Look at this problems in different way: You've got Mi man and Wi woman "fighting" for Si shoelaces. Greedy algorithms does the trick. Firstly, give all shoelaces to woman (because you're gentleman) and take back and give shoelaces to man until there are more woman with shoelaces. Don't do it one by one, but count how many you should take back for every color.

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Tricky test for G?

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Dunno, the straightforward "subtract N - i from non-negative sum, add N - i to negative sum" for all i from 1 to N - 1 worked for me...

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      He asks about problem G, not B.

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      BTW: It was, indeed :D

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      Could you prove your solution?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Probably some induction, that all negative sums after adding N - 1 will yield a sum that can be constructed with N - 1 elements, similarly for positive sums...

        Note that parity of the sum only depends on N.

        → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Just do a few examples by hand. With length 1 you can do (+1, -1), length 2 can do (+3, +1, -1, -3), length 3 gives (+6, +4, +2, 0, -2, -4, -6) and so on. Clearly if you are within the right bounds and parity, you can always find the solution by greedily keeping as close to 0 as possible.

        → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I solved it with this solution: for every i from 2 to N we see whether the a[i-1] less than S/(N-i). If it is true, a[i]=a[i-1]+1, else a[i]=a[i-1]-1. Then S=S-a[i]. If i=N and S!=0 there is no answer.

      I seriously doubted if it would work, but it was accepted. Maybe, there are countertests for this solution?

      → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

how to solve I and J? These tasks made me confused!

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    I: there's a DAG with at most 2 edges from each vertex; if a vertex is (position, last jump direction), you can make "dummy jumps" whose cost depends on whether the direction of the last and next jump are the same

    J: trie, offline (add the dictionary into the trie); in particular, all answers will be either the sum of LCP with all strings or the sum of LCP of s[i] with s[j < i]

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      There are also lot of ways to solve J online — for example, by storing all entrances of every vertex of trie in some vector and using bin.search. And my first thought was about persistent trie — probably because i was solving CF#276 short time ago:)

      BTW, offline solution actually looks easier:)

      → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it +21 Vote: I do not like it

My codes: A B C E G H I J K

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    can you put the d and f solution,thanks

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      No, because I haven't solved them yet. When I do, I'll post them :D

      → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you explain solution to E? I could only understand up to line 43

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      The main point is that relative order of elements doesn't change, so the value by which the sum changes when an element is incremented doesn't depend on the other chosen elements.

      → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

how to solve problem d

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You can calculate new coordinates of your raplaces, so you handle requests from the end, calculate on each step new coordinates. It's work with O(m) complexity.

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    In problem D , the rotation and reflection (Mirror) can be done in O(1). In these cases only the starting position for row , starting position for column , direction of row , direction of column changes.Also in case of rotation the board inverts . The row becomes column and columns became rows( Something like that !!!). If you handle this cases and just simulate accordingly for replacing your work is done.

    My Code.

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can u please post the editorials? Would be of great help...

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone please explain G.

Xellos's solution and explanation seem like magic to me. It would be nice if someone could elaborate on the idea.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    G can be converted to this problem. Put + (or -) in proper way to solve this equation: (n-1) +/- (n-2) +/- (n-3) +/- ... +/- 1 = s

    → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it +1 Vote: I do not like it

    What is the max sum possible : (n*(n-1))/2 when you place 0,1,2,...n-1 : now consider some place x(0<=x<=n-2) after which instead of increasing you decrease, then 0,1,..x,x-1,x,x+1,... : this makes the sum decrease by 2*(n-x-1). So, the problem can be viewed as decreasing after some positions to achieve required sum. Of course, if abs(sum)>(n*(n-1))/2, then answer is not possible. Because you decrease some multiple of 2, the parity of sum and (n*(n-1))/2 should be same. Now, a greedy approach starting from x=0, current_sum = (n*(n-1))/2, by decreasing the maximum possible allowed, and storing after which indices you have decreased.

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem F was really interesting. What was the intended solution?

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 3   Vote: I like it +20 Vote: I do not like it

    Let me start from the end to give the motivation for the rest. The following formula gives the solution to the problem:

    Let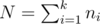 and

    With this formula it is trivial to get an O(k2k) algorithm, and fairly simple to get an O(2k).


    Now the derivation:

    Note: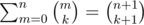


    To count the number finished states, label them by the last station on each track that is on strike. There are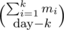 states with each label.




    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Such a strong test cases... My AC solution for problem C (8689388) says IMPOSSIBLE for 

3
100 100 100 100 100 100 100
100 100 100 100 100 100 100
100 100 100 100 100 100 100
100 100 100 80 70 60 100
100 100 100 25 100 50 100
100 100 100 20 30 40 100
100 100 100 10 100 100 100

Of course, correct answer for this case is 

7
7 4
→ Reply