Добро пожаловать на 2014-2015 CT S02E04: Codeforces Trainings Season 2 Episode 4 (US College Rockethon 2014 + COCI 2008-5 + GCJ Finals 2008 C). Продолжительность тренировки — 4 часа 30 минут. Тренировка открыта как для команд, так и для индивидуальных участников. После ее окончания вы можете дорешивать задачи тренировки или поучаствовать в ней виртуально, если не смогли принять участие одновременно со всеми. Пожалуйста, участвуйте в тренировке честно.
Так как это тренировка, то возможно набор задач будет расширен, если для значительного количества участников он окажется простым.
Условия задач будут на английском языке, ведь мы же готовимся к ACM-ICPC!
Удачи!











Haha I like the picture xD
but bugs have only six legs
do bugs have toes ?!
Why "only"? This bug has 2 legs, the rest are hands :D
GL & HF !
:\ It would have been nice to know about the gym contest/training in advance. Can you guys post this at least a day earlier to the start of contest?
Look at Gym tab more often, there was announcement 2 days ago.
How was problem A to be solved?
Look at this problems in different way: You've got Mi man and Wi woman "fighting" for Si shoelaces. Greedy algorithms does the trick. Firstly, give all shoelaces to woman (because you're gentleman) and take back and give shoelaces to man until there are more woman with shoelaces. Don't do it one by one, but count how many you should take back for every color.
Tricky test for G?
Dunno, the straightforward "subtract N - i from non-negative sum, add N - i to negative sum" for all i from 1 to N - 1 worked for me...
He asks about problem G, not B.
Whoops :D
BTW: It was, indeed :D
Could you prove your solution?
Probably some induction, that all negative sums after adding N - 1 will yield a sum that can be constructed with N - 1 elements, similarly for positive sums...
Note that parity of the sum only depends on N.
Just do a few examples by hand. With length 1 you can do (+1, -1), length 2 can do (+3, +1, -1, -3), length 3 gives (+6, +4, +2, 0, -2, -4, -6) and so on. Clearly if you are within the right bounds and parity, you can always find the solution by greedily keeping as close to 0 as possible.
I solved it with this solution: for every i from 2 to N we see whether the
a[i-1]less thanS/(N-i). If it is true,a[i]=a[i-1]+1, elsea[i]=a[i-1]-1. ThenS=S-a[i]. If i=N and S!=0 there is no answer.I seriously doubted if it would work, but it was accepted. Maybe, there are countertests for this solution?
how to solve I and J? These tasks made me confused!
I: there's a DAG with at most 2 edges from each vertex; if a vertex is (position, last jump direction), you can make "dummy jumps" whose cost depends on whether the direction of the last and next jump are the same
J: trie, offline (add the dictionary into the trie); in particular, all answers will be either the sum of LCP with all strings or the sum of LCP of s[i] with s[j < i]
There are also lot of ways to solve J online — for example, by storing all entrances of every vertex of trie in some vector and using bin.search. And my first thought was about persistent trie — probably because i was solving CF#276 short time ago:)
BTW, offline solution actually looks easier:)
My codes: A B C E G H I J K
can you put the d and f solution,thanks
No, because I haven't solved them yet. When I do, I'll post them :D
Can you explain solution to E? I could only understand up to line 43
The main point is that relative order of elements doesn't change, so the value by which the sum changes when an element is incremented doesn't depend on the other chosen elements.
Sorry, I didn't see word "distinct".
How to solve G?
how to solve problem d
You can calculate new coordinates of your raplaces, so you handle requests from the end, calculate on each step new coordinates. It's work with O(m) complexity.
In problem D , the rotation and reflection (Mirror) can be done in O(1). In these cases only the starting position for row , starting position for column , direction of row , direction of column changes.Also in case of rotation the board inverts . The row becomes column and columns became rows( Something like that !!!). If you handle this cases and just simulate accordingly for replacing your work is done.
My Code.
can u please post the editorials? Would be of great help...
Can anyone please explain G.
Xellos's solution and explanation seem like magic to me. It would be nice if someone could elaborate on the idea.
G can be converted to this problem. Put + (or -) in proper way to solve this equation:
(n-1) +/- (n-2) +/- (n-3) +/- ... +/- 1 = sWhat is the max sum possible : (n*(n-1))/2 when you place 0,1,2,...n-1 : now consider some place x(0<=x<=n-2) after which instead of increasing you decrease, then 0,1,..x,x-1,x,x+1,... : this makes the sum decrease by 2*(n-x-1). So, the problem can be viewed as decreasing after some positions to achieve required sum. Of course, if abs(sum)>(n*(n-1))/2, then answer is not possible. Because you decrease some multiple of 2, the parity of sum and (n*(n-1))/2 should be same. Now, a greedy approach starting from x=0, current_sum = (n*(n-1))/2, by decreasing the maximum possible allowed, and storing after which indices you have decreased.
Thanks amitsaharana, very interesting solution indeed.
i used same kind of approach ... if possible can u tell whats wrong with my solution.... http://ideone.com/TWhSUX
Problem F was really interesting. What was the intended solution?
Let me start from the end to give the motivation for the rest. The following formula gives the solution to the problem:
Let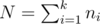 and
and 
With this formula it is trivial to get an O(k2k) algorithm, and fairly simple to get an O(2k).
Now the derivation:
Note: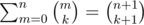
To count the number finished states, label them by the last station on each track that is on strike. There are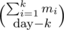 states with each label.
states with each label.
Such a strong test cases... My AC solution for problem C (8689388) says IMPOSSIBLE for
Of course, correct answer for this case is