SRM637 Div1Medium can be solved even if the width of the board is very very large.
There is O(|black cells|) solution.
Let's consider only 8 cells near the edge. There are three(four) cases:
1) There are black cells in both side.
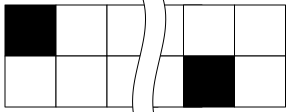
In this case, already result is fixed because the players can not change a parity of the number of turns while the game ends.
2) There are black cells in only one side.

In this case, the first player can win because he can decide a parity by coloring the other side cell black.
3) There is no black cell in both side.

In this case, the player who color a side cell black at the first loses. Hence the winner in the board without 8 side cells wins. You can determine the winner recursively.
0) The width of the board is less than 4.
In this case, it is easy to determine the winner.











Hmm, nice.
I'm curious: what was the reason for the initial systest fail?
My first solution contained a bug and I fixed but it was not updated in the system for some reason. Sorry for that.
I know what you mean, MPSQAS does some weird shit sometimes. I used to save by "save statement -> submit -> save statement -> submit".
Did your buggy solution fail on test case {".", "."}?
No. It was a strange bug so I think nobody took the same mistake with me.
Strictly speaking I think it's not (Black) anyway, because with the given input format you need to locate all black cells which takes O(Width) time anyway.
If they want it to be the intended solution, I don't think changing the input format is impossible though.
I didn't care the input format because it is not essential. (If the width of the board is very large, the input format will be changed.)
Hmmmm, actually there is a more simple O(Blacks) solution for this problem, because of the nice pattern which can be seen in the computed grundy numbers. something like this:
(Suppose we have black cells positions in a vector of integer pairs named
v, sorted by their column numbers)Second player wins if and only if
ansequals zero at the end.