Based on the approach in my previous blog, today, I found an amazing way to calculate large fibonacci numbers (in some modulo). According to part IV of my previous blog, let f(n) be the (n + 1)th fibonacci number, we have two case: n is even and n is odd.
- f(2 * k) = f(k) * f(k) + f(k - 1) * f(k - 1)
- f(2 * k + 1) = f(k) * f(k + 1) + f(k - 1) * f(k)
There are only at most 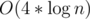 states. I don't like to prove this, but I can ensure it is true by doing some following experiment. Let's divide n into groups by depth, you will realize a special property: Each depths only contains at most 4 values of n.
states. I don't like to prove this, but I can ensure it is true by doing some following experiment. Let's divide n into groups by depth, you will realize a special property: Each depths only contains at most 4 values of n.
call f(1000):
Depth[0] : 1000
Depth[1] : 499 500
Depth[2] : 248 249 250
Depth[3] : 123 124 125
Depth[4] : 60 61 62 63
Depth[5] : 29 30 31 32
Depth[6] : 13 14 15 16
Depth[7] : 5 6 7 8
Depth[8] : 1 2 3 4
Depth[9] : 0 1 2
Depth[10] : 0 1
call f(123123123122):
Depth[0] : 123123123122
Depth[1] : 61561561560 61561561561
Depth[2] : 30780780779 30780780780 30780780781
Depth[3] : 15390390388 15390390389 15390390390 15390390391
Depth[4] : 7695195193 7695195194 7695195195 7695195196
Depth[5] : 3847597595 3847597596 3847597597 3847597598
Depth[6] : 1923798796 1923798797 1923798798 1923798799
Depth[7] : 961899397 961899398 961899399 961899400
Depth[8] : 480949697 480949698 480949699 480949700
Depth[9] : 240474847 240474848 240474849 240474850
Depth[10] : 120237422 120237423 120237424 120237425
Depth[11] : 60118710 60118711 60118712 60118713
Depth[12] : 30059354 30059355 30059356 30059357
Depth[13] : 15029676 15029677 15029678 15029679
Depth[14] : 7514837 7514838 7514839 7514840
Depth[15] : 3757417 3757418 3757419 3757420
Depth[16] : 1878707 1878708 1878709 1878710
Depth[17] : 939352 939353 939354 939355
Depth[18] : 469675 469676 469677 469678
Depth[19] : 234836 234837 234838 234839
Depth[20] : 117417 117418 117419 117420
Depth[21] : 58707 58708 58709 58710
Depth[22] : 29352 29353 29354 29355
Depth[23] : 14675 14676 14677 14678
Depth[24] : 7336 7337 7338 7339
Depth[25] : 3667 3668 3669 3670
Depth[26] : 1832 1833 1834 1835
Depth[27] : 915 916 917 918
Depth[28] : 456 457 458 459
Depth[29] : 227 228 229 230
Depth[30] : 112 113 114 115
Depth[31] : 55 56 57 58
Depth[32] : 26 27 28 29
Depth[33] : 12 13 14 15
Depth[34] : 5 6 7 8
Depth[35] : 1 2 3 4
Depth[36] : 0 1 2
Depth[37] : 0 1
According to the amazing property, we can calculate 1018-th fibonacci number by using little code:
#include <map>
#include <iostream>
using namespace std;
#define long long long
const long M = 1000000007; // modulo
map<long, long> F;
long f(long n) {
if (F.count(n)) return F[n];
long k=n/2;
if (n%2==0) { // n=2*k
return F[n] = (f(k)*f(k) + f(k-1)*f(k-1)) % M;
} else { // n=2*k+1
return F[n] = (f(k)*f(k+1) + f(k-1)*f(k)) % M;
}
}
main(){
long n;
F[0]=F[1]=1;
while (cin >> n)
cout << (n==0 ? 0 : f(n-1)) << endl;
}
The complexity of above code is 
You can reproduce my experiment by using this code.











I did implemented this code before too. Its nice and shorter than Matrix exponentiation. I have found this on wikipedia Fibonacci Numbers.
F[2*n — 1] = F[n]*F[n] + F[n — 1]^2
F[2*n] = (F[n — 1] + F[n + 1])*F[n] = (2*F[n — 1] + F[n])*F[n]
I have a marvellous way to calculate fibonacci number using only TWO lines of code :P
See here.
Did you forget
#include <bits/stdc++.h>?Nice article. I wonder if you can you somehow invent a way to calculate k-inversions faster than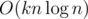 ?
? 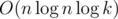 for example.
for example.
I don't understand. What did you mean "k-inversions"?
It's the quantity of sets of indices in permutation i1 < i2 < i3 < ... < ik such that ai1 > ai2 > ai3 > ... > aik. I.e. it's amount of decreasing subsequences of length k in permutation.
i[1] < i[2] < ... < i[k]
a[i[1]] > a[i[2]] > ... > a[i[k]]
(adamant was faster...)
Can you give me some hint for the O(knlogn) approach? I can only solve it up to k = 3 in O(nlogn^2), using BIT 2D.
suppose (i, j) is an inversion and j is a first element of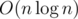 using mergesort
using mergesort
inv[k-1][j](k-1)-inversions. So,inv[k][i] = sum(inv[k-1][j])for all j, you can calculate it inAlthough the observation is interesting, I don't get what relevance it has in the above implementation. I would write pretty much the same code without the realizing that each depth has at max 4 states. Could you please clarify?
I didn't understand you question well. My following answer can be not appropriate.
This such small complexity is unintentional. I expected to find a solution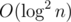 .
.
What I mean to say is at at each of the log(n) levels, there are going to be 4 possible values. But how does that effect the algorithm, what is the use of this information? I have these results: ~~~~~ f(2 * k) = f(k) * f(k) + f(k - 1) * f(k - 1) f(2 * k + 1) = f(k) * f(k + 1) + f(k - 1) * f(k) ~~~~~
Couldn't I just use these 2 results and obtain in logarithmic time?
Well, As I look at it, I might be getting what your point is, so basically if I have calculated f(k), I might very well have lots of required values for f(k-1), and that's what makes the algorithm faster. I suppose this is what you mean to say?
Forgive me but this does not strike me as anything special. It is basically just a poor man's version of the matrix multiplication + exponentiation by squaring anyway (the computed values should be the same). Plus, you are losing the insights from linear algebra, so it will be harder for you to see the solution for less trivial recurrence relations.
Computing Fibonacci numbers using matrix multiplication requires approximately the same amount of code as your approach:
(And finally, the line "#define long long long" is both ugly and a really bad habit.)
I agree with you that with some people, it doesn't provide anything special. I used to use matrix multiplication (use a long code) to calculate large fib number, therefore when I found this solution, I was very excited, so I wrote this post.
You can view my implementation as a suggestion for some people.
(I'm too lazy to write
long long)write ll instead of it
"long" is a keyword. "long" is highlighted by IDE, but "ll" is not.
# typedef long long ll;
cool. but can be cooler
answer in x. no map, time — logN.
Can we have a link to the full implementation of this programm?
oversolver can you explain , how is it work ?
f(n) = f(n)
f(n+1) = f(n) + f(n-1)
f(n+2) = f(n+1) + f(n) = f(n)*2 + f(n-1)
f(n+3) = f(n+2) + f(n+1) = f(n)*3 + f(n-1)*2
...
f(n+k) = f(n)*f(k+1) + f(n-1)*f(k)
f(2n+1) = f(n)*f(n+2) + f(n-1)*f(n+1)
so if we know f(n) and f(n-1) we can calculate f(2n) and f(2n+1)
"Let's divide n into groups by depth, you will realize a special property: Each depths only contains at most 4 values of n." some1 can explain why? I think on each depth contain 4^h values
*
I don't undertand different in two initialization:
F[0]=1; F[1]=1; cout<<f(n);
///////////////////// F[0]=1; F[1]=2; cout<<f(n-1);
It's giving me another answer.
F[0]=1; F[1]=1; cout<<f(n); ≠ F[0]=1; F[1]=2; cout<<f(n-1);
Is this better(efficient) than matrix exponentiation to calculate fibonacci??
please clarify me??
Similar in time complexity. Faster to code if you code matrix multiplication each time in a fibonacci question or slower if you use pre-written library for that. Hence, also faster/slower in performance depending upon your matrix multiplication code.
Key takeaway — If you write code from scratch each time and only have to code fibonacci use this else use pre-written matrix multiplication.
Thanks for your answer!!! in time complexity which is "best" or both have same time complexity?? for matrix multiplication => O(logn) for this code => O(log n*loglog n)
which is best i am confusing with log??
matrix multiplication has better asymptotically, but due to hidden constant factors this might run faster, can u see how crisp this code is..
How to do it when there is variation in Fibonacci series. For ex — F(n) = 2*F(n-1) + 3*F(n-2)
This code works for the case F[0]=1, F[1]=2:
If we choose different initial values, we need to make some modifications. The following code works for the case F[0]=200, F[1]=300:
This code is not giving correct answer.
for case F(n) = 2*F(n-1) + 3*F(n-2) answer should be 1 1 7 19 73..... but its giving 1 1 7 20 61.....
and where in the program you used coefficient 2 and 3
Please read my comment carefully, my first code is written for the case
F[0]=1, F[1]=2.Moreover, the output of my code is
1 2 7 20 61 ...instead of1 1 7 20 61 ...as you mentioned.If you want to code for the case
F[0]=F[1]=1, you can use my second code, just remember to setG[0]=1, G[1]=1.Thanks! But can you tell me that how to use coefficient of f(n-1) and f(n-2) in program. And where did you use those in your program.
Here you are:
return F[n] = (f(n1)*f(n2) + f(n1-1)*3*f(n2-1)) % M;return G[n] = (g(n1)*f(n2) + g(n1-1)*3*f(n2-1)) % M;F[1]=2;(at main())How can we prove the complexity of this algorithm?
i want to know how many time author spent in coma , because author of this post tell such stupid and wide known facts
This Formula has been posted in Geek for Geek, hasn't it?
Can someone explain why this code gets wrong answer if $$$ n=10^{19} $$$.
Try this nth Fibonacci problem
Did you use
unsigned long long?I’m not sure if people have said it already, but this is actually the same solution as matrix multiplication (only an optimization for the particular form of the recurrence matrix). More specifically, you may notice that matrices of form $$$F(a, b) = [[a, b], [b, a+b]]$$$ form a subring of matrices.
You can prove the above by arithmetic. In particular, identity is $$$F(1, 0)$$$, and Fibonacci matrix is $$$F(0, 1)$$$. This means that instead of storing the $$$2x2$$$ matrix, you could store just $$$a$$$ and $$$b$$$. This explains the formula and generalizes it.
Nice approach, We can also use Golden ratio stuff but it will give approx value, as we know that ratio of two consecutive fibonacci no. is nearly equal to golden-ratio.
Oh nice .. can you please tell any formula reagarding that so that we can calculate direct nth fibonaci no.?
Yes there is a formula also for the same Fn = [φ^n – (1-φ)^n]/√5
Here φ is Golden ratio whose value is approximately 1.618 and Fn is nth fibonacci no.