You are given N numbers in range 1 and 10^18. You should count the number pairs, which have at least one digit in common in their decimal notation and the position of the digits doesn't matter.
example input:
8 (N)
13 51 35 43
output:
5 (13,51),(51,35),(35,43),(51,35),(35,43)
The problem can be solved easily with a complexity of (2^10)*(2^10)(there are at most 10 different digits in a number). We have an array of size 2^10. We find the digits that a number contains for every number. Then we put the numbers, who contain the same set of digits in the same bucket. If a number contains digit 0 it is put in the bucket whose least significant bit is set, for digit 1, the buckets second least significant bit should be etc. After this, you can loop over the buckets like this:
for(int i=0;i<1<<N;i++)
for(int j=0;j<1<<N;j++)
if(i&j) //we should actually add a special case when i equals to j but anyway.
ans+=bucket[i]*bucket[j];
But my question is that could we do this in a better complexity?
I got an idea but I cant compute the bucket version it uses faster than 2^20. Here it is: If we could convert the array we computed above into this:
If a number contains digit 1, it should be put in every bucket whose bit for digit 1 is set. The same thing also applies to the other digits. Then we could compute the number of pairs with the inclusion&exclusion principle. We would just have a 2^N loop and if it has an odd number of set bits, we add it to the answer, if it doesnt, we subtract it from the answer. Actually I got an idea to compute the new array but it doesnt quite work. Some numbers get counted more than once. To fix it I have to use inclusion exclusion principle again. But then the complexity increases to 2^20 again. The wrong version follows:
for(int i=(1<<N)-1;i;i--)
for(int j=i;j;j&=j-1)
bucket[(j&-j)^i]+=bucket[i];
Could you please find a better way to solve this problem?
Thanks in advance.
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 166 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 160 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 17.11.2024 23:32:26 (j2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











You find for every digit how many numbers that contain this digit exist.
Then you compute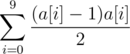
Why so? I'll leave the demonstration to you.
Your solution is incorrect. There can be two numbers containing for example digit 1 and 2 and with your formula, they will be counted more than once.
Well, if you want better solution... It looks like typical "very creative" problem — it is very common practice to ask about something opposite to real point of the problem:) Maybe people think that it increases difficulty, or originality, or beauty of problem, i don't know.
Instead of counting number of pairs with common digits — count number of pairs without common digits, and substract this number from total number of pairs.
How to solve problem about "no common digits"? First of all you can do bucketing like in your original solution. Then for every mask you can count numbers that contains only digits from this mask (but maybe not all of them) — counting sum over all submasks of all masks in 10*2^10 operations, moving bit by bit. And then for every bucket you should take inversion of it's mask and add to the answer result for this mask from previous step, multiplied by number of elements in given bucket. So if you have mask 1100011100 — you are interested in amount of numbers from bucket 0011100011 and all it's submasks, and you have calculated it on previous step.
BTW, with base10 even naive solution was good enough:)
I didnt quite understand how to count sum over all submasks of all masks but if we can do this, then we can calculate the bucketing that I failed to calculate in 10*2^N.
Just calculate the original bucketing array, but this time if ith bit is 0, then all numbers in this bucket contain ith digit. If ith bit is 1, then none of the numbers in this bucket contain ith digit.
After this just calculate the sum over all submasks of all masks in 10*2^10. Then when we want to know the numbers which are 0000110010(1 means this digit must be contained and 0 means it can be contained or not it doesnt matter) we just look at 1111001101. Is this right? And can you please further describe how to count sum over all submasks of all masks with 10*2^10 operations?
Sorry for not describing details about summation over submasks, i thought that this problem is well-known — it was used few times at CF rounds and also i've seen it in CF gym:) Here is the latest one — 449D - Jzzhu and Numbers, it has detailed tutorial, and you can also read someone's solution.
Thank you very much. The problem I asked and the one you have given have exactly the same solution :D.