Привет, расскажите, пожалуйста, задачи A, B, H.
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | jiangly | 3846 |
| 2 | tourist | 3799 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3590 |
| 6 | Ormlis | 3533 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3463 |
| 9 | ecnerwala | 3451 |
| 9 | Um_nik | 3451 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 165 |
| 2 | -is-this-fft- | 161 |
| 3 | Qingyu | 160 |
| 4 | atcoder_official | 156 |
| 4 | Dominater069 | 156 |
| 6 | adamant | 154 |
| 7 | djm03178 | 151 |
| 8 | luogu_official | 149 |
| 9 | Um_nik | 148 |
| 10 | awoo | 147 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2025 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 13.03.2025 12:27:18 (i1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











G тоже хотелось бы услышать.
A. Сжимаем координаты a[i], b[i], тк стрелять имеет смысл только в моменты времени b[i]. Также заметим, что стрелять имеет смысл только радиусами равными d[i].
Решаем кубической динамикой, состояние d[l][r] -- сколько стоит убить инопланетян с l<=a[i]<=b[i]<=r. Пересчет за линейное время — перебираем как выстрелить в самого большого d[i] среди них.
B:
Будем решать в онлайне, то есть, дописывать символ в конец и сразу выдавать ответ. Для этого будет поддерживать динамику DP[i] — минимальное количество ходов для получения i-го префикса. Тогда у нас есть два варианта развития событий:
То есть мы либо приписываем символ к уже построенной строке, либо сначала строим максимальный суффикс-палиндром чётной длины, а затем приписываем к нему слева оставшиеся символы. Легко видеть, что так мы учтём все варианты. Научимся получать cost[maxSufPal]. Утверждается, что мы всегда можем получить палиндром оптимально, если сначала построим его половинку, а затем удвоим её (для АС достаточно, если кто-то докажет, будет классно). Тогда cost[i] = minr[i] + 1, где minr — минимальная стоимость получения радиуса палиндрома i, то есть, его половинки. Здесь нам на помощь приходит дерево палиндромов (в данном решении используется только дерево для чётных длин). Для радиуса палиндрома i мы рассмотрим два случая, таких же, как и для всей строки:
parent[i] — предок вершины i в дереве палиндромов. maxSufPali — максимальный суффикс-палиндром радиуса палиндрома i. maxSufPali можно найти с помощью двоичного подъёма по дереву суффиксных ссылок. Итоговое решение: http://ideone.com/5uCXeB
Итоговая ассимптотика такого решения .
.
Можно переделать под O(n), если сначала построить дерево для строки, а затем поддерживать указатель на максимальный суффикс-палиндром радиуса, но тогда потеряем онлайновость.
Если вас смущают недоказанные утверждения (об оптимальности разбиения палиндрома) в решении, можно обойтись без них, рассмотрев три случая:
Последний случай покрывает все случаи "отрезания" символа с конца, кроме тех, когда был использован префикс-палиндром. Но в силу особенностей палиндромов, этот случай мы в любом случае рассматриваем в пункте 2 :)
После некоторого обсуждения с droptable было получено решение, которое является как чуть более простым в написании, так и более быстрым (работает за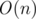 в онлайне). В нём мы каждый раз ищем максимальный суффикс-палиндром нового радиуса, начав поиски с расширения максимального суффикс-палиндрома старого радиуса. Такой подсчёт будет амортизированно линейным. И да, это не то же самое решение, которое он анонсировал ниже :)
в онлайне). В нём мы каждый раз ищем максимальный суффикс-палиндром нового радиуса, начав поиски с расширения максимального суффикс-палиндрома старого радиуса. Такой подсчёт будет амортизированно линейным. И да, это не то же самое решение, которое он анонсировал ниже :)
Код: http://ideone.com/9mZ8Aw
Кстати, а чем вам не нравится то, что описано в исходном комментарии? :)
Ok, Codeforces. Что вам не нравится? То, что я написал слишком очевидно? То, что я написал слишком скучно? То, что я написал слишком... сложно? Оо Или может вы просто не любите строки/дерево палиндромов/всё новое/...меня?
Anybody? Ну правда, как-то не круто, что комментарии по делу, а их только минусуют и никакого отклика. (Да-да, помню, "не пытайся познать логику голосов на кф", но всё же?)
Или может просто простым смертным нельзя разбирать задачи, которые на контесте не сдали ИТМО 1? :)
H. Решаем бинпоиском.
Заметим, что если есть какая-то подходящая последовательность действий, то в ней можно упорядочить всех по возрастанию v и она останется подходящей. Дальше проверяем достижимости динамикой за O(k*n). При выборе на k-ом шаге v[k][i] нам нужно знать оптимум по v[k-1][1..i-1], он считается чатсичными минимумами
Не понял. А зачем бин. поиск прикручивать, если динамикой можно и так ответ считать?
Я не умею без бинпоиска, тк тогда неясно какие состояния достижимы на k-м шаге.
Я не очень понял, что ты считаешь, но не правда ли то, что ты вначале из всех чисел вычитаешь C, а потом сравниваешь, что получилось больше либо равно 0?
Что-то типа того.
Как решать С и І?
I — отсортируем ребра по стоимости. Найдем для каждого ребра "току вхождения в остов" — левую границу в этом отсортированном массиве, такую, что если в запросе нижнее ограничение по стоимости выше, то наше ребро входит в остов, а если нет — то не входит, потому что выгодно взять что-то более дешевое. Теперь понятно, что когда приходит запрос [L,R] — нужно найти сумму стоимости всех ребер на отрезке [L,R], для которых "точка вхождения в остов" меньше L. Это можно сделать с помощью дерева отрезков — храним в каждой вершине отсортированные списки, по ним бинпоиск, частичные суммы прекалькулируем.
Как найти "точку вхождения"? Вспомним, как работает алгоритм поиска остова. Будем решать задачу, начиная с самых тяжелых ребер. Пускай у нас есть оптимальный остов на суффиксе массива, начиная с позиции i+1. Тогда при добавлении ребра i оно точно войдет в остов, а среди остальных ребер остова не более одного станет ненужным. Поэтому найдем точки вхождения за N*M — добавляя новое ребро, будем пересчитывать остов и удалять лишнее ребро, если такое есть. Для каждого ребра точкой вхождения в остов будет последняя итерация, на которой оно еще входило в наш промежуточный остов, т.е. первая итерация перед той, на которой мы его выбросим.
Можно и более straight-forward. Посчитаем для каждого ребра минимальный остов, если все более дешёвые рёбра удалить (считается за nm, т.к. при вычислении остова начиная с i-ого ребра достаточно рассмотреть только рёбра остова для i + 1-ого ребра). Запишем эти остовы в массив размера nm, и будем отвечать на запросы за бинпоиском.
бинпоиском.
Единственная проблема решения — нужно 400 метров памяти, но MLи в этот раз были щедрыми.
Можно ускорить препроцессинг до O(M log N), если искать самое тяжелое ребро на пути с помощью link-cut tree.
А на сами запросы можно отвечать с помощью персистентного дерева отрезков — после каждой итерации обновления остова добавим новое ребро в дерево отрезков на сумму, а старое — удалим, и сохраним копию дерева отрезков. Чтобы ответить на запрос, найдем бинарным поиском нужное дерево отрезков и сделаем в нем запрос на сумму на [L, R].
A — посчитаем за куб динамику "сколько нужно потратить, чтобы покрыть промежуток". Как это делать? Возьмем самый высокий отрезок, который полностью находится в нашем промежутке; понятно, что в него нужно походить, и делать это выгодно именно на его стоимость (высоту). Переберем, куда именно мы в него походим, этот ход разобьет нашу задачу на две подзадачи. При этом если какие-то отрезки проходили через точку нашего хода, то мы их точно покрыли (потому что походили на максимум), поэтому в полученных подзадачах инвариант сохраняется, и нас опять интересуют только отрезки, которые "полностью внутри".
G — Понятно, что последовательность сначала возрастает, потом убывает. При этом в возрастающей части нету одинаковых плиток, в убывающей — тоже. Закодируем одну сторону (например, возрастающую часть) маской из 0 и 1, которая говорит, какие степени в ней присутствуют. Зная номер хода и эту маску, мы можем восстановить и убывающую часть — нам известна сумма всего и сумма префикса, отсюда находим сумму суффикса, а по этой сумме сам суффикс можно восстановить жадно. Дальше осталось перебрать два возможных хода, проверить их на валидность и посчитать новые полученные маски.
H — бинарный поиск по ответу. Если у нас зафиксирован ответ, то нужно каждым ходом брать предмет, у которого "запас ценности" не ниже этого значения. Поэтому мы можем просто отнять от ценности предмета наше значение бинпоиска и перейти к известной задаче о дедлайнах: есть Х работ, для каждой известно время на ее выполнение и дедлайн выполнения; выполнить максимальное число работ. Эта задача решается сетом — сортируем работы по дедлайну, храним текущий сет-ответ, когда рассматриваем новую работу — она либо влазит (т.е. у нас достаточно времени на ее выполнение), и можно ее добавить в ответ, либо не влазит — тогда нужно сравнить ее с самой продолжительной работой из ответа, и поставить вместо нее, если это выгодно.
Как решать D?
Посчитаем динамику "сколько есть способов решить префикс длины X так, чтобы маска была Y". При этом маска — это 2 бита, один из которых говорит, что первая строка уже строго меньше второй, другой — что вторая строго меньше третьей.
Поделим все тройки символов на 9 классов, каждый из которых описывается 3ичной маской из 2 битов — первый символ больше/равен/меньше, чем второй; второй символ больше/равен/меньше, чем третий.
Троек символов всего несколько десятков тысяч, для каждой предпосчитаем, сколькими способами из нее можно получить тройку определенного класса, заменив ? на буквы.
Теперь можем считать саму динамику. Зная маску для префикса, переберем маску тройки, которую будем ставить — количество способов мы знаем, а маску-результат посчитать несложно (если первая строка была меньше за вторую, то она останется меньше; если были равны, то можем поставить либо равную пару символов, и строки останутся равны, либо же пару, в которой первый символ меньше — и первая строка тоже станет меньше).
Ответ на задачу — значение динамики для длины, равной длине самой длинной из строк, и маски, в которой первая строка меньше второй, а вторая меньше третьей.
Div.2 easier string problems N4 [C--] and O4 [Allo] using Perl as higher-level language (C--, Allo).
It seems that problemset from CERC 2014 was used today, but with renamed and shuffled problems.
Here you may find standings from original contest; i guess that mapping between problems is following:
Announcement at CERC site says that the contest data (problems, tests, and model solutions) will be posted at Sunday, November 23. — i guess Opencup was a reason for such a delay:) And we'll see solutions published soon.
How to solve E4 Exress As The Sum: faster than O(t * N ^ 3/4) ?, N = 10^9, t — unknown amount of tests. TL.
We can represent our segment as [x + 1, ..., x + k]. The sum equals to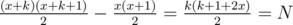 , so now it's clear that
, so now it's clear that 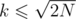 . Now we can iterate over all possible k.
. Now we can iterate over all possible k.
We can also show that the smallest k satisfying the equation is either a prime or a power of two. So it is sufficient to iterate over all primes and all powers of 2 less than or equal to The primes can be precomputed using Eratosthenes sieve. This gives total complexity of
The primes can be precomputed using Eratosthenes sieve. This gives total complexity of 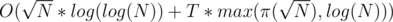
π(N) (the number of primes less than N) can be approximated as N / log(N).
The approximation gives total complexity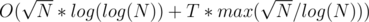 which is a little better than
which is a little better than  .
.
Actually my solution in received time limit exceeded and the optimization above helped to get it accepted. Maybe this is because I am using slow Ejudge server and it makes even the simplest problem more interesting:)
received time limit exceeded and the optimization above helped to get it accepted. Maybe this is because I am using slow Ejudge server and it makes even the simplest problem more interesting:)
Accepted code (a little ugly, I call 2^n a prime:): http://pastie.org/9739170
I haven't realized that we need no only primes, but primes**2 also. So I used all numbers from 2 to sqrt(N), but now I've written with primes, but still getting TL on tc 2. Can't understand why. (code). Ideone says, that such primes are generated in 0.1 sec (and there are 4.7k of them). And I can't understand what can be the biggest interval of numbers?
1) We do not need primes2, we need powers of two; i.e., 21, 22, 23, ..., . Your code gives incorrect result for 999990008. The answer should be
(24 = 16 elements)
2) I don't know Perl, but I couldn't get my Java solution working. 1 second time limit seems rather strict. Probably you should try C/C++.
.
Интересно, как решать O — Game (Div 2). Подскажите, если не составит труда, как должны действовать оптимально оба игрока в этой задаче?
.
Как решать J?
Требуемое отношение белых к черным фиксировано — оно совпадает с отношением общего числа белых к общему числу черных. Поэтому нужно просто жадно выделять блоки с заданным отношением. Это можно делать просто циклом.
У этого есть еще наглядная геометрическая интерпретация: представим, что мы изначально стоим в точке (0, 0), при встрече блока из w белых кирпичей мы идем на w вправо, а если мы видим блок из b черных кирпичей, то идем на b вверх. Получилась ломанная. Тогда нам необходимо взять прямую, содержащую начальную и конечную точки, а затем найти число целочисленных точек пересечения этой ломанной.
Задача B решаема и без дерева палиндромов.
Прогоним строку через Манакера. Далее запустим рекурсивную функцию, которая будет считать ответ на отрезке [L;R] следующим образом: и выбрать из них наименьший.
и выбрать из них наименьший.
Для текущей строки можно перебрать последнюю операцию по удвоению строки, то-есть все её чётные подпалиндромы. Однако заметим, что подпалиндромы, которые являются подотрезками других палиндромов, брать заведомо не выгодно. Остальные можно обработать следующим образом: для текущей строки переберём все подпалиндромы чётной длины и отсортируем их по начальной позиции и длине. Это делается за O(R-L), так как у нас уже есть посчитанный Манакер, а сортировку можно сделать подсчётом (для ОК достаточно было и обычной сортировки).
Теперь, перебирая последовательно отсортированные палиндромы, мы можем запоминать крайнюю правую границу и не брать те, которые являются подотрезками других, то есть те, у которых правая граница меньше чем чья-то предыдущая.
Осталось для каждого подпалиндрома (X;Y) посчитать ответ: кусочки по краям набираем по 1 символу, и половинку палиндрома считаем рекурсивно, то есть:
Что касаемо времени работы. Оценить его асимптотически я не смог. Для этого надо, как минимум, ответить на вопрос, который я задал здесь. Ну а на задаче с контеста мне удалось разогнать решение до времени меньше 1c (при ТЛ 30с), что вряд ли больше чем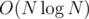
hello,where is the place to see and submitt the problem
hello,could some friend share the statements of the open cup gp of europe div2,thanks very much,my email is [email protected]