Azret's blog

How to find ALL prime numbers between N..N+M ?
By Azret, 10 years ago, translation, In English

Hello everyone!

So, the problem is to find all prime numbers on segment N .. N+M where 1010 <= N <= 1011 and 1 <= M <= 105.

My algorithm with O(M * sqrt(K)) asymptotic, where K — is the number that we are testing for primality exceeds TL.

  • Vote: I like it
  • +7
  • Vote: I do not like it

Comments Comments (6)
| Write comment?
»
10 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Have you tried segmented sieving method for the problem?

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

You can test if a number is prime with probabilistic methods as miller-rabin if i'm not wrong you can get O( it * log(n)^3 ) with it = number of iterations (with values near to 10^11 use 14) , in java is isProbablePrime with bigIntegers.

Code

Maybe this can get TLE if limit is strict as SPOJ , if this ocurrs you need to think in procesing primes <= sqrt( 10 ^ 11 ) .

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it +3 Vote: I do not like it
    1. You actually can use only four iterations with 100% correct result when N ≤ 1012 — see Wikipedia.
    2. Also you can multiply numbers with modulo less than 1012 using O(1) operations.
    long long multiply(long long a,long long b,long long m)
{
    long long a1=a>>20;
    long long a2=a&1048575;
    long long b1=b>>20;
    long long b2=b&1048575;
    return (a2*b2 + ((a1*b2+a2*b1)<<20) + ((a1*b1<<20)%m<<20))%m;
}

    And that means you only use per number.

    → Reply
»
10 years ago, # |
← Rev. 4   Vote: I like it 0 Vote: I do not like it

Why don't we just use a similar algorithm with Eratosthene sieve?

Firstly, generate all of primes between 1 and 106 (actually )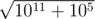

Second, create an array of bool, b[0..M]. b[i] = false if i+n hasn't been removed.

For each prime numbers in first step, try to clear all of its multipliers between N and N+M, then mark it onto array b.

This algorithm has the same complexity with Eratosthene sieve, isn't it?

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

You could use Eratosthene sieve,as some guys said. Also you can use Fermat law,which says that if p is prime then a^(p-1) MOD p = 1 1<a<p. The more a you take to test,the more sure it is that p is prime. Also to do the expontation you dont need to run it in O(N). You can use binary expontation right to left,which "break" the expontation into binary. For example if you have 5^5,because of 5=101(binary),the expontation will be 5^5=5^1+5^4.

here is wiki: http://en.wikipedia.org/wiki/Fermat_primality_test http://en.wikipedia.org/wiki/Modular_exponentiation

→ Reply