beatoriche's blog

Number of permutations with K or more fixed points
By beatoriche, 10 years ago, In English

The only way so solve it that I've found is to use https://en.wikipedia.org/wiki/Rencontres_numbers and calcuate 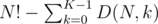, but I don't like that. Is there other way? Can we use inclusion-exclusion formula to calculate it?

  • Vote: I like it
  • -16
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it +13 Vote: I do not like it

Why don't you like that?

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can we use inclusion-exclusion formula to calculate it?

Yes we can. Notice that D(N, k) = C(N, k)·!(N - k), and derangement of (N - k) can be calculated this way

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

What does "fixed points" mean?

→ Reply
»
10 years ago, # |
  Vote: I like it +10 Vote: I do not like it

There is another solution involving dynamic programming and constructing permutations.

First, consider the following way of constructing all permutations of length n from all permutations of length (n - 1). Suppose we have a permutation of length (n - 1), for example, n = 6 and the permutation is a b c d e. Put the new element n at the back of the permutation. Then, swap the new last element with one of the elements, including itself. We get n different permutations:

a b c d e n   ->   n b c d e a   (swap elements 1 and 6)
a b c d e n   ->   a n c d e b   (swap elements 2 and 6)
a b c d e n   ->   a b n d e c   (swap elements 3 and 6)
a b c d e n   ->   a b c n e d   (swap elements 4 and 6)
a b c d e n   ->   a b c d n e   (swap elements 5 and 6)
a b c d e n   ->   a b c d e n   (swap elements 6 and 6, no change)

Note that different permutations a b c d e produce different permutations of length 6. So, this process allows to construct all permutations of length n from all permutations of length (n - 1).

Now, look what happens with the fixed points during this process. Let there be k fixed points in the permutation a b c d e. Clearly, 0 ≤ k ≤ (n - 1).

  • If we swap n with n, the number of fixed points increases by 1 (all the fixed points from a b c d e plus the new element n).

  • If we swap n with a fixed point (k possibilities), the number of fixed points decreases by 1.

  • If we swap n with an element which is already not in its place ((n - 1) - k possibilities), the number of fixed points stays constant.

We can now formulate a “forward” dynamic programming approach. If we know D(n - 1, k) = x, it contributes:

  • x to D(n, k + 1),

  • x·k to D(n, k - 1) and

  • x·((n - 1) - k) to D(n, k).

The “backward” dynamic programming solution (of the form D(n, k) = ...) can also be formulated.

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 3   Vote: I like it +10 Vote: I do not like it

    The problem of counting permutations with k fixed point is addressed in the book generatingfunctionology, as an example of the interpretation of the inclusion-exclusion principle in terms of generating functions.

    The approach yields the result that for a given n, if ak is the number of permutations of size n with exactly k fixed points, then its ordinary power series generating function is .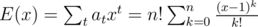

    This gives the formula

    , so we can compute the result in .

    → Reply