catlak_profesor_mfb's blog

Range Minimum Query(O(N),O(1))
By catlak_profesor_mfb, 10 years ago, In English

Enjoy! http://paste.ubuntu.com/9507070/ Tested in: http://codeforces.net/contest/494/submission/9121141

  • Vote: I like it
  • +38
  • Vote: I do not like it

»
10 years ago, # |
← Rev. 2   Vote: I like it +18 Vote: I do not like it

Now test to see how large the N has to be for it to be faster than segment trees ;p Though I have to admit, I didn't think it could be made so compact.

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    Well for N=100000 it is definetely faster :D To test it just overload the < operator and there you go. You can use it with everything as long as you overload < operator. The query returns the position of the minimum.

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    And I didnt try to optimize it. I just stopped coding when it worked

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think it is faster for N>15000 or something like that. I looked at 282-1-D(birthday) problems test cases

    → Reply
»
10 years ago, # |
  Vote: I like it +35 Vote: I do not like it 
ans=min(ans,lookup[sblock[t]&(~(((1<<(l-(r1*lg+lg)))-1)<<(r1*lg+(lg<<1)-l)))]+r1*lg+lg);

That looks really nice :)

→ Reply
»
10 years ago, # |
← Rev. 4   Vote: I like it 0 Vote: I do not like it

You split array into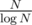 blocks of size 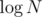, then build sparse table for each block and for all 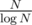blocks. Am I right?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yes you are right

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      But I dont actually build a sparse table like in regular rmq for the small blocks

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      then there are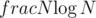 sparse tables, each of size 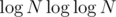. Therefore total complexity equals to .

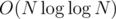      In order to build O(N) algorithm you have to go further and group blocks by its types, such that blocks with equal types will have equal sparse tables. It is exactly what Farach-Colton and Bender did

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        İt is not O(N) bits memory. İt is O(N) in a 32bit system.

        → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        As you can see I take 4 vectors, one of them holds the data which is O(N) and N/logN integers in another vector, N integers in another one and 2^(logN) integers which is N in another vector so total memory is O(N)

        → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        You are wrong with that part. The small blocks arent sparse tables. Please pay more attention to the code

        → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        If you are not satisfied please put a variable in every loop and increment it. And test it with different N. You will see a linear increase.

        → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

double post

→ Reply
»
10 years ago, # |
  Vote: I like it -9 Vote: I do not like it

"block" is a sparse table for log(n) blocks of "data". Right? What do "sblock" and "lookup" exactly do?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    sblock is small blocks of size logn and it helps us extract the min in constant time from blocks of size logn

    → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Nice One! But not efficient for large value of N.

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Read the topic here e-maxx.ru/algo

→ Reply