Range Minimum Query(O(N),O(1))

→ Обратите внимание

До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
37:25:21
Зарегистрироваться »

*есть доп. регистрация

→ Лидеры (рейтинг)

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

Страны | Города | Организации

Всё →

→ Лидеры (вклад)

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Всё →

→ Найти пользователя

→ Прямой эфир

Детальнее →

Блог пользователя catlak_profesor_mfb

Range Minimum Query(O(N),O(1))

Автор catlak_profesor_mfb, 10 лет назад, По-английски

Enjoy! http://paste.ubuntu.com/9507070/ Tested in: http://codeforces.net/contest/494/submission/9121141

advanced data structure

catlak_profesor_mfb
10 лет назад
21

Комментарии (21)

Написать комментарий?

Rivx

10 лет назад, # |

← Rev. 2 →

+18

Now test to see how large the N has to be for it to be faster than segment trees ;p Though I have to admit, I didn't think it could be made so compact.

→ Ответить

catlak_profesor_mfb

10 лет назад, # ^ |

← Rev. 3 →

Well for N=100000 it is definetely faster :D To test it just overload the < operator and there you go. You can use it with everything as long as you overload < operator. The query returns the position of the minimum.

→ Ответить

catlak_profesor_mfb

10 лет назад, # ^ |

And I didnt try to optimize it. I just stopped coding when it worked

→ Ответить

catlak_profesor_mfb

10 лет назад, # ^ |

I think it is faster for N>15000 or something like that. I looked at 282-1-D(birthday) problems test cases

→ Ответить

proVIDec

10 лет назад, # |

+35

ans=min(ans,lookup[sblock[t]&(~(((1<<(l-(r1*lg+lg)))-1)<<(r1*lg+(lg<<1)-l)))]+r1*lg+lg);

That looks really nice :)

→ Ответить

catlak_profesor_mfb

10 лет назад, # ^ |

← Rev. 3 →

I know

→ Ответить

CountZero

10 лет назад, # |

← Rev. 4 →

You split array into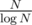 $\text{[math]}$ blocks of size 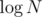$\text{[math]}$ , then build sparse table for each block and for all 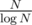$\text{[math]}$ blocks. Am I right?

→ Ответить

catlak_profesor_mfb

10 лет назад, # ^ |

Yes you are right

→ Ответить

catlak_profesor_mfb

10 лет назад, # ^ |

But I dont actually build a sparse table like in regular rmq for the small blocks

→ Ответить

CountZero

10 лет назад, # ^ |

then there are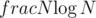 $\text{[math]}$ sparse tables, each of size 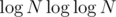$\text{[math]}$ . Therefore total complexity equals to $\text{[math]}$ .

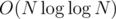In order to build O(N) algorithm you have to go further and group blocks by its types, such that blocks with equal types will have equal sparse tables. It is exactly what Farach-Colton and Bender did

→ Ответить

catlak_profesor_mfb

10 лет назад, # ^ |

İt is not O(N) bits memory. İt is O(N) in a 32bit system.

→ Ответить

catlak_profesor_mfb

10 лет назад, # ^ |

As you can see I take 4 vectors, one of them holds the data which is O(N) and N/logN integers in another vector, N integers in another one and 2^(logN) integers which is N in another vector so total memory is O(N)

→ Ответить