Hi, everybody.

I'm interested in how to solve the next problem 18.

It's obvious, that if 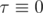curve is plane.

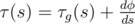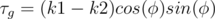Transform torsion at point ρ(s) as , where — is geodesic torsion at the point, and φ is angle between osculating plane and tangent plane. , where k1 and k2 are principal curvatures.

Also, if we consider the case, when curve doesn't lay in plane, and surface is a sphere. At any point on sphere k1(s) = k2(s), and we have to prove that .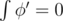

In other cases we are able to find a point, where k1 ≠ k2. And I guess we should constract such curve in a neighbourhood of that point .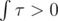

Any ideas how to complete this solution? Or any others solutions are welcome.

UPD1 Solution for sphere.

Let 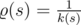. If the curve lays on the sphere then the equality 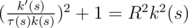holds. By means of a little transformation of this equality, we can obtain 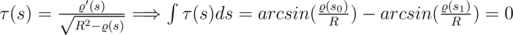. 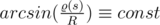, because the radius of curvature is constannt in any point on the sphere.