В этой задаче требовалось сделать то, что написано в условии. Считать числа и определить у кого из ребят больше баллов.
Асимптотика: O(1).
Для начала немного переформулируем задачу. Был дан ориентированный граф, вершинами которого являются хэндлы пользователей, а ребрами запросы изменения хэндлов. Он состоит из некоторого количества цепочек, нужно было найти их количество, начальные и конечные вершины каждой цепочки. То есть у каждой вершины входящая и исходящая степень не превосходит 1. Ввиду последнего ограничения, ребра этого графа можно хранить в словаре(в C++ — std::map\unoredered_map, Java — TreeMap\HashMap), где ключом является вершина из которой исходит ребро, а значением — вершина, в которую оно входит.
Каждому уникальному пользователю соответствует вершина с нулевой входящей степенью. Из всех таких вершин нужно переходить по ребру, до тех пор, пока существует переход. Чтобы найти вершины с нулевой степенью, запомним вершины в которые входит ребро, и добавим их в множество(в C++ — std::set\unoredered_set, Java — TreeSet\HashSet).
Асимптотика: 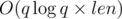 .
.
Заметим, что у непустого леса найдется вершина со степенью 1(такая вершина называется листом). Будем удалять ребра графа по очереди и поддерживать актуальные значения (degreev, sv), до тех пор пока он не станет пустым. Для этого будем поддерживать очередь(или стек) вершин являющихся листьями. На очередной итерации мы достаем вершину v из очереди, и удаляем ребро (v, sv), для этого делаем degreesv -= 1 и ssv ^= v. Если у вершины sv степень стала равной 1, то добавим ее в очередь.
Необходимо обработать случай, когда мы достаем вершину v из очереди и у нее degreev = 0, тогда стоит проигнорировать это, так как мы уже удалили нужное ребро.
Асимптотика: O(n)
504B - Миша и сложение перестановок
Для решения данной задачи необходимо научиться находить порядковый номер данной перестановки и перестановку по данному порядковому номеру. Так порядковые номера имеют достаточно большую длину, будем хранить их в факториальной системе счисления. То есть число x будем представлять как 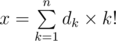 .
.
Чтобы найти порядковый номер перестановки, заменим каждое число в перестановке на количество чисел стоящих правее и меньше его. Таким образом мы получим число, записанное в факториальной системе счисления.
Чтобы получить по порядковому номеру перестановку необходимо провести обратную процедуру, для этого потребуется находить k-тое по величине число в множестве, и добавлять элемент в множество. В обоих случаях нам пригодится дерево отрезков, которое позволяет отвечать на запросы такого вида.
В итоге получаем, что нам необходимо получить индексы перестановок, сложить их в факториальной системе счисления по модулю n!, и провести обратное преобразование. Для лучшего понимания ознакомьтесь с wiki и/или любым прошедшим решением.
Асимптотика:  или
или 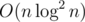 .
.
Заметим, что если количество элементов, встречающихся нечетное число раз, больше одного — ответ равен нулю. Аналогично, если массив изначально является палиндромом — ответ 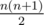 .
.
Будем обрезать с обоих концов палиндрома одинаковые символы, пока это возможно. Пусть при этом мы получили массив b длины m, его первый и последний элементы различны. Нужные нам отрезки [l, r] содержат какой-то префикс или суффикс массива b.
Найдем минимальные длины суффикса и префикса. Здесь нужно рассмотреть два случая: переходит ли кратчайший префикс/суффикс за середину массива или нет. Определить минимальные длины можно с помощью бинпоиска или проходом по массиву и поддержанием количества каждого элемента слева и справа от текущего индекса. Обозначим минимальные длины префикса за pref, и суффикса за suf. Тогда ответ 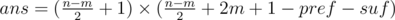 .
.
Асимптотика O(n) или  .
.
Переведем каждое число в двоичную систему счисления, для одного числа это делается MAXBITS2 c малой константой, если хранить число в системе счисления с основанием 109 или 1018. MAXBITS ≤ 2000.
Для решения задачи нам потребуется небольшая модификация алгоритма Гаусса. Будем обрабатывать запросы по одному, проделывать итерацию алгоритма Гаусса, и поддерживать следующую информацию, для бита с индексом i хранить индекс p[i] запроса, или - 1, если такого запроса нет, у которого этот бит является младшим выставленным после его(запроса) нормировки. Нормировкой я называю, процесс, в котором число приводится к такому виду, что его индекс наименьшего выставленного бита максимален. При нормировке мы можем XOR-ить число с любыми другими числами из запросов с индексами меньше текущего. Также нам понадобится информация о том, с числами из каких запросов мы проXOR-или текущее число чтобы его отнормировать, будем хранить это в битсете x[j], где j-индекс запроса.
Итак, обрабатывая очередной запрос v, мы пробегаем по его битам от младшего к старшему. В случае если текущий бит i выставлен, мы пытаемся обнулить его. Если p[i] = - 1, то обнулить этот бит нельзя и мы заканчиваем обработку этого запроса, иначе XOR-им текущее число с отнормированным числом из запроса p[i], а так же XOR-им x[v] с x[p[i]]. Если после обработки запросов нам удалось обнулить число, тогда ответ на запрос — да, и в битсете x[v] содержится множество индексов являющееся ответом, иначе — нет.
Асимптотика решения O(m × MAXBITS × (MAXBITS + m)) с малой константой, засчет битового сжатия.
Построим heavy - light декомпозицию дерева и запишем все строки соответствующие heavy-путям идущим вверх и вниз в одну строку T.
Обрабатывая очередной запрос разобьем пути (a, b) и (c, d) на части, целиком принадлежащие heavy-путям. Таких частей будет  . Заметим, что каждой части пути соответствует некоторая подстрока T.
. Заметим, что каждой части пути соответствует некоторая подстрока T.
Теперь для ответа на запрос нам необходимо находить наибольший общий префикс двух подстрок в строке. Это можно сделать, найдя суффиксный массив строки T, массив lcp и построить sparsetable на минимумы на нем.
Асимтотика: 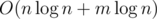
Для лучшего понимания ознакомьтесь с моим решением.
P.S. Вместо суффиксного массива можно использовать хэши, сохраняя асимптотику.
P.P.S. Решения, использующие двоичный подъем и хэши, отсекались по времени большими тестами.










При переходе по ссылке на решение задачи Е див.1 пишет, что недостаточно прав для просмотра.
Неправда
For problem 504B (501D for Div 2) we can also use square root decomposition instead of trees in order to transform the permutation, and still wouldn't hit the given time limit.
В задаче D Div1 о каком алгоритме Гаусса идет речь?
Решения систем линейный уравнений
Я изначально так и подумал, но по решению так и не понял каким боком тут алгоритм Гаусса — нужно все таки разобраться с решением. Плюс сбило с толку, что в описании решения речь идет о итерациях алгоритма, а Гаусс все-таки прямой метод решения СЛАУ, а не итерационный.
У Гаусса довольно много применений. Например, смотрим здесь.
Задача D довольно известная, и речь идет о том, чтобы с помощью Гаусса поддерживать базис пространства векторов; когда добавляем новый вектор — делаем фактически то же самое, что и при переходе к очередному уравнению в случае решения СЛАУ. У нас два варианта — либо вектор линейно независим, тогда представить его в виде xor'а других векторов не получится, и у нас увеличилась размерность пространства, либо же он линейно зависим — тогда мы найдем его представление в виде комбинации предыдущих векторов и выведем его.
Огромное спасибо. Эта идея открыла мне глаза на решение задачи =) P.S. Я сам довольно плотно занимаюсь факторизацией матриц разной структуры методами Гаусса, Холецкого и т.д. Чуть задело, что не мог понять как тут применяется мой "профильный" метод =)
Problem C can also be done without observing that every good interval is an "overinterval" of those 2 ones. For each starting l I just computed smallest good r using sliding window idea and maintaining some informations about actual interval. Those informations consisted of number of bad pairs (i, n - i + 1) completely outside of interval (this needs to be equal to 0) and some counters of needed values to make sure that pairs of form (i, n - i + 1) where only one of those two indices belongs to our interval can be satisfied. See my submission: 9413910
If I'm not mistaken problem E can be done if we will store jumppointers together with hashes of strings represented by paths they are corresponding to (in both directions from down to up and from up to down) and that should be easier to code.
Do you really think that if your solutions looks like those: https://ideone.com/42hc8F and http://ideone.com/2OxibB then this problem (E) is appropriate as one of 5 problems given in a 2-hour long contest?? You seem to forgot that you had unbounded time and contestants got <=1 hour for that problem alone. Moreover you purposefully set constraints so that solutions in slightly slower complexities will get TLE. Telling by number of lines of your solutions that was another "great" idea.
There is a "P.P.S" in russian version of E editorial, that says that there were big tests against jumppointers + hashes. At least if I understand what you mean here. However, some contestants got AC with this idea tweaked a bit (which resulted in many-many cases in their code).
I think the prolem can be made using O(1) time for query.My idea is maintaining something like a suffix array on tree.You just sort all the suffixes(like node i and his 2^j th ancestor(which you build like a RMQ)) and you are going to keep sa second suffix array with these string reversed, and for these, you preacalculate lcp between two consecutive suffix, than lcp being tha minimum between the LCP between poitions in sorted array of the two suffixes.You also noeed to get LCA in O(1) with an easy euler crossing and maintaining anther rmq.And, yeah, the sources are two big and the official idea is to easy and to hard to code for a div1E problem, which should be very interesting and the code should be about 150 rows, in worst case, or something like that.
I'm curious about that solution, most people tried doing it in O(log^2 N) per query but it is too slow. If we try to do it in O(log N) going up is not the problem but going down is. I managed to do something like that 9420369 but it was ugly and long too, and constant factor was very large, I had to do about 10 O(log N) operations for a single query. Is there anything better?
For 501B we could use two lists(python3) for solving rather than using dictionaries. 9409569
Your solution has complexity O(q2 × len). I described significantly faster one.
Подскажите, как можно решить B div1 за O(n logn)? (знаю, что за O(n log^2n) можно с помощью бинпоиска и дерева отрезков)
Наверное, просто деревом отрезков, а не фенвиком и бинпоиском.
Can someone please explain problem 504C — Misha and Palindrome Degree in detail? help is appreciated :).
Ложь и провокация, у меня на дорешивании прошло: 9456035 ;)
Правда, мне пришлось для этого избавиться от
O(log²)на запрос, объединив бинпоиск и двоичный подъём в один общий логарифм. Видимо, это то самое «this idea tweaked a bit (which resulted in many-many cases in their code)», о котором писал ItsLastDay в комментариях выше.Я имел ввиду решение за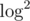 на запрос, в пример самому банальному :)
на запрос, в пример самому банальному :)
Hello can someone explain that how to add the two permutations in Factorial number system.
Thank you.
I wrote a blog for 501 D Misha and permutations. Here it is.
You can find the details there.
FigureOutByYourself-forces.
HELP, Can anyone explain the addition of two numbers in the factorial number system without converting them to decimal under n! as required in Misha and Permutations Summation
Imagine you have the factoradic F = (2, 3, 0, 1, 0) with n = 5, which means 2*4!+3*3!+0*2!+1*1!+0*0!
Now lets calculate F+F = (2+2, 3+3, 0+0, 1+1, 0+0) = (4, 6, 0, 2, 0), which means 4*4!+6*3!+0*2!+2*1!+0*0!. In the Factorial Number System, it makes no sense to use a number greater than the factorial used in the same position, as it could be represented as the next position (e.g 5*3! = 1*4!+1*3!). So we should modified our previous calculation F+F to be represented in this way F+F = (2+2, 3+3, 0+0, 1+1, 0+0) = (4, 6, 0, 2, 0) = (1, 0, 2, 1, 0, 0) = 1*5!+0*4!+2*3!+1*2!+1*1!+0*0!
And when you need to calculate F*F mod n! (as n = 5), it is the same as removing the first element of the result.
Here is my solution, with a class Factoradic which might help you :)