В этой задаче нужно было сделать то, что написано в условии: построить таблицу(двумерный массив) по указанным правилам и найти максимум в таблице.
Можно было заметить также, что максимальный элемент находится в правом нижнем углу.
Также проходило и просто решение рекурсией:
def elem(row, col):
if row == 1 or col == 1:
return 1
return elem(row - 1, col) + elem(row, col - 1)
Кроме того, можно было заметить в таблице Треугольник Паскаля и понять, что ответ — это 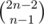
Готовил: riadwaw
Разбор от: riadwaw
Пусть найдутся две кучки, в которых количество камней отличается строго больше чем на k, тогда решения не существует:
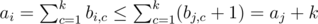
Пусть теперь M = max ai ≤ min ai + k = m + k, покажем, как построить правильную раскраску:
- покрасим по m камней в каждой кучке в первый цвет
- в каждой кучке все оставшиеся камни покрасим в любые различные цвета(можно использовать первый еще один раз) (это можно сделать т.к осталось не более k камней.
Заметим, что 1-ый цвет встречается в каждой кучке m или m + 1 раз, а остальные цвета — 0 или 1 раз
Готовил: Kostroma
Разбор от: riadwaw
Будем действовать жадно. На первом шаге найдём минимальное число b1 с суммой цифр a1. Далее, на i-м шаге найдём минимальное число bi с суммой цифр ai, которое больше чем bi - 1.
Почему это правильно? Поскольку b1 — минимальное число с суммой цифрой a1, то первое число не меньше чем b1. Далее по индукции: i-е число не меньше bi, поэтому (i + 1)-е число должно иметь сумму цифр ai + 1 и быть больше чем bi. Но минимальное такое число как раз bi + 1. Значит, построенный пример даёт оптимальное решение задачи.
Осталось научиться решать подзадачу: найти минимальное число с суммой цифр x, которое больше y. Она решается стандартным подходом: идем по цифрам числа y с младших разрядов и пытаемся увеличить соответствующую цифру (считаем, что каждое число содержит бесконечно много нулей слева от своей старшей цифры). Пусть справа осталось k цифр, тогда сумма этих k цифр может быть любым натуральным числом от 0 до 9k. Если получилось увеличить текущую цифру так, что при каком-то выборе цифр справа от неё получилась сумма x, то мы получили ответ. Заметим, что цифры справа от текущей позиции в таком случае нужно заполнять жадно с младших разрядов, каждый раз используя максимально возможную цифру — таким образом мы действительно получим минимальный ответ.
Оценим максимальную длину ответа, т.е. числа bn. Заметим, что если длина десятичной записи bi хотя бы 40, то в промежутке между 10k и 10k + 1, где k — наименьшее натуральное число, такое что 10k ≥ bi, есть числа со всеми суммами цифр от 1 до 9k. Так как все ai ≤ 300, то при 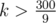 в отрезке [10k, 10k + 1] есть любая из интересующих нас сумм цифр. Значит, при достижении 40-значного числа на каждом шаге количество цифр в десятичной записи bi увеличивается не более чем на 2, а значит итоговый ответ будет иметь десятичную записать не длиннее 640 цифр (еще немного подумав, можно понять, что эту оценку можно усилить до 340).
в отрезке [10k, 10k + 1] есть любая из интересующих нас сумм цифр. Значит, при достижении 40-значного числа на каждом шаге количество цифр в десятичной записи bi увеличивается не более чем на 2, а значит итоговый ответ будет иметь десятичную записать не длиннее 640 цифр (еще немного подумав, можно понять, что эту оценку можно усилить до 340).
Значит, получаем решение за O(n·maxLen), где maxLen — максимальная длина ответа. Поскольку n ≤ 300, maxLen ≤ 640, такое решение с запасом проходит.
Готовил: Endagorion
Разбор от: Kostroma
Заметим, что если в корректном ответе ко всем bi добавить 1, а из всех ai вычесть 1 (и при необходимости добавив k), то ответ останется корректным. поэтому можно считать, что ai = 0, тогда из первой строки однозначно восстанавливаются bj, а по ним — ai (Можно пока разрешить им быть отрицательными, а потом добавить нужное число раз k). Теперь для любых i, j мы можем найти "ошибку" 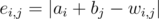 .
.
Если все ошибки нулевые — всё отлично, возьмем k достаточно большим и ответ будет автоматически корректным.
Для того, чтобы не нарушалось условие в клетке (i, j) необходимо и достаточно, чтобы ei, j делилось на k. Таким образом, k должно быть делителем gcdi, j(ei, j). При этом, k должно быть строго больше, чем все числа в таблице. Таким образом выгодно попытаться поставить k = gcdi, j(ei, j), что можно сделать, если k > maxi, j(wi, j). В противном случае ответа не существует.
Готовили: Kostroma, riadwaw
Разбор от: riadwaw
Посчитаем суммы vowel(si) на всех префиксах строки, чтобы за O(1) можно было легко посчитать сумму vowel(si) на любой подстроке.
Будем перебирать m с 1 до 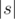 . При фиксированном m найдем сумму простых мелодичностей всех подстрок длины m. Для этого посмотрим, сколько раз i-й символ s входит в эту сумму.
. При фиксированном m найдем сумму простых мелодичностей всех подстрок длины m. Для этого посмотрим, сколько раз i-й символ s входит в эту сумму.
При m = 1 каждый символ входит ровно один раз. При m = 2 все символы, кроме крайних — 2 раза, крайние 1 раз. При m = 3 все 3 раза, кроме второго и предпоследнего(2 раза) и первого и последнего (1 раз).
При m = |s| каждый символ входит один раз, как и в случае m = 1, а при m = |s| - 1— 2 раза кроме крайних, как и в случае m = 2.
В общем случае, i-й символ входит min(m, |s| - m + 1, i, |s| — i + 1) раз. Можно заметить, что при переходе от m к m + 1 к сумме прибавляются вхождения символов на подотрезке с m по |s| - m + 1(если m > |s| - m + 1, то убавляются на подотрезке с |s| - m + 1 по m).
Таким образом, можно легко пересчитать сумму вхождений гласных при переходе от m к m + 1, прибавив(убавив) сумму vowel на подстроке. Итоговое решение за O(N).
Готовил: zemen
Разбор от: zemen
Рассмотрим произвольное дерево на n вершинах. Подвесим дерево за вершину 1, и пусть массив a — результат работы dfs-а. Тогда вершины поддерева с вершиной v, 1 ≤ v ≤ n, записаны в подмассив a[lv..lv + sizev - 1], где lv есть позиция вершины v в массиве, а sizev — размер поддерева.
Решим задачу, используя сей факт и ДП на подотрезках. Пусть задан массив a, и пусть e[l, r] есть количество деревьев, составленных из вершин a[l], a[l + 1], ..., a[r], т.ч. dfs, запущенный из вершины a[l], выведет вершины в том же порядке, в котором они представлены в массиве a. Тогда, если l = r, то e[l, r] = 1; иначе 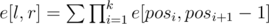 , где сумма берется по всем возможным множествам детей a[l], т.е. по всем таким k;pos1, ..., posk + 1, что l + 1 = pos1 < pos2 < ... < posk + 1 = r + 1, 1 ≤ k ≤ r - l, a[pos1] < a[pos2] < ... < a[posk] (вспомним, что в dfs-е дети перебираются в порядке возрастания). Однако даже при наличии ответов для подотрезков отрезка [1..n] решение с использованием такой формулы будет работать экспоненциально долго.
, где сумма берется по всем возможным множествам детей a[l], т.е. по всем таким k;pos1, ..., posk + 1, что l + 1 = pos1 < pos2 < ... < posk + 1 = r + 1, 1 ≤ k ≤ r - l, a[pos1] < a[pos2] < ... < a[posk] (вспомним, что в dfs-е дети перебираются в порядке возрастания). Однако даже при наличии ответов для подотрезков отрезка [1..n] решение с использованием такой формулы будет работать экспоненциально долго.
Финальная идея заключается во введении d[l, r]: = e[l - 1, r], 2 ≤ l ≤ r ≤ n. Действительно, из вышеприведенной формулы следует, что d[l, r] = 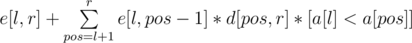 ([утверждение] определим как 1, если утверждение истинно, и 0, если ложно), а также e[l, r] = d[l + 1, r]. Таким образом, d[l, r] и e[l, r] для каждого отрезка вычисляются за линейное время; ответом же на задачу является e[1, n]. Итоговая асимптотика решения O(n3).
([утверждение] определим как 1, если утверждение истинно, и 0, если ложно), а также e[l, r] = d[l + 1, r]. Таким образом, d[l, r] и e[l, r] для каждого отрезка вычисляются за линейное время; ответом же на задачу является e[1, n]. Итоговая асимптотика решения O(n3).
Готовил: DPR-pavlin
Разбор от: DPR-pavlin











круто, за 16 часов до контеста разбор) это получается он скрытым был, или просто никто не смотрел?
А когда по остальным задачам?
Он был в черновиках. Время показывается на момент создания.
E добавил.
спасибо. можете подсказать, почему в моем решении такая большая погрешность получается?
9657673
Могу посоветовать разобраться начинать с теста "A". У вас выводит 2, хотя ясно, что подстрока всего одна.
случай с длиной строки, равной 1 я не рассмотрел конечно, но это мое решение, которое я даже не послал во время контеста. Получается слишком большая погрешность, и я не понимаю, почему. :(
насчет этого вы могли бы мне обьяснить?
Ну тут дело не в длине 1, для строки АА тоже выводит 5 вместо 3. Я не читал ваш код, но может быть вы забыли где-нибудь +/-1 ?
зафиксил такие случаи. меня интересует, опять же, почему погрешность большая 9657853
пардон, не зафиксил.
извините, решение бредовое, нашел ошибку)
Спасибо
Добрался до компа, сейчас станет чуть лучше.
Модуль исправил, спасибо.
Не везде.
Спасибо еще раз, теперь кажется пофиксил
Problem E can also be solved using DP as follows — The required answer is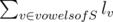 where
where 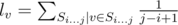 . Define dp[i] to represent ls[i]. Then, dp[i+1] = dp[i] + h[n-i-1] — h[i+1], dp[0] = h[s.size()] where h[i] is the ith harmonic number. Link to my solution.
. Define dp[i] to represent ls[i]. Then, dp[i+1] = dp[i] + h[n-i-1] — h[i+1], dp[0] = h[s.size()] where h[i] is the ith harmonic number. Link to my solution.
Super fast tutorial. Hope it will be finished soon and also problem D and E will be translated.
Задача F:
Тогда, если l ≤ r, то e[l, r] = 1Почему так?
Да и каким образом может быть l > r, если есть последовательность a[l],a[l+1], ... , a[r]?
Прошу прощения, конечно же имелось ввиду l = r )))
спасибо, туплю что-то, мог бы и сам додуматься)
И еще мне кажется, что тут опечатка:
d[l, r]: = e[l - 1, n].Должно вроде как быть d[l, r]: = e[l - 1, r].
Альтернативный взгляд на E:
Рассмотрим одну конкретную позицию i, на которой стоит гласная, и её вклад в общую сумму. Введём число k = min(i + 1, n - i) (позиции 0-индексированные). Теперь рассмотрим различные длины (пусть длина равна m):
Введём два вспомогательных массива, чтобы с их помощью быстро пересчитывать ответ.
Собирая всё воедино: вклад символа i равен k(1 + s1[n - k + 1] - s1[k]) + s2[n - k + 2].
Решение: 9658642
Мне также показалось, что авторское решение F слишком формальное, попробую описать своё. Пусть DP[l][r] — количество различных корректных лесов, описываемых подотрезком [l, r]. Будем считать лес корректным, если номера корней в нём образуют возрастающую последовательность, а также каждое дерево при удалении корня превращается в корректный лес. Легко видеть, что при таком описании ответ содержится в DP[1][n - 1] (снова 0-индексация). Теперь научимся пересчитывать ответ. Это делается достаточно известным комбинаторным приёмом — рассмотрим первый элемент множества и всю оставшуюся его часть раздельно. В данном случае это будет означать, что мы выделим первое дерево в лесу и добавим к ответу произведение числа способов задать ему поддерево на число способов корректно описать оставшуюся часть леса. Пусть мы рассматриваем отрезок [i, i + j]. Будем считать, что первое дерево описано на подотрезке [i, i + k - 1] (т.е., его лес описан подотрезком [i + 1, i + k - 1], а все оставшиеся на [i + k, i + j]. Тогда если a[i] < a[i + k], сделаем DP[i][i + j] + = DP[i + 1][i + k - 1] * DP[i + k][i + j], иначе — проигнорируем подотрезок.
Решение: 9658715
Problem E: "If m > |s| - m + 1, then SP is decreased by the number of vowel occurrences in the substring from |s| - m + 1 to m." Shouldn't it be "from |s| - m + 1 to m — 1"? Consider the first example, IEAIAIO. For m = 4 the numbers of times characters are included form this sequence: 1, 2, 3, 4, 3, 2, 1. For m = 5 the sequence is as follows: 1, 2, 3, 3, 3, 2, 1. So SP decreased only by vowel from position 4, i.e. by vowels from |s| — m + 1 to m — 1. Second A is still included in 3 substrings.
PS "the numbers of times characters are included form this sequence" — did I write it correctly? If not, how should I write it in English? :)
You're correct. The proper indices should be from |s| - m - 1 to m when decreasing and from m to |s| - m - 1 when increasing (assuming the indices are 0-based).
Actually "increasing" indices are correct, I think :)
Example: IEAIAIO.
For m = 1 you have: 1, 1, 1, 1, 1, 1, 1.
And for m = 2: 1, 2, 2, 2, 2, 2, 1. So position |s| — m + 1 = 7 — 2 + 1 = 6 is also increased.
Proof by example, my favourite type of "proof" ;)
Edited 2: All right, I was thinking in different index bases, that explains it all. Okay so here's the deal: In the editorial we're moving from m to m + 1 and using the old m to calculcate the indices, while you're using m + 1. The editorial still needs correction, but you get the idea :)
For problem D:
Let M be the maximum number in W
If K > 2 * M, the modulus will change by some constant. So we can assume that: 2 * M >= K > M.
Of course the trial and error approach wouldn't pass. We can first assume that k = M + 1 (or any other value larger than this). If this caused any error we can then change K only one time to (2 * M minus current element that caused the error in W). If it caused another error then the answer must be "NO".
I set maxLen 300 in Problem C... I accepted after I changed it to 340
In the tutorial of C Problem. The last two paragraph, 'than' equals to 'then'?... Why not maxlength is 34, cause 34 * 9 = 306 > 300?
Consider the following data: 300 300 1 1 ... 1 The length is 333.
Вы пишете разбор по задаче С: "Осталось научиться решать подзадачу: найти минимальное число с суммой цифр x, которое больше y. Она решается стандартным подходом:" А можно подробнее узнать как получить число больше заданного Y с суммой цифр X. Спасибо.
После этих слов подход как раз и объясняется.
Как раз после этих слов все объяснено общими словами. А можно где нибудь увидеть как это делается на практике, если это считается стандартной задачей.
Ну вроде бы все также просто, как и написано.
Одно из авторских решений: http://ideone.com/nfkE5n
А вообще можно просто открыть решения кого-то из решивших
Can someone write more detailed idea or pseudo-code of problem C solution, when you need to find next least number with same sum of digits?
Look at each suffix of previous number, from left to right. If suffix begins with diggit c and has n digits, then c+1<=sum<=9n We are checking this condition, while its right. Let's pretend its false for suffix with N digits. Then we are changing digit on (N+1)-th place from c+1 to 9, trying to get number with fixed sum. If we can't do this, then we changing (N+2)-th digit, and go on and on, while we don't get required number
Example: If we have number 391, and number with sum 10 to find, then suffix 391, sum is 10: we can get sum from 4 to 27. Go to next suffix
suffix 91, sum is 7: we can get sum from 10 to 18 (yes, we cannot get sum 10, but this is not important). Condition is false. Go to previous suffix to increase third digit
4??, sum is 6, we can do this with number 406.
This algorithm can be realise with recurtion.
Now all editorial are available.
We are sorry for a delay.
Dirty Vasya didn't clean the table in a year :D
Здравствуйте. Помогите пожалуйста, не могу понять решение задачи F. Откуда там берётся формула с суммой по всем множествам детей, почему там под суммой стоит произведение и как от этой формулы происходит переход к динамике, что нам даёт, что d[l, r]: = e[l - 1, r] и e[l, r] = d[l + 1, r]. Это же по сути одно условие?
На первом шаге найдём минимальное число b1 с суммой цифр a1. Далее, на i-м шаге найдём минимальное число bi с суммой цифр ai, которое больше чем bi - 1.Никак не могу понять обозначений. Почему "с суммой цифр a1", если суммы цифр у нас хранятся в последовательности b1..bn?
Есть ли решение задачи С по алгоритму из этого разбора на C++? Скиньте, пожалуйста.
http://codeforces.net/contest/509/submission/9667920
Прошу прощения, произошло переобозначение. Разбор считает, что последовательность a — это суммы цифр элементов последовательности b.
hmm....it is not important but my submission for 509C got accepted while it actually fails with a simple test case:
can someone please explain me the tutorial of pretty song in a more detailed way....I am unable to get what is written here!! :(