Прошёл очередной opencup, давайте обсуждать задачи.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
30:21:29
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
30:21:29
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 11:13:33 (f1).
Десктопная версия, переключиться на мобильную.
При поддержке
В I никто в спираль не поверил?
Мне задачи показались немного издевательскими.
Расскажите C и E.
E: Можно для каждого требуемого количества столов посчитать топ-200 клеток по целевому функционалу. После этого просто запустить поток на объединении этих клеток — понятно, что больше ничего нас не интересует.
Проблема в 1ом шаге, 25000000 сортировок 18 элементов даже близко не лезут в ТЛ. Поэтому надо использовать тот факт, что расстояния не сильно меняются при переходе в соседние клетки, т.е. если где-то сумма расстояний большая, то она большая и в какой-то окрестности. Впрочем, на java7 в ТЛ не лезет даже с этим (и ещё с кучей оптимизаций).
А, у тебя эта часть тормозит. Я делал так: переберем 2**18 подмножеств, для каждого найдём минимум суммы — это медиана по обеим координатам. Дальше для каждого размера n+k раз делаем следующее: берем минимальное расстояние, и добавляем в рассмотрение четыре соседние клетки. Ну и множество клеток в очереди на рассмотрении не имеет смысла делать больше n+k, так что храним их в куче по максимуму.
Другими словами, от 5000 моё решение не зависит (well, на самом деле зависит — я использовал битовый квадратный массив чтобы помнить, какие клетки я уже рассмотрел, но можно было бы и хешмэп).
А я вместо 2**18 подмножеств взял 18 * 18 точек, каждая медиана всегда в одной из этих точек, и их уже клал в очередь.
А после поиска медианы для каждого подмножества что именно мы делаем? То есть как запустить поток и что он должен считать?
Если смотреть по каждому x отдельно, то на самом деле сортировок можно сделать 5000 * 18 * 18, ибо сортировать имеет смысл, только в точках где значения для пары точек одинаковые. А еще можно заметить, что этими точками все разбилось на 182 отрезков и внутри функция монотонна, т.е. мы можем в каждом отрезке взять по 200 точек. В итоге вроде что-то гуманное получается.
В С если решать искать вероятность проигрыша вместо выигрыша, то получится простая динамика (сколько набрали, сколько шагов). Потом ответ просто 1 — p.
Выражаю особую признательность авторам задачи E и ТЛя к ней. Стандартный вопрос — есть ли решение на джаве? Я потратил полконтеста на упихивание (и последующее переписывание на плюсах). Особо доставило то, что плюсовое решение работало не быстрее джавовского на Java8, но на серверах кубка java8 недоступна (а у меня локально недоступна java7 — зачем держать старье у себя на компе), так что сравнить шансов не было.
Ну и ещё один традиционный вопрос — какие неправильные решения вы пытались отсечь таким ТЛем? Единственная приходящая в голову лажа — тупой стоимостной поток, но он бы и за день на таких ограничениях не доработал.
(после такого рода задач у меня появляются садистские мысли вроде подготовки контекста, в котором ничего не заходит без low level оптимизацией с использованием SSE и AVX. При этом желательно, чтобы на каком-нибудь левом языке вроде питона заходило без проблем с использованием читерских библиотек. После такого, наверное, авторы будут думать прежде чем ставить жёсткий ТЛ)
Решение на Java было. Около секунды работает. Обычное решение за 2^n * n + дейкстра на nk вершинах + поток на n + nk вершинах.
what could be the test 15 of E? I can't figure out what went wrong.
http://pastebin.com/sqDkRNg9
The answer is 806
That is weird. Because my code shows the exactly same output.In contest time it was shown WA on test 15. Anyway can i test my code or appeal? I think i missed the appeal time.
Your program prints 768 on server
У меня зашло на Java без единого TLя, но я скопипастил из какого-то старого контеста минкост с поиском кратчайшего пути дейкстрой без кучи за O(E+max_distance) (храня списки вершин на каждом расстоянии), может дело в этом.
А что, реально существенно обогнать в каких-то местах (ну, кроме умножения матриц) оптимизации gcc с правильными флагами под архитектуру? Конечно, флаги немного где ставят, но всё же.
Недавно же было на codeforces обсуждение, я там привел пример умножения матриц. Интересный челлендж — попробовать обогнать numpy.
Я, кстати, не знаю, насколько у нас на грани ТЛя зашло, но у меня был написан обычный поток со стоимостями с дейкстрой с TreeSet.
За 0.741с зашло.
Обсуждаю задачи: они были не очень. Не было даже ярко выраженных халяв, все какое-то упихивательное, чтобы участники вдоволь наобмазывались случаями.
Мне вот интересно, а заслать решений с разными вердиктами в яконтест можно было вчера? Все же знают, что в прошлый раз интерактивки тоже не работали.
В прошлый раз не запускался чекер. Сейчас проблема совсем другая. Система каким-то странным образом выдает вердикты.
По J всегда правильно выдавала WA. По H/I если интерактор возвращал WA, считала это за OK. Изменили код возврата интерактора с WA на CF, и правили вердикты ручками. Но на вашем решении вердикт интерактора полностью игнорировался. У ИТМО 1 было RE в J, но система выдавала WA.
В ejudge никаких пробелем с вердиктами я не заметил
А то. что мы сдали — это в итоге похоже на правду?
Сам код я не смотрел, но он проходит все тесты.
Забавно, что я в Я.контесте могу видеть stderr интерактора, в котором пишется ok/wa. Чтобы определить правильность решения, я открывал отчет, ctrl+f "ok ", далее если найдено 152 строк, значит се тесты пройдены.
Когда я вам убрал OK, у вас не работал только 1 тест, а в остальных было меньше 5000 запросов.
Ок, спасибо.
3 9 -1 10 5 10
Ждем 0.2 сек. Далее необходимо двигаться, так как грузовик будет накрывать точку (-1, 10). Освободит ее только через 1.8 сек. Это и есть ответ. Здесь скорость точки в 2 раза больше скорости грузовика, и она успевает сделать все: быстро отойти и пристроится сзади.
а тест #4 можно?:)
8 2 -5 6 4 8
А что в тесте #12?
В нем, вроде, выгодно подождать отрицательное время
В смысле выйти из точки (p, q) раньше, чем грузовик окажется в начальном положении?
Как решать G? Тернарник в бинарнике у нас не прошёл.
upd. проходит.
А бинарник в тернарнике зашел :)
Да, тоже уже сдалось. Мелочи там были.
Кто может объяснить B?
Есть ли решение C, более умное чем рандомно одним кубиком на малые градусы, вторым для поворотов и бегать на близком расстоянии от точки?
Ты про H видимо, а не про C?
Да, про H.
Утверждение: раскраска из sample input получает ОК
Доказательство: сабмит :) Ну то есть я взял это решение, промоделировал интерактор, на парочке случайных тестов убедлился, что такая стратегия работает и отсабмитил.
А, ну и еще — на каждой итерации используем тот кубик, который минимизирует матожидание расстояния до (0; 0)
В можно попробовать решить честно, перебрав много случаев, однако этого делать очень не хочется. Но если все-таки отважишься, то сперва лучше написать стресс, чтобы не искать баги до следующего ГП. Я написал стресс, который для каждой фигуры со сторонами от 3 до 50 и каждого вектора (пары точек) обновлял ответ. Ну вот если теперь выписать что у нас получилось в таблицу (для вектора), то можно увидеть закономерность. Получается очень хорошее решение в несколько строк, для которого у нас уже написан стресс :)
Придумали в D такое решение: для каждой клетки, содержащей отражатель, рассмотрим крест из строки и столбца, в которых эта клетка находится. Введем для каждого креста буловскую переменную, которая true если отражатель расположен одним способом, и false — если другим. Каждый шарик теперь, попадая в таблицу, оказывается в каком-то из крестов, притом никогда из него не уходит. Теперь для любой пары крестов определяем, в каком виде они могут сосуществовать (то есть, перебираем возможные расположения отражателей в них и смотрим, будет ли когда-нибудь столкновение шариков). Таким образом, мы свели задачу к 2-SAT. Но шариков до 10000. Каким образом можно быстро построить этот граф?
Заметим, что для зафиксированной пары отражателей есть всего две клетки, в которых могли столкнуться их шарики — это пересечение вертикалей и горизонталей, на которых эти отражатели лежат. Для шарика мы за O(1) можем узнать время, в которое он будет находиться в заданной клетке. Узнаем для каждого из шариков обоих отражателей, в какое время он будет в каждой из двух клеток пересечения, а потом проверим, что эти времени не совпадают. В итоге получается O(NM).
Также надо не забыть проверить, все ли хорошо для одного отражателя: не пересекаются ли шарики, летящие с вертикали и горизонтали: это так же делается за O(1) простой формулой.
Мы строили граф за квадрат от числа шариков.
Может кто-нибудь рассказать решение F?
Будем поддерживать такие числа, кроме двух чисел из ответа: для каждого типа помним, сколько его осталось за вычетом тех, которые мы уже точно знаем что проданы, а также для каждого значения t помним, сколько могло быть куплено игрушек с таким t, из тех, которые ещё не перешли в категорию "точно проданы", плюс для каждого значения t и количества помним, сколько есть типов с таким t и оставшимся количеством.
Каждый новый день появляется по 1 новой "могло быть куплено" для каждого t, плюс вычитается по одной "могло быть куплено" из тех, которые еще точно не определены, могли быть выкинуты в этот день, но не выкинуты. Из "могло быть" в "точно проданы" есть два перехода: либо когда игрушка физически исчезает из магазина, либо когда для какого-то суффикса значений t общее количество оставшихся игрушек с таким t равно количеству ещё не определённых дней, в которых обязательно продаются игрушки из этого суффикса.
В итоге получается решение за 10**5 * 100.
А расскажите, пожалуйста, решение J.
Найдем стратегию жюри. Стратегия — это перестановка. Рассмотрим пространство перестановок. Введем расстояние (pi, pj) = x, где pi — наша стратегия, pj — стратегия жюри, x — доля побед.
Ну и самая главная часть задачи: по данным перестановкам p1, p2, ... pk и расстояниям (p1, p * ), (p2, p * ), ..., (pk, p * ) найти наилучшее приближение p * . Я, например, это делал генетическим алгоритмом.
Интересно узнать решение задачи J из второго дивизиона.
Расскажите пожалуйста как нужно было решать задачу L. Performance (Div. 2).
Переберём все параболы. Найдём максимальное значение которое она достигает. Это происходит в точке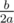
. Выведем номер параболы с наибольшим максимумом.
Здравствуйте. Кто решал второй дивизион, не подскажите, как решалась задача М (про крестики-нолики)? Вроде бы она изишная была, но, к сожалению даже с 16 раза не зашла(( Если решали, можете кодом поделиться?
Вроде всё сводится к тупому подсчёту числа случаев когда выиграют нолики и когда выиграют крестики.
Код сокомандника.
Cast Lo_R_D если что.
Спасибо)) Оказывается, нолики могут ходить первыми... странно
Is B, all about case analysis? Any easier way?
After some analysis, it comes up that there are actually only three significant cases:
1) Δ x or Δ y is equal to zero;
2) Δ x and Δ y have the same sign (both greater than 0 or both less than 0);
3) Δ x and Δ y have different signs.
Can't find upsolving again.
The letter-indexes of the problems in upsolving differs from letter-indexes in statements.
А в чем секрет последней задачи второго дивизиона?
Given that, there will be qualification round of deadline24, will there be opencup next week?