sophisticated1's blog

Shortest path using bfs
By sophisticated1, 10 years ago, In English

To find shortest path in a directed graph with edges having weight either 0 or 1 , we often use a modification of bfs with deque. But i don't know why we push at head of the queue whenever we encounter a 0-weight edge ?

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

https://www.hackerearth.com/alkhwarizm15/algorithm/completing-mario/

This problem explains the scenario better.

This problem appeared in alkhwarizm 2015. Although i solved it using dijkstra but as you mentioned that this problem can be solved using bfs by pushing the 0 weight edge at the head of the queue.

idea is very very simple. When you know explore level X in the bfs all the nodes which are level X-1 are already in queue right ? In this case from level X you might have explored level X again with an edge having weight 0 and then X+1 using edge with weight 1. putting the X level node at the end of queue will lead to inconsistency as there might be a scenario in the queue like this {X,X+1,X,X+1} (entries represents levels) but if you put the level explored through edge weight 0 it will not hinder the consistency in the queue and preforms desired work

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    thanks, can u give me a test case where this type of scenario occurs and where it becomes necessary to add 0-weight edge at the head of the queue ?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      Typical BFS never visits same nodes again so something like this should be nice example.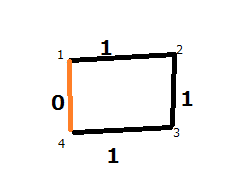

      You start in the node 1.

      After that you push node 2 and node 4 into your queue.

      After that you pop node 2 and push node 3.

      After that you pop node 4 and do not push node 3 again.

      You can optimize this by pushing 3 again with path relaxing way like if (d[3] < d[4] + 1) push(3)

      But it's not hard to prove that if you really do this there is a graph where your BFS will not work in O(E) complexity

      Hope this helps you.

      → Reply