On 26-March I had a coding round for Internship. Following were the 2 problems in that round :
Q1-> http://pastebin.com/KWjT8nJq
Q2-> http://pastebin.com/sa9VJkZF
My solution to question:
1-> http://pastebin.com/gzsDRNZK (RESULT : wrong answer)
In 2nd question naive solution gave TLE.
Can anyone please suggest new approaches or what test cases my code failed[Q1].
Thanks.











Fails for simple test case:
4
abab
baba
Answer = 1. Your output = 2
Also I think its a DP problem
Can you elaborate the DP solution ? I.e. How will you break this into subproblem ?
Also, bump.
For the first problem I think that the following greedy algorithm does the job but I am not sure. Please, correct me if I am wrong! :)
Loop over the positions and let's say that the current position is i (1 <= i <= N). If A[i]=B[i], then we can't change anything. Assume that A[i]!=B[i]. If there are no restrictions for both A[i] and B[i] (restriction means that it is said that A[i] or B[i] should be in the first or in the second string), then let's say that A[i] should be in the first string and B[i] should be in the second string. If there is a restriction for one of them make that the restriction is fulfilled (swap them if it is needed) and say that the other character (A[i] or B[i]) should be in its new positions. If there is a restriction for both of them, then try not to break it (it is possible only if the restrictions for A[i] and B[i] is for different strings). If it is impossible not to break the restriction, then try not to insert a new character in any string. Let's say that both A[i] and B[i] should be in the first string. If the character A[i] appears in the second string, the swap A[i] and B[i]. Otherwise, don't swap them
For example, let's take the strings "dir" and "rid".
For the first position there is no restriction for 'd' or 'r'. So let's say that 'd' should be in the first string and 'r' should be in the second string. Let's move to the second position. There are two equal characters so we can't change anything and skip it. Let's move to the third position. We should swap A[3] and B[3] since there is a restriction for both 'r' and 'd'. Now, we produced the strings "did" and "rir", so the answer should be 2.
No one talked about Q2 probably because it's simpler: for each iteration of i, try to determine the difference between number of comparisons and swaps you will do for that iteration. It's one of two possible values; now you only need to figure out when it's one and when it's the other.
Q1 looks more complicated, though. I don't know if there's anything simple I'm missing. Were there any constraints on the input strings A and B?
Second question is relatively easy. It can be solved binary indexed tree , binary search but both will be overkill. As we need to count the difference of comparison and swaps. Comparisons will be one more than the swaps if the number is not the current smallest otherwise it is equal.
Int calculate(int a[],int n){ Curr = inf ; Int ans = n ; For(int I=0;I<=n;I++){ If(curr > a[I]) ans --; Curr = min(curr,a[I]) ; Return ans ; }
If n is small (30-50) , we can also brute force through all the permutations in O(2^n).
Edit : my bad
Do you have any idea how much 2^50 is?
Anyway, the number of possible pairs is limited by the number of characters in the alphabet, so if latin letters are used you already have a 2^26 * 26^2 solution by testing the placement of all letters. The issue is that is really slow.
I think we can reduce it even more. Connect swappable characters with undirected edges, remove loops and parallel edges, and try to make this graph (of at most 26 edges) bipartite.
In this graph, for each odd-length cycle there should be at least one vertex to appear in both parts. I think we can select and remove minimal number of such vertices using greedy algorithm, and the rest is pretty simple.
"remove loops", did you mean self loops ?
Also how can be there at most 26 edges a->c..z, b->c..z , this configuration has more than 26 edges.
I assume I misunderstood something. Can you, please, clarify further, if possible with an example ?
yes
yeah, of course 26 vertices and at most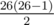 edges.
edges.
ok, consider two strings "dir" and "ird". Graph "d-i,i-r,r-d" contains an odd cycle "d-i-r", so we should remove any vertex ("d") and add 1 to the answer for both strings. New graph: "i-r". "i" goes to one part, "r" to another, and the final answer is "2-2".
I don't think its that easy. Consider "bcde" and "aaaa". Answer is 3 ("bcaa" and "aade"). But unless I misunderstand your graph idea you would put "a" in one string and "bcde" in the other.
I love how everyone throws greedy algorithms so easily without proof.
Odd cycle transversal is a well-known NP-complete problem.