k790alex's blog

[TJU — Stupid Problem] is there an alternative solution to suffix tree?
By k790alex, 10 years ago, In English

Hello, I'm trying to solve this problem (link).

A brief description:

Given two strings (s, t) and Q queries, each query contains an integer K, you should count how many substrings of s can be equal to t with changing exactly K characters of s.

constrains:
|s| <= 10^6
|s| > |t|
Q <= 10^5
characters can be 'x' or 'y' only

I got a solution using suffix tree which runs in linear time but my problem is that it uses too much memory.

I tried to reduce it to suffix array but I couldn't.

As the constrains are high I guess I need a linear time solution, can you see how to do it using less memory?

Thanks.

  • Vote: I like it
  • +8
  • Vote: I do not like it

»
10 years ago, # |
← Rev. 2   Vote: I like it +21 Vote: I do not like it

How did you solved this problem with suffix tree?

If we calculate hamming distance of small string with large string for every shifts, queries can be answered easily.

We can calculate those hamming distances with FFT. Overall complexity is O(NlogN)

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks but I didn't know how to compute these using FFT, can you explain a little?

    I'll try to describe my approach, let s = "xxyxx" and t = "xy", if I build the suffix tree for s (appending '$' as delimiter), I can traverse the tree with t counting the necessary changes to match them (see the picture).

    Each node have and id and the string contained in it, there are texts explaining the results, with this I can build an array containing how many substrings can be equal to t with 0 changes, 1 changes, .. , |t| changes.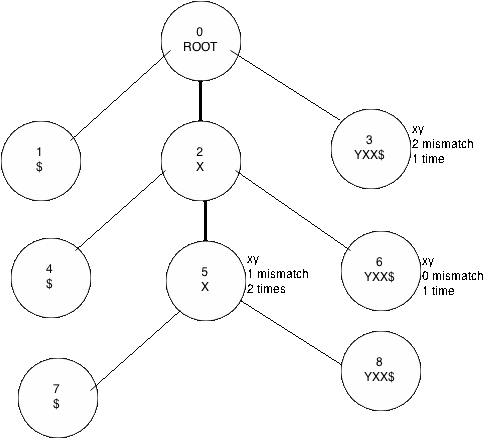

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      How are you calculating number of mismatches? As you know suffix tree is a compressed trie that's why there might be a node that holding information about thousands of characters. Are you able to do that step in constant time?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Yes, its a simple dfs like:

        // node is the current node of the tree the dfs is visiting
// index the current index of t
// mismatches is the number of mismatches I had found to get into the node
void dfs(node, index, mismatches) {
 if ( index == |t| ) {
  // means i traverse all t
  // count(node) = number of leafs of subtree rooted at node ( O(1) after preprocessing)
  // ans[x] = number of substrings of s that can be matched to t changing exactly x chars
  ans[mismatches] += count(node);
  ret;
 }
 // node contains a substring of s
 // node.begin is start index (inclusive)
 // node.end is end index (exclusive)
 for (i = node.begin; i < node.end && index < |t|; i++, index++) {
 // traverse substring at node until we reach end of t or end of node
  if ( s[i] == '$' )
   ret; // a delimiter means node has not enough chars to match t
  // count mismatches while traversing substring at node
  mismatched += s[i] == t[index] ? 1 : 0;
 }

 // traverse children
 for each children of node called next
  dfs(next, index, mismatched);

 // i had traversed the whole t
 if ( node is a leaf )
  ans[mismatched]++;
}
        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          You are not calculating mismatches in constant time, you are doing it in linear time. It will get tle anyway, even if we can handle memory issue.

          → Reply
          • »
            »
            »
            »
            »
            »
            10 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Is linear to |s| as far as I know, every vertex in the tree is going to be visited at most 1, it may be something I can't see, can you explain me why?

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              10 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              Please notice that your algorithm is same as simple brute force which is for each suffix do |S| comparsions. Which leads to overall O(|T||S|) complexity. There is no usage of suffix tree at all. Why do you even using it to travel on all suffixes? Only two loops would do the same!

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                10 years ago, # ^ |
                  Vote: I like it 0 Vote: I do not like it

                Whoops, I see it now.

                Thanks.

                → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      To calculate hamming distance with fft, one can create two polynomials where coficients is +1 for X and -1 for Y. Notice that if two characters is not same they will be counted as -1.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I can't see it but multiplying these polynomials is going to give the hamming distance for each substring of s? if yes, thats wonderful.

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          For each shift p denotes number of matches and q denotes number of mismatches.

          p+q = lenght of small string

          p-q = related coeficient coming from fft.

          So we know both p and q

          → Reply
          • »
            »
            »
            »
            »
            »
            10 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            I got an idea but I'm still confused, can you detail more your solution?

            Thanks.

            → Reply