kien_coi_1997's blog

What is the fastest way to find a circle given 3 point?
By kien_coi_1997, 10 years ago, In English

The task is classical. Given 3 points A, B, C, find a circle (I, R) that IA = IB = IC = R.

It is my solution.

  • First, calculate two midpoints of AB and AC.
  • Second, create two medians of AB and AC according to found midpoints.
  • Finally, find the intersection of the two lines.

The above solution forces me to declare a type named 'line' and write a boring code to find the intersection of two given lines.

I think that my solution is not the best. I want to find a better one.

Any suggestions would be appreciated.

  • Vote: I like it
  • +19
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it -66 Vote: I do not like it

The fastest way is to draw that circle.

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Looking at name of this blog entry, my first thought was about fastest in terms of number of operations, not in terms of coding :)

Maybe I am wrong, but it seems that solving geometry without using structures is not the best idea. Yeah, I also like to write pair<pair<int, int> ,pair<int, int> > stuff, but it is a bad habit :)

And what is so hard and boring in intersecting two lines? It is something like:

Point intersect(Line l1, Line l2) 
{
 if (parallel(l1,l2)) return Point(-1e100,-1e100);
 double det=l1.b*l2.a-l1.a*l2.b;
 double x=l1.c*l2.b-l1.b*l2.c;
 double y=l1.a*l2.c-l1.c*l2.a;
 return Point(x/det,y/det);
}

Or you may use vector <Point> instead, depending on which implementation of geometry is more comfortable for you and what is needed for given task (possible solution — one may return 2 points for same lines, 0 for parallel and 1 for intersecting).

Of course, I also would be glad to see some even better solution :)

→ Reply
»
10 years ago, # |
  Vote: I like it -21 Vote: I do not like it

You can calculate coordinate of point I at complex plane. To make equations easier, put A in 0.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it -40 Vote: I do not like it

    My teacher said, that calculating anything in geometry (or solving some equations) is a bad-style:( It's better to use functions like findPerpendicular and findIntersection.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 2   Vote: I like it -21 Vote: I do not like it

      Chto za dcp-autisti minusyat kazhdii comment v etom trede?

      → Reply
»
10 years ago, # |
  Vote: I like it +15 Vote: I do not like it

I faced this problem only once in my life — during last CH24 contest.

I have these two long lines from wikipedia in my solution:

xc = ((a.x * a.x + a.y * a.y) * (b.y - c.y) + (b.x * b.x + b.y * b.y) * (c.y - a.y) + (c.x * c.x + c.y * c.y) * (a.y - b.y)) / d;
yc = ((a.x * a.x + a.y * a.y) * (c.x - b.x) + (b.x * b.x + b.y * b.y) * (a.x - c.x) + (c.x * c.x + c.y * c.y) * (b.x - a.x)) / d;
→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    What is d?

    PS: found it.

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Thank you. I tried to follow the instruction in Wikipedia.

    I realized that moving A to (0, 0) makes the code shorter considerably.

    point center_from(double bx, double by, double cx, double cy) {
	double B=bx*bx+by*by, C=cx*cx+cy*cy, D=bx*cy-by*cx;
	return point((cy*B-by*C)/(2*D), (bx*C-cx*B)/(2*D));
}

circle circle_from(point A, point B, point C) {
	point I = center_from(B.X-A.X, B.Y-A.Y, C.X-A.X, C.Y-A.Y);
	return circle(I+A, abs(I));
}
    → Reply
»
10 years ago, # |
  Vote: I like it +21 Vote: I do not like it

If you want to calculate only R, then there is a compact formula: .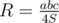

In your original approach, if you are intersecting medians, then you will get centroid, which is not the same, as center of circumscribed circle! Maybe you wanted to say perpendicular bisectors?)

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    My top priority is to find the center instead of the radius.

    Thank you for indicating my mistake. Google translate was wrong.

    → Reply
»
10 years ago, # |
← Rev. 9   Vote: I like it +24 Vote: I do not like it

Denote a = |BC|, b = |AC|, c = |AB|, .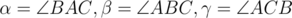

Then .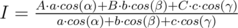

This is true since ray AI divides BC side at a ratio of b·cos(β) to c·cos(γ).

To avoid precision problems, you can use the equation a2 + b2 - 2ab·cos(γ) = c2.

→ Reply