A. Нужно было просто сделать то, что написано в условии. Единственный подводный камень в данной задаче - лидер может иметь отрицательное количество очков.
B. В данной задаче предполагается придумать оптимальную стратегию "зайцу", а затем просто симулировать игру.
Выигрышная стратегия для "зайца" - держаться от контролера подальше. А именно - в минуту движения поезда нужно отходить от него, если это возможно. В минуту остановки нужно переходить в вагон, до которого контролер доберется позже всего. Это всегда либо первый либо последний вагон поезда.
Так же можно было написать простенькое дп или классическую игру.
C. Назовем траекторией линию, которую описывает центр бильярдного шара во время своего движения. В начале своего движения шар выбирает одну из не более чем двух траекторий и движется по ней. Пусть общее количество траекторий равно k. Обозначит также максимальное количество попарно не бьющих друг друга шаров (ответ для нашей задачи) как z.
Теорема. z = k.
Доказательство. Каждый шар покрывает как минимум одну траекторию, а два различных шара не могут покрывать одну и ту же траекторию, иначе они будут бить друг друга. Значит z ≤ k.
Теперь покажем, как расставить k шаров так, чтобы они не били друг друга. Каждая клетка периметра принадлежит ровно одной траектории, а каждая траектория покрывает хотя бы одну клетку периметра. Значит, существуют k клеток на периметре, принадлежащие различным траекториям. Именно в них мы и поместим бильярдные шары. Конец доказательства.
Теорема дает конструктивный способ нахождения числа k --- для этого нужно просто посчитать количество компонент связности в графе, изображенном на картинке ниже. Это можно сделать с помощью BFS, DFS или системы непересекающихся множеств за время O(n + m).
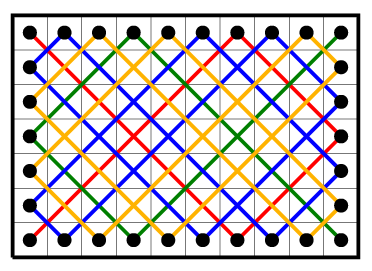
Например, на картинке 4 компоненты связности.
В данной задаче также есть решение в виде формулы: z = gcd(n - 1, m - 1) + 1. Можно было написать тупое решение и заметить эту формулу. Однако, доказать корректность такого решения несколько сложнее.
D. Заведем структуру данных, которая поддерживает быстрые операции добавления, поиска, извлечения любого элемента и поиска минимального элемента. Для этого, например, подойдет std::set в C++ или аналогичный контейнер в других языках. В этой структуре данных будем хранить отрезки пустых крючков так, чтобы извлечение минимума давало тот отрезок, в который нужно повесить пальто текущего сотрудника. Кроме того, для каждого сотрудника будем хранить отрезки пустых крючков, которые находятся непосредственно левее и правее.
С помощью этих структур можно за время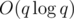 проэмулировать работу раздевалки. Сложности начинаются с ответами на запросы директора. Нужно как то быстро втавлять элементы в массив, удалять и отвечать на запрос суммы на отрезке.
проэмулировать работу раздевалки. Сложности начинаются с ответами на запросы директора. Нужно как то быстро втавлять элементы в массив, удалять и отвечать на запрос суммы на отрезке.
Онлайн решение. Для такого решения можно было написать какое нибудь балансированное или декартовое дерево.
Оффлайн решение. Сначала пройдемся по всем запросам из входа "в холостую" (то есть не отвечая на запросы директора) и сохраним все координаты, куда мы когда либо вешали пальто. Затем сожмем координаты и пройдемся по запросам второй раз. Теперь для подсчета сумм на отрезке можно использовать, например, дерево Фенвика.
E. Следующий набор команд позволяет поменять местами фишки на позициях 0 и 1: D1 R1 D1 L1 D1 R1 D1 L1 D1 R1 D1 L1 D1. Этот набор команд можно было найти либо на бумаге, либо используя двунаправленный BFS с ограничением количества допустимых ходов (на самом деле можно обойтись обычным BFS, если допустимые ходы ограничить очень сильно). Аналогичным образом можно менять местами любые две соседние фишки.
Теперь мы умеем менять местами два соседних элемента за 13 базовых операций. Дальнейшее решение строится тривиально и легко укладывается в ограничение в 10000 ходов.
B. В данной задаче предполагается придумать оптимальную стратегию "зайцу", а затем просто симулировать игру.
Выигрышная стратегия для "зайца" - держаться от контролера подальше. А именно - в минуту движения поезда нужно отходить от него, если это возможно. В минуту остановки нужно переходить в вагон, до которого контролер доберется позже всего. Это всегда либо первый либо последний вагон поезда.
Так же можно было написать простенькое дп или классическую игру.
C. Назовем траекторией линию, которую описывает центр бильярдного шара во время своего движения. В начале своего движения шар выбирает одну из не более чем двух траекторий и движется по ней. Пусть общее количество траекторий равно k. Обозначит также максимальное количество попарно не бьющих друг друга шаров (ответ для нашей задачи) как z.
Теорема. z = k.
Доказательство. Каждый шар покрывает как минимум одну траекторию, а два различных шара не могут покрывать одну и ту же траекторию, иначе они будут бить друг друга. Значит z ≤ k.
Теперь покажем, как расставить k шаров так, чтобы они не били друг друга. Каждая клетка периметра принадлежит ровно одной траектории, а каждая траектория покрывает хотя бы одну клетку периметра. Значит, существуют k клеток на периметре, принадлежащие различным траекториям. Именно в них мы и поместим бильярдные шары. Конец доказательства.
Теорема дает конструктивный способ нахождения числа k --- для этого нужно просто посчитать количество компонент связности в графе, изображенном на картинке ниже. Это можно сделать с помощью BFS, DFS или системы непересекающихся множеств за время O(n + m).

Например, на картинке 4 компоненты связности.
В данной задаче также есть решение в виде формулы: z = gcd(n - 1, m - 1) + 1. Можно было написать тупое решение и заметить эту формулу. Однако, доказать корректность такого решения несколько сложнее.
D. Заведем структуру данных, которая поддерживает быстрые операции добавления, поиска, извлечения любого элемента и поиска минимального элемента. Для этого, например, подойдет std::set в C++ или аналогичный контейнер в других языках. В этой структуре данных будем хранить отрезки пустых крючков так, чтобы извлечение минимума давало тот отрезок, в который нужно повесить пальто текущего сотрудника. Кроме того, для каждого сотрудника будем хранить отрезки пустых крючков, которые находятся непосредственно левее и правее.
С помощью этих структур можно за время
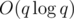 проэмулировать работу раздевалки. Сложности начинаются с ответами на запросы директора. Нужно как то быстро втавлять элементы в массив, удалять и отвечать на запрос суммы на отрезке.
проэмулировать работу раздевалки. Сложности начинаются с ответами на запросы директора. Нужно как то быстро втавлять элементы в массив, удалять и отвечать на запрос суммы на отрезке.Онлайн решение. Для такого решения можно было написать какое нибудь балансированное или декартовое дерево.
Оффлайн решение. Сначала пройдемся по всем запросам из входа "в холостую" (то есть не отвечая на запросы директора) и сохраним все координаты, куда мы когда либо вешали пальто. Затем сожмем координаты и пройдемся по запросам второй раз. Теперь для подсчета сумм на отрезке можно использовать, например, дерево Фенвика.
E. Следующий набор команд позволяет поменять местами фишки на позициях 0 и 1: D1 R1 D1 L1 D1 R1 D1 L1 D1 R1 D1 L1 D1. Этот набор команд можно было найти либо на бумаге, либо используя двунаправленный BFS с ограничением количества допустимых ходов (на самом деле можно обойтись обычным BFS, если допустимые ходы ограничить очень сильно). Аналогичным образом можно менять местами любые две соседние фишки.
Теперь мы умеем менять местами два соседних элемента за 13 базовых операций. Дальнейшее решение строится тривиально и легко укладывается в ограничение в 10000 ходов.











The problems are good
或许是出题人证不出来 :P
Видимо имеется в виду дерево отрезков, построенное как бы над массивом из 109 клеток. Явно все дерево не создается, хранятся только интересные вершины, в подотрезке которых что-то было или есть. А в указателях на все остальные вершины просто записан NULL.
UPD. Аналогичным образом понял почему работает дерево Фенвика на мапе.
In an nxn board , a ball starting from any point on a boundary comes backs to the same point without touching any other ball on the same boundary.
So , it's clear that nxn board is equivalent to nx1 board(for placing the balls) , in which case answer is n.
let a and b be the sides of board,
So if a > b keep on shrinking bxb blocks to bx1 block.
Code:
while( a > 1 && b > 1 ){
if( a > b) a = a - (b - 1);
else b = b - (a - 1);
}
return a + b - 1;
Say , in a x b grid with a > b "the boundary" is the left wall i.e 1st column.
Now trace the path of a ball travelling from from a point at "the boundary" back to some point on "the boundary". You will observe that ball goes and comes back from the same point at (a - b + 1)th column.
Hence , for tracing the paths in order to find conflicting points at "the boundary" we don't require columns farther that (a - b + 1)th column.
This is why we can say a = a - b + 1;
I still do not understand the relationship between this approach and the $$$\gcd(n-1,m-1)+1$$$ approach...
Great Work, absolutely correct! The key point in "reducing the size" was due to the "unchanged positional behaviour" of boundary of (txt) matrix as mentioned above, which is easily provable.
Moreover, a better/general visualization of the problem can be to tessellate the board in R2.
R2 D2 L2 U2 - переставить числа по треугольничку, причем из позиции 2,2 число поднимается наверх. Этого уже достаточно чтобы выстроить все кроме последнего ряда.
Дальше можно такими треугольничками и сдвиганием верхнего ряда переставить 1 2 3 в 3 1 2. Две таких перестановки и как раз получается обмен соседних клеток.