→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
6 дней
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
6 дней
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 25.11.2024 04:31:06 (h1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Почему долго не писал ничего? :)
Заболел
Не завтра, а послезавтра.
It looks like kutengine read the div1 250 statement and coded it in just seconds, submitting for 249.92 points. Impressive!
He and KUTcoder (who solved 500 under 3 minutes) have been banned. Good job, TC staff!
Now this is much closer but what do people think of Dshawn's submission in 1 minute 18 seconds? Looking at this code it seems hard to imagine that one could read the problem statement that fast and code the check function he has in so little time. But he is not banned so I guess unlike kutengine the topcoder admins think this is legit.
Hi, can someone explain div 1 500 approach? thnx
Let answer is 2a2·3a3·... (Notice that we should consider only primes ≤ 104) So we have to find ap for each p. Let α is maximal number such that pα ≤ n (linear multipliers will never be divided by bigger powers of p). Let's fix x modulo pα. Now for every multiplier (x - a) we can calc maximal r such that pr divides (x - a) for current x. Then we should find minimal sum of r-s among all possible values of x modulo pα. That approach is O(n3).
But it is easy to see that pr divides (x - a) only if x = a modulo pr. So, we can enumerate r and find d[r][i] — sum of powers (from the problem) of multipliers divisible by pr with x = i. And finaly for every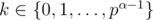 f(k) = d[0][k / pα - 1] + ... + d[α - 1][k]}. Min of f(k) is ap.
f(k) = d[0][k / pα - 1] + ... + d[α - 1][k]}. Min of f(k) is ap.
Lol, we couldn't enter rooms within 5 mins before start, so I deduced tht round is delayed. Moreover people were spamming chat with "delay!!!" messages, so I was convinced about it and so I returned to watching funny videos on YouTube. Few minutes later I returned and saw "Coding phase started" and learnt that I was 2-3 mins late -_-... What is more funny, I heavily struggled with hard and make it pass samples 25 secs before the end. And it passed systests :D! I thought that those lost 2-3 mins could be crucial for me, but it ended happily :).
Can someone please explain how to solve div2500 without greedy approach? binary search the answer maybe?
Here's how to binary search.
Suppose we want to check if we can make x rounds. Now, we already have E easy problems, so we need max(0,x-E) more easy problems. This can only come from easy/med problems. Similarly, we already have H hard problems, so we need max(0,x-H) more hard problems. This can only come from the med/hard problems.
So, we check EM >= max(0,x-E) and HM >= max(0,x-H). Now, we put everything else for the medium, so we also check that EM-max(0,x-E) + HM-max(0,x-H) + M >= x.
i get it! Thank you so much! :)
any help with Div2 1000 ?
any help with Div2 1000
EDIT: never mind it is already posted in TopCoder forums, thanks.
Расскажите div2 hard, пожалуйста, а то не получается зайти в разбор на топкодере(ошибку выдает при входе в личный кабинет).
upd: Времени прошло много, так что напомню условие: даны a, b, c в p(x) = ax^2 + bx + c; хотим найти 0 <= y < 10^9 такой, что p(y) кратно 10^9.