luckytoilet's blog

Data structure for special type of range query?
By luckytoilet, 10 years ago, In English

I was looking at the editorial for Round #300 Problem F, where you needed to count how many elements in a range is greater than k. The editorial stated "online data structures for this type of query are rather involved" and proceeds to describe a solution using the simpler Binary Indexed Tree.

Is there any known data structure that can efficiently query "how many elements in this range is greater than k"?

  • Vote: I like it
  • 0
  • Vote: I do not like it

Comments Comments (10)
| Write comment?
»
10 years ago, # |
  Vote: I like it +21 Vote: I do not like it

Segment Tree. In vertex we store sorted subarray using std::vector. Than, for find count of elements in segment [l, r] greater then k, we can do upper_bound in each of log(n) vertex, so complexity is O(log^2(n)) per query.

→ Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

If there is no update queries, persistent segment tree will do. per query.

Also, if you solve problem in offline BIT is enough.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    What if there are updates ?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      You can do it in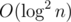 with segment tree which keeps the full interval in each vertex then.

      → Reply
»
10 years ago, # |
  Vote: I like it +6 Vote: I do not like it

u can also solve this problem using SQRT decomposition :)

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

you can also solve this problem using trie. I solved a similar problem using this approach where u need to find number of elements in range(l,r) which are <= k in each query.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +16 Vote: I do not like it

    How ?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      We can build a binary trie tree where at each node we store a vector containing the index of element of which that node is a part of.

      Something like this :

      For example we want to insert arr[10] = 5 and arr[11] = 2 in the trie. Let us consider all the elements in the array fits in 4 bits at max. So 5 = b(0101) and 2 = b(0010) in binary. We can build a trie like following in O(log2(maximum arr[i])).

      Visual representation :
      Insert Function :

      Now for the query portion i.e. finding number of elements greater than k in range l to r, what we can do is to count the number of elements less than or equal to k and then subtract it from total number of elements in range l to r to obtain our output.

      If we start traversing the binary representation of k from most significant bit to least significant we find the if ith bit of k is set then all the elements in trie with ith bit unset are less than k. So we can add the count of all indexes in the range l to r to the answer.If ith bit is unset then all elements with ith bit set are greater than k, so we ignore those elements. Following is a recursive function implementing the above idea.

      Count Function (<= k) :

      Here total(v) counts the number of elements >= l && <= r in the given vector v. It is defined as :

      upper_bound(v.begin(),v.end(),r) - lower_bound(v.begin(),v.end(),l)

      Finally you calculate answer as : r - l + 1 - cnt(root,l,r,k,(1<<30)))) assuming maximum element in array to fit in 30 bits.

      → Reply
»
7 years ago, # |
  Vote: I like it +1 Vote: I do not like it

For contests, If you need a good abtraction or if you want to learn a new merge-sort tree based datastructure for certain class of problem, Check this

→ Reply