542A - Здесь могла быть ваша реклама
Зафиксируем окно на телеканале и поймём, какой ролик имеет с ним наибольшее пересечение. Ролики бывают четырёх видов: вкладывающиеся в окно, накрывающие окно, частично пересекающие его слева и частично пересекающие справа. Научимся разбирать каждый вид.
Определить наличие накрывающего ролика просто — достаточно отсортировать ролики в порядке возрастания левой границы, и, идя по ним слева направо, поддерживать минимальную правую границу, достигнутую к текущему моменту. Если, проходя через окно j, мы видим, что текущее значение максимума не меньше, чем bj, то есть ролик, накрывающий наше окно, а значит ответ для данного окна можно установить равным (ri - li)·ci.
Среди всех вкладывающихся роликов надо найти тот, который имеет максимальную длину. Это можно сделать похожим образом, но чуть-чуть сложнее. Воспользуемся методом сканирующей прямой. Проходя через правую границу ролика ri, будем присваивать в некоторой структуре данных (например, дереве отрезков), значение ri - li в точку li. Проходя через правую границу окна, будем считать ответ для него как максимум на отрезке [aj, bj]. Таким образом мы учтём вложенные ролики.
Также можно определить наличие частично накрывающего ролика слева. Проходя через правую границу ролика ri, будем писать в точку li значение ri. Проходя через правую границу телеканала bj, посчитаем для него ответ как максимум на отрезке [aj, bj] минус aj.
Среди всех ответов для всех роликов выберем наиболее выгодный. Таким образом, выходит решение за  .
.
Упражнение А если веса есть не только на окнах, но и на роликах, и они перемножаются? Решите задачу за 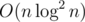 , получите виртуальную медаль!
, получите виртуальную медаль!
542B - Охота на уток
Будем приближаться к решению задачи постепенно. Во-первых, скажем, что у нас утки неподвижны, а охотник топает вправо со скоростью 1. Определим величину F[x][s] как минимальное количество уток среди тех, правые концы которых расположены не позже x, которых мы не сможем подстрелить, если последний выстрел был сделан ровно в точку s. В частности, в величину F[x][s] включены все утки, расположенные в отрезке [s + 1, x]. Значения F[x][s] для s > x будем считать неопределёнными.
Будем смотреть на F[x] как на функцию от s. Эта функция определена на всех s от 0 до x включительно. Ключевая идея заключается в исследовании того, как отличается F[x + 1][·] от F[x][·].
Давайте сначала предположим, что если в точке x + 1 не заканчивается ни одна утка, то в определении F[x + 1][·] фигурируют те же самые утки, что и в определении F[x][·]. Это значит, что все значения F[x][s] для s ≤ x остаются теми же. Интереснее дело обстоит с F[x + 1][x + 1]. Нетрудно видеть, что выстрел в точку x + 1 не может подбить ни одну из уток, заканчивающихся не правее x + 1 (так как мы только что предположили, что таких уток нет). Значит, F[x + 1][x + 1] = min F[x + 1][0... x + 1 - r] = min F[x][0... x + 1 - r].
Теперь давайте предположим, что в точке x + 1 заканчивается утка [l, x + 1]. В таком случае, можно смело сказать, что ко всем значениям D[x + 1][0... l - 1] можно прибавить 1 (потому что к моменту выстрела в точку s < l утку [l, x + 1] подбить ещё никак не возможно). В то же время, все значения D[x + 1][l... x + 1] останутся прежними, потому как последний выстрел и подобьёт новодобавленную утку.
Теперь давайте постепенно понимать реализационную сторону вопроса. Функция F[x][·] является кусочно-постоянной, а значит, её можно хранить в декартовом дереве в виде набора пар (начало отрезка, значение на отрезке). Такое хранение позволит нам легко прибавлять 1 на отрезке и брать минимум на префиксе функции.
Теперь будем считать, что функция F[x][·], определена на всей положительной полуоси, просто значения F[x][s] для s > x не удовлетворяют определению функции F[x][s]. Можно мысленно представить, что последний отрезок в структуре F[x] просто продляется до бесконечности вправо.
Будем идти сканирующей прямой по переменной x. Заметим, что функция F[x + 1][·] по сравнению с функцией F[x][·] меняется очень редко. Например, значение F[x + 1][x + 1] практически всегда совпадает с F[x][x + 1] (которое, в свою очередь, совпадает с F[x][x], о чём сказано абзацем выше). Действительно, в предположении, что в x + 1 не заканчивается ни одна утка, F[x][x] = min(F[x][0... x - r]) и F[x + 1][x + 1] = min(F[x + 1][0... x + 1 - r]) = min(F[x][0... x + 1 - r]) ≤ min(F[x][0... x - r]). Таким образом, интересное для нас событие возникает, когда значение F[x][x - r + 1] меньше всего префикса перед ним. Однако, величина min(F[x][0... x - r]) может не более n раз увеличиться на 1 (каждый раз, когда x проходит через правый конец утки), а значит, и уменьшиться может не более n раз (так как это неотрицательная величина).
Значит, событий вида "мы прошли через правый конец утки" и "нам надо нетривиально посчитать F[x][x] в сумме линейное количество. Каждое из них обрабатывается с помощью обращения к декартову дереву, которое происходит за  . А значит, мы получили решение, работающее за
. А значит, мы получили решение, работающее за  . Ура!
. Ура!
542C - Идемпотентная функция
Для решения этой задачи полезно разобраться, как выглядит граф, отвечающий функции из множества {1, ..., n} в себя. Рассмотрим граф на вершинах 1, ..., n, где из вершины i ведёт ребро в вершину f(i). Такой граф всегда выглядит как набор циклов, в которые ведут деревья. Как же должен выглядеть граф, отвечающий инволюции? Нетрудно понять, что в таком графе все циклы должны быть длины 1, а все вершины, которые не являются циклами длины 1 (т. е. неподвижными точками), должны сразу вести в какую-то неподвижную точку.
Значит, мы должны соблюсти два условия. Во-первых, все циклы должны стать длины 1 — для этого, как нетрудно понять, k должно делиться на [c1, c2, ..., cm], где ci — длины всех циклов. Во-вторых, все вершины, не лежащие на циклах, должны стать переходящими в вершины, лежащие на циклах. Иными словами, k должно быть не меньше, чем расстояние от любой вершины x до цикла, в которую она попадает (или, что то же самое, длины предпериода в последовательности f(x), f(f(x)), f(f(f(x))), ...).
Значит, наша задача свелась к тому, чтобы найти минимальное число k, делящееся на A, и не меньшее, чем B, что совсем несложно сделать.
Упражнение Какой максимальный ответ достигается в этой задаче? (Ответ: раз два)
Первым делом в этой задаче стоит разобраться, что из себя представляет функция Джокера. Одним из главных её свойств является мультипликативность: J(ab) = J(a)J(b) для (a, b) = 1, что даёт нам возможность записать значение функции, зная её значение на простых множителях аргумента: J(p1k1p2k2... pmkm) = J(p1k1)J(p2k2)... J(pmkm) = (p1k1 + 1)(p2k2 + 1)... (pmkm + 1). Воспользуемся этим знанием, чтобы решить задачу методом динамического программирования.
Обозначим за P множество тех простых чисел p, что скобка с их участием может встретиться в A = J(x). Таких простых немного — для каждого делителя d числа A он может соответствовать не более, чем одному простому, а именно, тому, чьей степенью является число d - 1 (если вообще является). Составим множество P, запомнив также для каждого простого числа p в нём, в каких степенях k скобка (pk + 1) делит A.
Теперь можно посчитать величину D[p][d], которая равна количеству способов получить делитель d числа A в виде произведения скобок от первых p простых чисел в множестве P. Такую величину можно посчитать методом динамического программирования за 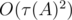 , где
, где 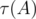 — количество делителей числа A (так как выше было показано, что
— количество делителей числа A (так как выше было показано, что 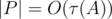 ). Значит, общая сложность решения —
). Значит, общая сложность решения — 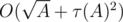 .
.
Упражнение Как себя ведёт 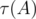 с ростом A? Например, какое максимальное значение
с ростом A? Например, какое максимальное значение 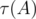 по всем A ≤ 1012? (Ответ:
по всем A ≤ 1012? (Ответ: 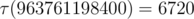 . Полезная оценка, не являющаяся, тем не менее, точной асимптотикой, заключается в том, что
. Полезная оценка, не являющаяся, тем не менее, точной асимптотикой, заключается в том, что 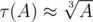 )
)
Упражнение А какой максимальный ответ достигается в этой задаче? Если получится сгенерировать тест, в котором ответ больше миллиона, с меня большой респект!
542E - Игра на графе
Заметим, что если исходный граф — недвудольный, то ответ — (-1). Действительно, любой нечётный цикл, будучи стянутым по паре вершин, всегда порождает нечётный цикл меньшего размера, в результате чего мы получим треугольник, с которым уже никак справиться нельзя.
С другой стороны, любую двудольную компоненту можно привести к виду цепочки, длина которой равна диаметру компоненты. Предположим, пара вершин (a, b) — диаметр некоторой компоненты связности. Тогда, стягивая все пары вершин, находящихся на одном расстоянии от a, как нетрудно видеть, мы получим требуемую цепочку.
Последним шагом остаётся заметить, что ответ — сумма ответов для отдельных компонент, которые можно по очереди подцепить друг другу. Таким образом, ответ — сумма диаметров компонент связности, если они все двудольные, иначе — (-1). Решение имеет сложность O(E + VE) (первое слагаемое — проверка на двудольность, второе слагаемое — подсчёт диаметра путём запуска BFS из каждой компоненты связности).
542F - Квест
Эту задачу можно было решать массой способов. Самый прямолинейный — динамическое программирование. Условие задачи можно переформулировать таким образом, что мы хотим выбрать какое-то множество вершин в качестве листов, для каждого потенциального листа известно верхнее ограничение на его глубину, и также известны стоимости каждого листа.
Будем идти по дереву снизу вверх. Посчитаем величину D[h][c] — максимальная возможная стоимость, которую можно получить, если, находясь на уровне h, мы имеем c вершин. Для перехода переберём, сколько листов именно имеющейся глубины мы возьмём (понятно, что из них выгоднее всего взять несколько максимальных), пусть, мы возьмём k. Тогда из этого состояния можно сделать переход в состояние D[h - 1][⌈(c + k) / 2⌉]. Ответ будет находиться в величине D[0][1] — действительно, придя на глубину 0, мы должны остаться с одной-единственной вершиной — корнем.
Сложность решения — O(n2T).
Упражнение Прокачайте решение выше до 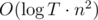 . А потом до
. А потом до 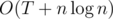











Ну вот, самое интересное на потом :(
Можешь быть уверен, он появится здесь раньше, чем Яндекс наладит свою тестирующую систему для тренировочного раунда Яндекс.алгоритма =)
Друзья, подскажите, пожалуйста! Никак не могу понять, почему моя программа 10986412 не прошла по времени. Я обнаружил, что все дело в посчете gcd и в таком виде 10991079 программа прошла тесты. Но почему она не проходила раньше? Подсчет gcd должен был пройти быстро, или дело в том что я использовал long long?
Думаю, что дело в
int nok. НОК в этой задаче может получиться слишком большой для инта, в результате чегоnokможет стать, например, отрицательным, но маленьким по абсолютному значению, из-за чегоwhile (res < ma) res += nok;выполняется целую вечность.Но я ведь как раз long long использовал, а в моих вычислениях и сам nok и все промежуточные величины из long long не выходят. Поэтому nok > 0, а так как ma <= 200, то
while (res < ma) res += nok;выполняется не долго. Проблема в том что сам gcd долго работает, по непонятной мне причине.Но сам
nok— этоint. Должно быть, Вы хотели сделать егоlong long, но ошиблись.Да обидная ошибка. Спасибо, что помогли найти :)
Я и сам, кстати, сегодня аналогично ошибся. :( Сумничал и написал
uint_least16_tв последней задаче, забыв, что интересность 1000 берётся не одна, а умножается на количество 1000, давая миллион.Подскажите, а как надо было искать в задаче D, степенью какого простого является d-1?
Есть такой метод: Переберем простые до корня, найдем наименьшее, на которое делится. Значит оно в какой-то степени и должна быть нашим числом.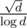
Это за
Но, видимо, у Zlobober есть более быстрый способ?
Можно же перебирать степень (их может быть лишь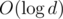 ), а потом за
), а потом за 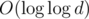 с double или за
с double или за 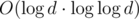 (бинпоиском) в целых числах проверять, подходит ли она.
(бинпоиском) в целых числах проверять, подходит ли она.
P. S. Множитель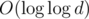 возникает из-за быстрого возведения в степень порядка
возникает из-за быстрого возведения в степень порядка 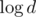 .
.
Но всё равно нужно же проверить, что найденное число будет простым. То есть в худшем случае всегда нужно проверять d — 1 на простоту
Действительно.
Но для чисел, меньших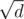 можно предпосчитать их простоту, а для больших можно проверять Миллером-Рабином. На асимптотику сильно не влияет, так как Миллер-Рабин запускается один раз.
можно предпосчитать их простоту, а для больших можно проверять Миллером-Рабином. На асимптотику сильно не влияет, так как Миллер-Рабин запускается один раз.
Хотя для d порядка 1012 выигрыш по времени не сильно велик.
Объяснение, почему наивная факторизация каждого d - 1 работает быстро, ниже в комментарии.
Сорри за поздний ответ, как-то упустил вопрос.
На этом контесте я столкнулся с неизвестной для меня ранее проблемой : размер бинарного файла был слишком велик, чтобы скомпилироватся (порядка 40мб). Я особого понятия не имею, что вообще такое бинарный файл и как посчитать его размер тем более не знаю, так что хотел спросить у кого-то, кто знает, как не наступить на эти же грабли еще раз. Как избежать слишком большого размера бинарного файла?
один из моих сабмитов
p.s. извините за оффтоп
Минимальный (почти) пример с проблемой: http://www.everfall.com/paste/id.php?d36vknsip9wh
Можно исправить так: http://www.everfall.com/paste/id.php?a7n4nwxt0r3z
Спасибо, разобрался.
About challange of problem A.
There are two cases.
We will choose two intervals [L1, R1], [L2, R2] where L1 ≤ L2 ≤ R2 ≤ R1. Lets find maximum value of this : (R2 - L2)C1C2, where C1, C2 are coefficients. To handle this case just use a segment tree which stores (R2 - L2)C2's and use same sweep algorithm. This part is O(NlogN).
This case is much more tricky. Again we will choose two intervals [L1, R1] and [L2, R2] where L1 ≤ L2 ≤ R1 ≤ R2. Then we will find the maximum value of this : (R1 - L2)C1C2. Imagine a 2D range tree that every node stores a segment tree and every node in segment tree stores a convex hull trick structure.:). We will insert lines y = mx + n where m = C1 and n = C1R1 to point (L1, R1) into the range tree. Building 2D range tree will be O(N(logN)2) and each query will be O((logN)2)(if we use two pointers technique in each convex hull trick structure)
Yes, exactly. Cool!
Если я нигде не ошибаюсь, то в F есть простое решение за O(NlogN), т.е. вообще независимое от T. Алгоритм аналогичен коду Хаффмана с небольшой модификацией (10987655).
I'm pretty sure I've seen problem C elsewhere before.
From solution of B, " In particular, the value F[x][s] includes all ducks located inside the segment [x + 1, s]. " I think you meant [s+1, x], am I right?
Yes, that was a mistype. Thanks.
Awesome problems! I liked the solution to E very much! Can anyone recommend some similar problems?
Можно пожалуйста поподробнее по D? Как именно искать величину D[p][d]?
"Let's denote as P the set of prime p such that the multiple including it may appear in A = J(x). There are not that many such primes: each divisor d of number A can correspond no more than one such prime, namely, the one whose power the number d - 1 is (if it is a prime power at all). "
How to calculate this set P (in problem D)? Doesn't it take lots of time to check if d-1 is a power of a prime? And this has to be done for all divisors d of A..
About checking probability : Miller-Rabin algorithm with T tests runs in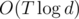 (assuming all arithmetic operations take O(1), which is true since A ≤ 1012) and makes an error with probability less than 4 - T. If T = 13 probability of error is basically non-existent.
(assuming all arithmetic operations take O(1), which is true since A ≤ 1012) and makes an error with probability less than 4 - T. If T = 13 probability of error is basically non-existent.
So to check whether d - 1 = pk, where p is prime and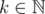 , you can iterate over possible values o k (there is
, you can iterate over possible values o k (there is 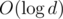 of them), calculate
of them), calculate 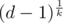 somehow (in doubles, for example), check whether it is integer and prime.
somehow (in doubles, for example), check whether it is integer and prime.
How do we check whether it is prime? We just precalculate all primes up to 106. If integer we are asked about is greater than 106, we run Miller-Rabin test else we return precalculated answer.
For any d we will run Miller-Rabin test only once: if k ≥ 2 then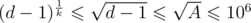 , so total time we need is about
, so total time we need is about 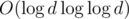 if we use fast exponentiation for integers.
if we use fast exponentiation for integers.
It is not necessary to use Miller-Rabin test. It's enough to just run normal factorization algo. It's pretty obvious that it can work efficiently since it almost impossible to create test where all divisors are pk + 1, but one can even prove an upper bound for this algo that shows that it works fast.
It works in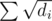 . Divide divisors in two groups: those who are small than
. Divide divisors in two groups: those who are small than  and those who are larger than
and those who are larger than  . Then you can estimate this sum as
. Then you can estimate this sum as 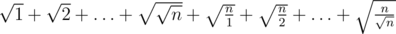 .
.
First summands are
summands are 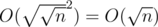 totally.
totally.
Last summands can be rewritten as
summands can be rewritten as 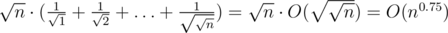 . It is about a billion, but if you substitute better estimation for
. It is about a billion, but if you substitute better estimation for 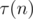 instead just
instead just  in last sum, then you'll see that it is even smaller:
in last sum, then you'll see that it is even smaller: 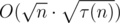 .
.
В задаче F, когда мы переходим в новое состояние, как мы берем несколько максимальных заданий? Ведь неизвестно, какие именно c элементов мы взяли.
Суть там в том, что любой ответ можно преобразовать в дерево определённого типа. А именно, если есть в ответе задание q, то дерево можно преобразовать так, что это задание будет висеть на высоте T — q.t. Поэтому мы для текущей высоты h, всегда выбираем среди таких заданий у которых T — q.t = h.
Разве в любом случае мы можем так преобразовать? Например, у нас 3 задания с уровнем, скажем, 4. Как у нас может быть 3 листа на уровне 4?
Если ещё актуально.
Построим полное бинарное дерево с 4 уровнями. Поместим те вопросы вниз. Затерём всё лишнее.
В общем случае как-то так. Пусть у нас есть ответ-дерево. Приведём его к нашему виду и покажем, что всё ещё можно ответить на все вопросы за <= T минут. Пусть для всех уровней <= k мы уже преобразовали. Покажем для k + 1. Очевидно что все листья, у которых ограничение T — q.t = k + 1, сейчас находятся именно на этой высоте. Не трогаем их. Посмотрим есть ли там листья иные. Опустим эти листья ниже (то есть сделаем из листа вершину, и пустим две ветки и поместим туда лист). Очевидно что всё ещё можно ответить на все вопросы, так как каждый лист находится на высоте, не превышающей ограничение. Дальше по индукции.
Could someone explain why: "Indeed, if we suppose that there is no duck ending in x + 1 then F[x][x] = min(F[x][0... x - r])" is true? Isn't this only the case if there is no duck ending at x?
EDIT: This is for problem B.