I had a question that suppose we have 2 or n piles like normal standard game and in one turn a player can either pick from one of them any number of things or equal amount from all the piles.Change is player 1 is given m turns to skip and player 2 is given n turns to skip.The number of things in each pile is given.Who will be the player if both players play optimally?
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
28:26:12
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
28:26:12
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 13:08:50 (i2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











I assume the number of piles n is unrelated to the number of turns n Player 2 may skip. In fact, let's disregard the number of piles altogether; Player 1 can skip m turns while Player 2 can skip n turns.
By using combinatorial game theory, the "normal game" (which appears to be some variant of Wythoff's game that allows you to either take from one pile or take an equal number from all piles) is an impartial game, and thus by Sprague–Grundy theorem is equivalent to a nimber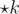 . Adding m for the number of turns Player 1 has, and - n for the number of turns Player 2 has, gives our game an evaluation of
. Adding m for the number of turns Player 1 has, and - n for the number of turns Player 2 has, gives our game an evaluation of 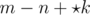 . It is known that
. It is known that 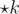 is greater than any negative number and less than any positive number; thus, if m - n > 0, since
is greater than any negative number and less than any positive number; thus, if m - n > 0, since 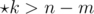 we have
we have 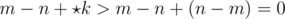 which tells Player 1 will win, while if m - n < 0, since
which tells Player 1 will win, while if m - n < 0, since 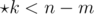 we have
we have 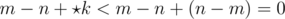 which tells Player 2 will win. If m - n = 0, then our game is simply
which tells Player 2 will win. If m - n = 0, then our game is simply 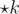 ; both players can ignore their extra turns.
; both players can ignore their extra turns.
What this means, in layman's terms, is this: the original game is won by either the first player (the player to move) or the second player (the player that has just moved). Because both players have the same moves at all times, there is no difference between Player 1 and Player 2 besides that one starts the game. If m > n, Player 1 gets the choice; he can either play as the first player, ignoring his extra move, or play as the second player, skipping his first turn. Whenever Player 2 skips a turn, Player 1 simply skips another turn as well. This guarantees a win for Player 1. Likewise if m < n, but now the win is for Player 2. On the other hand, if m = n, they both can ignore the extra turns; the winning player shouldn't use it (when he plays perfectly, he should always have winning positions; skipping a turn would pass the winning position to the opponent), while if the losing player uses it, the winning player simply undoes that by skipping his turn as well.
So allowing a number of skipped turns doesn't add any complexity at all, besides a simple O(1)-comparisons check at the beginning.