Скоро начнётся квалификационный раунд Яндекс.Алгоритм 2015. Это последняя возможность для тех, кто не участвовал в тренировочном раунде или не решил в нём ни одной задачи, пройти на отборочные раунды, которые состоятся 24 и 30 мая и 6 июня.
Сам квалификационный раунд продлится 100 минут и пройдёт в виде виртуального контеста: каждый участник сам может выбрать время начала в периоде между 17 мая 0:00 и 18 мая 0:00 МСК. Это значит, что некоторые участники потенциально смогут продолжать участвовать до 1:40 МСК, поэтому не стоит обсуждать задачи до этого времени. Для прохождения в отборочный раунд необходимо решить хотя бы одну задачу.
I started the contest, but problem statements seem to be unavailable. Instead of problem statements, there is just text "Problem statement is unavailable".
edit: All problem statements are now available in english.
Same here. I can only read problem D and F but only in russian...
i am also facing same problem and my time counting already started
Yeah me too, but the clock doesn't stops ticking.
WESLEY SNEIJDER & GALATASARAY! CHAMPIONS
To advance to the elimination round, it is necessary to solve at least one problem.
Is it also sufficient to advance by solving only one problem?
Вот в правилах сказано:
То есть получается, чем в большем количестве раундов ты участвовал, тем лучше? Как-то это странно. Или можно участвовать в одном раунде? Не все же могут поучаствовать в утреннем раунде.
Можно. Но, поскольку учитывается сумма, если ты не tourist, шансы пройти будут не очень большие. Поэтому рекомендуется участвовать во всех трёх раундах, в том числе и в утреннем.
Да в этом и вопрос. Но меня не интересует топ-30 и очки, а топ-512. Как они определяются? То есть вначале идут люди с очками, а потом без очков. И те кто без очков сортируются по количеству задач?
Участники сортируются по сумме очков, потом по количеству задач (в сумме по трём раундам), потом по штрафному времени (опять же, в сумме).
My first submission stayed with the "waiting" status for about half an hour and I had a stupid bug that I had to wait half an hour to correct. I hope this doesn't happen in the Elimination rounds.
Also, the scoreboard was not live but updated every few minutes. I could not see my new position immediately after getting a problem Accepted.
How can I change my country (in the standings etc)? It says that I'm from USA and I can't find how to change it. I haven't put "USA" to anywhere.
Расскажите, пожалуйста, как решать B.
Бинарный поиск по ответу. Зафиксировали какой-то максимальный вес. Добавили все ребра Ui которых не превышает зафиксированного веса. Затем построим конденсацию данного графа и посчитаем степени захода для каждой компоненты. Пусть c1 — количество компонент, у которых степень исхода = 0, а c2 — у которых степень захода = 0. Тогда можно получить ответ с зафиксированным весом только в том случае, если max(c1, c2) <= 1
Code Here
Хм,работает ли это на графе
?
Ответ -1
И правда, не работает :) Скорее всего, weak tests.
Я проверяю, что конденсация — бамбук и ловлю ва2. Спс, бросил дебажить.
против бамбука будет
1 2 1 1 3 1 2 3 1
Да это работает, я погорячился с понятием бамбук, имел в виду, что в топсорте есть рёбра между соседними.
После сжатия компонент на самом деле нужно проверить, что они образуют цепочку (возможно с дополнительными ребрами)
Собственно, явно строить конденсацию не нужно. Я использовал алгоритм, который обходит компоненты сильной связности в порядке топологической сортировки, и для каждой компоненты, кроме первой, проверял, что в неё входит ребро из предыдущей компоненты.
А был еще кто-нибудь кто подумал, что надо минимизировать сумму? Есть соображения, что с ней вообще можно в таком случае делать?
Ничего. Это NP-трудная задача.
И в продолжение темы — я пол контеста думал, что ребра, которые не указаны, имеют вес 0. Кто-то умеет решать такое при заданных ограничениях?
Вроде как я умею.
Для такой задачи достаточно в самом начале слегка сжать компоненты сильной связности на графе из нулевых ребер, потом добавить O(M) нулевых ребер, таких, что обратное ребро имеет ненулевой вес, а дальше решать как задачу с контеста.
Сжатие компонент можно делать следующим образом: Будем поддерживать вершины отсортированными по сумме количеств исходящих и входящих ненулевых ребер. На каждом шаге берем первую такую вершину, для нее находим любую вершину с которой она не связана ни в какой сторону, сливаем с ней текущую вершину, обновляем ребра.
Так как мы будем каждый раз мэрджить меньшую вершину к большей, то каждое ребро будет слито не более чем логарифм раз. В итоге выйдет что-то около
Похоже на правду. А если держать списки рёбер в хешсетах, то вообще будет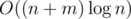
. Здесь 
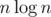— стоимость поддержки кучи из n вершин, а 
— стоимость слияния, если стоимость слияния двух вершин имеет порядок количества рёбер из меньшей вершины. Остаётся вопрос: как быстро искать вершину, в которую из данной нет ребра? Утверждается, что если просто перебирать номера всех оставшихся вершин по порядку, то количество неудачных попыток будет не больше, чем количество рёбер из вершины, а это число уже заложено в сложность.
А зачем отсортированность поддерживать?
Построим неориентированный граф по ориентированному(убрав ориентацию ребер). Потом решим задачу 190E - Контрнаступление (не реклама!:) ) за
O(n + m). Те вершины, что в одной компоненте будут в одной КСС по 0-ребрам.Далее осталось не более
O(sqrt(m))вершин, а значит если удалить повторяющиеся ребра, то можно явно провести все 0-ребра(их будет O(m)), далее можно решать как обычноWhat's the solution for "Optimal Playlist"?
My Unaccepted Solution:
f(x) -> returns if graph with edges that cost at most x can make a playlist.
It uses binary search to find the least x such that f(x) is true, which is the answer.
My Implementation
That is incorrect because of this test case: (the edges)
1 2
1 3
there isnt a walk that goes to 2 and three so yeah ofc you'll get werong answer
Can you elaborate a little bit? I think my algorithm works for this case.
give me a walk that crosses vertex number 2 and vertex number 3 it is impossible because you can't get out from either 2 or 3
I know. it's impossible according to my algorithm too. It first removes 1 because it has a in-degree of 0. With the removal of 1st vertex, both vertices (2 and 3) start to have 0 in-degree. Since there are more than one vertex that has a in-degree of 0, there isn't any walk that visits every vertex at least once.
Oh Lol sorry i didn't know Kahn's algorithm, anyway i think if you check if the i'th component is connected to the i+1'th it get's accepted
You need to clear adj2 after every call to f().
Thank you!