Привет, CodeForces!
Время от времени на CodeForces появляются вопросы о центре, радиусе и диаметре графа (смог нагуглить только о дереве, хотя было больше). В этом топике даны определения этим понятиям а также описаны алгоритмы для их нахождения.
Задача: дан не взвешенный неориентированный граф G = (V, E), где V это множество вершин, а E — множество ребер. Необходимо найти его радиус, диаметр и центр.
Определим di, j как кратчайшее расстояние между парой вершин 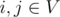 . Тогда диаметр графа определяется как максимально возможное среди всех кратчайших расстояний между парой вершин:
. Тогда диаметр графа определяется как максимально возможное среди всех кратчайших расстояний между парой вершин:
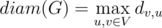
Также введем понятие эксцентриситета вершины как максимальное расстояние от вершины до какой-либо другой:
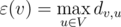
Зная эксцентриситет всех вершин, можно определить и радиус графа, как минимальный из них:
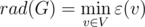
Сразу можно заметить, что диаметр графа это максимальный эксцентриситет в графе, т.е:
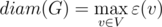
Центром графа назовем все вершины с эксцентриситетом, равным радиусу графа:
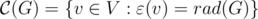
Определения даны и в голову приходит тривиальный алгоритм для нахождения центра, радиуса и диаметра для произвольного графа при помощи алгоритма Флойда-Уоршелла:
const int N = ...; // Количество вершин в графе
const int INF = ...; // Бесконечность
int d[N][N]; // Дистанции в графе
int e[N]; // Эксцентриситет вершин
set <int> c; // Центр графа
int rad = INF; // Радиус графа
int diam; // Диаметр графа
// Алгоритм Флойда-Уоршелла
for (int k = 0; k < N; k++) {
for (int j = 0; j < N; j++) {
for (int i = 0; i < N; i++) {
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
// Нахождение эксцентриситета
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
e[i] = max(e[i], d[i][j]);
}
}
// Нахождение диаметра и радиуса
for (int i = 0; i < n; i++) {
rad = min(rad, e[i]);
diam = max(diam, e[i]);
}
for (int i = 0; i < n; i++) {
if (e[i] == rad) {
c.insert(i);
}
}
Теперь немного изменим постановку задачи: допустим, что граф G является деревом. Для дерева несложно доказать следующий факт: количество вершин в центре дерева равно одному или двум.
На CodeForces когда-то слышал следующий алгоритм для нахождения центра дерева: с помощью BFS-а из любой вершины (обозначим ее как v1) найти самую удаленную от v1 вершину (обозначим как v2), затем запустить BFS из v2, выбрать любую самую удаленную от v2 вершину (пусть будет v3). Вершина(-ы) на середине пути между v2 и v3 образуют центр графа, расстояние между ними — диаметр. Радиусом же будет половина диаметра, округленная вверх: (diam(G) + 1) / 2. Реализацию этого алгоритма здесь приводить не буду, так как она мне показалась несколько громоздкой. Вместо этого приведу другой алгоритм, который мне показался проще в реализации.
Теорема: Пусть L — множество всех листьев графа. Если |V| ≤ 2, то L является центром графа, иначе можно удалить все листья и центр графа не изменится:
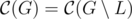
Эта теорема приводит нас к следующему алгоритму: будем удалять листья дерева, слой за слоем, пока не останется ≤ 2 вершин. Эти вершины и будут центром графа. Реализация данного алгоритма очень похожа на поиск в ширину:
const int N = ...; // Количество вершин в графе
int maxlevel = 0; // Уровень, на котором будет расположен центр графа
int level[N]; // Уровень вершины
int degree[N]; // Степень вершины
int g[N][N]; // Матрица смежности
set <int> c; // Центр графа
queue <int> q; // Очередь для алгоритма
// Начинаем с листьев
for (int i = 0; i < N; i++) {
if (degree[i] == 1) {
q.push(i);
}
}
while (!q.empty()) {
int v = q.front();
q.pop();
// Удаляем лист и пытаемся добавить его предка
for (int i = 0; i < N; i++) {
if (g[v][i]) {
degree[i]--;
if (degree[i] == 1) {
q.push(i);
level[i] = level[v] + 1;
maxlevel = max(maxlevel, level[i]);
}
}
}
}
for (int i = 0; i < N; i++) {
if (level[i] == maxlevel) {
c.insert(i);
}
}
Нетрудно доказать, что после исполнения данного алгоритма, центр дерева будет во множестве c, 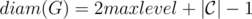 и rad(G) = (diam(G) + 1) / 2.
и rad(G) = (diam(G) + 1) / 2.
Задачек на порешать сходу не нашел, так что если знаете — ждем в комментах.
Задачки по теме:
Спасибо за внимание, насчет опечаток просьба писать в личку.











Задачка: IOI2013 Dreaming
Great post, here are some problems to solve:
Dreaming IOI 2013 Day 1
Civilization
Как для дерева найти кол-во пар вершин таких, что расстояния между ними равняются диаметру?
Найдем центр дерева, как описано с статье. Из каждой вершины в центре дерева запустим дфс, который для вершины подсчитает количество листьев в нем, находящихся на максимальном расстоянии от него. Обозначим это число как
leafs[v].Получаем 2 случая:
1) В центре дерева две вершины, тогда ответ
leafs[a] * leafs[b], гдеaиb— вершины, входящие в центр.2) В центре дерева одна вершина (обозначим ее как
a). Тогда ответ можно посчитать следующим образом:x
|
x
|
a — x
|
b — x
|
x
|
x
Для этого дерева ответ 1, но здесь leafs[a] = 2 и leafs[b] = 2, а leafs[a] * leafs[b] = 4. Ответы не совпадают!
Я что-то не понял твоего теста.Если это цепочка, то вершиныaиbне являются центром.Правильный тест во второй правке.
Да, я понял, немного поторопился с ответом, и недосказал.
leafs[v]— это количество листьев в поддереве вершиныv, находящихся на максимальном расстоянии отv. То есть в твоем тестеleafs[a] = 1,leafs[b] = 1. Сейчас поправлю коммент.Ок, в код вкралась небольшая ошибка, поправил ее
Ну все-таки не число листьев нам надо посчитать, а число листьев на расстоянии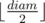 от центра.
от центра.
Опередили на пару секунд буквально :)
Some problems related to this acticle:
322E — Ciel the Commander
592D — Super M
Added them into post.
322E - Командир Ciel seems to be not about center of a tree, but about centroid of a tree (proof)
Sorry, that was my mistake.
http://codeforces.net/gym/100279/attachments/download/2025/20122013-international-open-olympiad-kpiopen-2013-round-1-en.pdf Problem F here
Thank you, added to the post.
Спасибо.
Всегда использовал 2 дфса. Теперь наверное буду писать как у Вас.
Isn't it NP-Complete to find graph diameter in random graphs? Since you'd have to solve the longest path problem.
Nope — diameter is longest among all shortest paths (Graph Diameter).
Oh, my bad. The post said :
" Let's denote d(i, j) as distance between nodes i,j. Then diameter of graph is denoted as the greatest possible distance between two nodes. "
I didn't understand it meant shortest paths.
I'll fix that.
I can prove that this algo is correct in acyclic graph.
But, will this algo working in cyclic graph?
If you are talking about finding everything using Floyd-Warshall's algorithm it should be correct for any graph.
The second algorithm works only for trees. Citation:
Now let's try to change problem statement: suppose that G is a tree.I was talking about second algorithm.
Oh, I didn't notice that sentence >< Thanks for replying.
Does the center algorithm work when the tree edges have weight?
TLE'16 December Contest — Christmas Tree Building Another problem related to this article