Hi!
Did you know 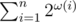 is O(nlogn)? (ω(n) is the number of distinct prime divisors of n)
is O(nlogn)? (ω(n) is the number of distinct prime divisors of n)

I wonder why! Do you have any mathematical proof for this?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | adamant | 151 |
| 7 | djm03178 | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/23/2025 23:10:45 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Because 2w(i) ≤ d(i) (d(n) is the number of divisors of n), so this is less than sum of d(i), which is the number of pairs i, j such that j divides i, which is sum of n/j, which is O(nlogn).
At the first look I was totally surprised about this fact, but it sounds easy when you say it like that!
Thanks!
it's nice information, do you know any problems that can be solved using it?
It's one of training tasks for our national OI (INOI):
Consider a n × n forest. For each relatively prime pair (i, j)i, j ≤ n, we plant a tree on position (i, j). The problem is to calculate total sum of pairwise distances between trees!
n ≤ 106, distance((a, b), (c, d)) = |a - c| + |b - d|
Also you can use that fact for this problem.
I don't think that much theoretically about problem, since each number lower than 10^6 has at most 7 distinct prime divisor, we can perform 2^7 * 10^6 :D This problem is much like SGU 370
Yes, but it's always good to know the exact complexity of our solution! (Without considering the limits)
What about lower bound? I can prove just Ω(nloglogn)
Lower bound:
Let Pn be a set of primes not larger than n.