Всем привет!
Может кто-нибудь где-нибудь видел задачу, в которой нужно поддерживать лес деревьев и делать на нем какие-то операции? Например, задача в которой требуется поддерживать следующие операции:
Подвесить одно дерево к вершине другого
Удалить ребро
Сказать, находятся ли две вершины в одном дереве (или какой-нибудь другой запрос)
Может кто-нибудь знает, как можно решать такую задачу, кроме как с помощью link-cut tree или хранения обходов деревьев в декартовых деревьях?
Буду очень благодарен за ссылки на задачи и мысли по поводу того, как проще всего такое решать!











Можно забыть про то, что это деревья, получить задачу dynamic connectivity, взять диплом Burunduk1.
Скажем, есть очень простое offline решение с СНМ: сказали, что каждое ребро живёт в течение некоторого времени, построили дерево отрезков по времени, каждое ребро попало в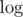 вершин, обошли dfs'ом.
вершин, обошли dfs'ом.
Если же хотеть считать что-то на путях, то ничего проще heavy-light/link-cut trees/Euler tour trees я не знаю.
О, решение с СНМ в оффлайне это круто, я про него забыл.
Глобально хочется считать что-то на путях, да. А так, я просто пытаюсь писать диплом про динамические деревья, которые могут почти все тоже самое, что и link-cut и пытаюсь найти какую-нибудь простую задачу, чтобы можно было легко потестить:)
Если нужно протестить, то вот примерно такая же задача как в блоге, третий запрос — расстояние между вершинами.
На недавнем тимусе задача просто сводится к твоей, по модулю того, что запрос про связность вообще, а не про две вершины. Хотя не уверен, что это авторское решение :)
Я не умею сводить. Там вроде бы не лес получается.
SRM #631 hard
SRM #624 hard
А как вообще это решается через хранение обхода?
Ну т.е. я понимаю общую идею (храним эйлеров обход в сбалансированном дереве поиска, склеиваем/расклеиваем его при необходимости), но не понимаю, как быстро по вершине найти дерево, в которм она хранится. Это как-то отдельно поддерживается?
Можно по вершине графа быстро найти соответствующую ей вершину в сбалансированном дереве поиска. Скажем, хэш-таблицей, массивом, просто хранить указатель на вершину дерева в структуре "вершина графа" или вообще сказать, что это одна и та же структура.
А дальше есть задача "по вершине сбалансированного дерева понять, что это за дерево". Обычно для понимания "что за дерево" достаточно найти корень, а всю нужную информацию в нём хранить. Можно хранить в каждой вершине дерева ссылку на родителя и за глубину сбалансированного дерева находить корень, прыгая по ссылкам вверх от произвольной вершины.