Всем привет!
Завтра в 14:00 MSK состоится очередной Topcoder SRM 660.
Предлагаю обсудить задачи после контеста!
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Всем привет!
Завтра в 14:00 MSK состоится очередной Topcoder SRM 660.
Предлагаю обсудить задачи после контеста!
| Название |
|---|



Match starts in less than an hour.
What was the idea behind Div1|B?
First of all use linearity of expected value. So for each elem we should know its probability to be on the event.
Then go from him and you'll get cycle(maybe of 1 element) and precycle.(each of them <= 50) so there are no more than 50*50 dp states.
Then just chose chose among those the first who was asked to go, and you will get similar subproblem
It can be solved in O(N) and I solved it (in practice rooms) pretty much that way. It turns out that the DP equates to adding/subtracting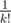 for each person, where k is up to the number of times we can iterate
for each person, where k is up to the number of times we can iterate  before finding a cycle.
before finding a cycle.
why is it so? could you provide more details on it?
Assume that you put person i in place j1. This person will accept the invite in (N - 1)! permutations minus (number of permutations where person A[i] accepts and is in a place j2 < j1). For a fixed j2, the part in brackets can be rewritten similarly as (N - 2)! — number of permutations where A[A[i]] is in a place j3 < j2 < j1 and accepts, etc. When you iterate A[A[A[i]]]..., you reach a cycle at some point — and in that case, you want to count the number of permutations where the people i, A[i], A[A[i]]... alternately accept and don't accept invitations; that case is trivial, since the person you cycled to always declines the invitation. The full form of the sum you get is , where S(N, k) is the number of decreasing sequences jk, jk - 1, .., j1, the number of times you can add (N - k)! in the approach above — which is actually the binomial coefficient C(N, k), and you want to sum up
, where S(N, k) is the number of decreasing sequences jk, jk - 1, .., j1, the number of times you can add (N - k)! in the approach above — which is actually the binomial coefficient C(N, k), and you want to sum up  for k from 1 to the number of people you iterated through before reaching the cycle (where the sum terminates).
for k from 1 to the number of people you iterated through before reaching the cycle (where the sum terminates).
This counted the number of permutations where i accepts the invitation; sum up for all people and divide by N! to get the expected value.
almost all of div2hard's submission have been hacked lol
Pretest are so weak, many people do not even try their code on max test. BTW, what is solution to that problem?
I have seen the similar problem may be in Hackerrank or UVA don't know exactly, but I did not read the solution. In that problem as far as I remember instead of 1 to n , you have to find for particular n ^ k under some mod, and k is something like 10^100 something.
I solved in the contest using BigInteger but after testing find its too slow.
Iterate for every i from 1 to n. If i is a prime, then get answer for that i in O(k), else it is a composite number, which means solution for that i can be expressed as multiplication of some other two solutions less than i, and we already have that. You can use sieve of Eratosthenes to test if some number is a prime, or to get some factor for that number if it isn't. Complexity: pi(n)*k + n*ln(n)
I think I overkilled, but...
Since i2k = (i2k - 1)2 (1), we could compute (2) in O(k) for every i, using two arrays: one to store (1) and other to store prefix product of (1), which turns out to give us (2). This would lead us to a O(nk) solution that does not seem to fit into the TL.
(2) in O(k) for every i, using two arrays: one to store (1) and other to store prefix product of (1), which turns out to give us (2). This would lead us to a O(nk) solution that does not seem to fit into the TL.
Further optimizing it, we can decompose terms in such way that we need to compute i2k - 1 only for prime i:
We can use a sieve and compute i2k - 1 for each prime in O(k). For composite numbers we can just multiply what we have just computed for it's prime factors. We will have something like O((n + k)logn).
Как решать вторую задачу из Div2?
Систесты еще не кончились, но вроде это правда:
Построим орграф с ребрами i->a[i] и запустим топологическую сортировку. То, что получим — и есть оптимальная перестановка. Почему это так? У нас есть 2 типа компонент связности: бамбук с петлей на конце и большой цикл. Бамбук правильно отсортируется ибо петля ни на что не влияет. Цикл отсортируется правильно, потому что вне зависимости от начальной вершины ответ всегда "количество вершин в цикле" — 1.
P.S. Пока писал — зашло
Можно ли решить полным перебором?
Смотря каким.
У меня с ходу ничего кроме O(n!) в голову не пришло, но 50! — это нереально много
Am I the only one who is annoyed by the way authors are choosing the bounds? It seemed to me that the author was aiming for O(n^4) complexity, and O(k*n^4) should TLE. Nope, TC is fast enough to make that pass too. Why didn't the author make k equal to a 100? In that case the difference would be clear. Very weird choice IMHO, and a spoiled challenge phase for many participants ...
i actually did O(n ^ 4 + (k^3)n^2)
My solution runs in O(mnk3), which will be too slow with k = 100 :P
Well, there are n^2 k + k^5 solutions, so if anything should be increased is n
That would be OK too ...
Agreed. I wrote O(k*n^4), but it was 2.5 locally, so I spent some time to rewrite a O(n^4) (actually O(n^2(n^2+k^2)). Didn't know that TC servers are so fast.
There were solutions with O(n^2 k^2) though I didn't see anyone passed with such solution.
Really? How? The best I've come up with so far is O(n^2 k^2 log(n+k)).
If your idea involves keeping some sort of priority_queue and only altering k ^ 2 elements at a time (which is what I've done), I think you can just keep a sorted array and iterate at most k ^ 2 steps away from the max value each time.
That works, but it's O(n^2(k^2+log(n)), so it's not what we're looking for if n>>k.
EDIT: We can use the fact that each cell's value is O(poly(n)), so we can radix-sort in linear time, making it O(n^2 k^2). I have a feeling that's not what AU.Bahosain meant though.
Hmm, indeed. What about:
You only need the top k ^ 2 + 1 elements in the array. You can avoid sorting it by partitioning it with a linear time order statistic.
The logn comes from sorting the cost of all cells outside the loop.
I know, that's why I was suggesting that we drop the sorting and partition the cells instead.
Ah, and that's the solution. Thanks.
"I didn't see anyone passed with such solution ."
Oh. I thought you meant they coincidentally had minor typos, but the ideas make sense. But you inspired someone to find such a solution anyway, scroll up.
Mine was O(n^2 (k^3 + k ^ 2 log(k ^ 2))) and it passed. I was actually testing for K = 100 and it was running in 9 seconds locally but I decided to submit anyway. Only during the challenge phase I noticed that K was at most 10.
It can be also solved with a lot of other possible complexities. For a different brute working in N^2+K^5 (something like "check K^2+1 best cells") K=100 will be too much :)
Looking at standings, this problem was already too hard for div1 250, with higher constraints it will be an overkill.
Spoiled challenge phase? In which way?.. If you don't have an idea how many operations can be performed within 2 seconds — that's not fault of TC. If you are not sure about such solution — write it during intermission and run on maxtest. Sounds like an obvious part of preparation for challenge phase.
I checked my solution both at CF (honestly I simply forgot that I can run custom test at TC) and later at TC to make sure that it works fast enough. It works in 0.7 without any break's etc., so probably constraints are not too strict for naive solution.
And while I don't like this problem in general, yet I think that it will be a good lesson to people who think that 1 second is equal to 10^7 operations.
Upd. I see a lot of messages about naive solutions getting TL; it is a bit surprisingly for me. Maybe I am wrong about constrants being not too strict. Still we have n^4*k/2 here, which is 5*10^8 pretty simple operations. I used to believe it should pass without any problems.
Well, if there's time to write a dumb solution then it's the best way. I resubmitted this problem, because my original solution was too slow (I ran it on TC and it got TLE), so I rewrote it and was under impression that other solutions can TLE as well.
10^9 additions are OK, 10^9 array accesses are on the edge.
My complaint is that ideally authors should avoid putting bounds that are on the edge. For example, if n is 5*10^5, everyone will understand that n^2 is too slow. The only exception to this rule is when author is trying to hide greedy approach for the solution or something.
P.S. Did someone get n^4*k AC with Java?
My n^4 * k in Java didn't pass. Maybe I could have optimized a bit. But I think it's not nice that n^4 * k^2 in C++ can pass while most n^4 * k can't pass in Java. The constraints should be set so that solutions of the same complexity pass (at least regarding C++ and Java).
rng_58 mentioned below that they didn't notice that solutions with complexity O(n ^ 4 k) could pass. And maybe the problem author tested his solution in Java. It's pretty rare that the expected solution doesn't run in time for Java in TC.
Yes, the author's solution must always be in Java. It's hardwired in the problem submission applet (MPSQAS).
I think that any solution that is intended to pass should do that in 2x(and for TC its even more because of lack of pre-testing).
And 10^9 is clearly near the boundary.
It is a common opinion that constant optimization is bad and evil and should never be required in a contest. In an ideal world, CPUs could do 10^1000 operations per second, and we would set n=10^400, and it would be clear that asymptotics are everything.
The complaint here is that it would be possible (and easy) to make sure that constant optimization doesn't matter. If you want n^4k^2 to pass, set n=40: it passes easily and you still don't have any unintended brute force passing. If you don't want it to pass, set n=500, and the intended n^2k^2log(n) still passes easily. But with the current n=100, some n^4k^2 implementations pass and some fail, and many of them are very close to the border, making it near impossible to figure out whether a challenge is needed.
I solved 250 without any thinking. I don't really like it, either.
Just bruteforce all costs for all possible (i, j), sort them by decreasing cost, try all placements of (i1, j1) for base 1 in this order, for each of them all placements (i2, j2) of base 2 with smaller cost in this order. Bruteforce the cost of their intersection. If it's 0, break the inner loop (nothing better to find).
It should run decently fast, something like O(N2K4) worst case, with obvious optimisations like precomputing the intersection cells for all interesting values of (i2 - i1, j2 - j1).
Yes, sorry, we completely agree with you. We didn't notice that O(n^4 * k) is so small.
I did a O(k * n4) brute force solution that tried all possible pairs for each station, but counting each pair only once (second station must be to the right or lower than first station) and it passed system tests with the slower test case working in barely over 1 second, so the time limit was pretty comfortable for the given constraints.
No.. the time limit was not "pretty comfortable" . Thinking that naive brute force solution of O(n^4*k) would definitely time out, many people including me coded a better algorithm in terms of complexity (e.g. i did O(n^2*k^2*log(n))) which obviously took me much more time to code.
n4 * k for the current values of n and k is 1000M operations, which at first glance should time out for 2 seconds. But if you give it a better analysis, you'll see why it passes.
Upd: I was wrong, couldn't find break with some sorted sequence.
Никто не спрашивает почему-то: как решать div.2 Hard?
Huh, does anyone have any idea how to solve hard? Burnside lemma obviously needs to be applied and group generated by those operations described is group of permutations, but counting those stabilizers seems to be very hard problem. Maybe we can start by asking ourselves about an easier problem — we are given a permutation — how to compute size of its stabilizer?
Hint: construct a graph with n vertices, and if the i-th element is j, add a directed edge from vertex i to vertex j.
Did you mean ith element of permutation or ith element of a particular array from S? Am I right that Burnside's lemma needs to be applied? I already considered how permutation decomposes into cycles, but it seems hard to get a good grisp of which arrays remain unchanged under an action of a fixed permutation. If I'm not mistaken then if we have a cycle of length l then on corresponding positions in array we should put elements from a cycle of length d such that d divides l. But that constraint on k makes everything much harder and we are not allowed to count permutations one by one, so...
The symmetric group acts like conjugation (prove this!). Think about what the conjugation classes are for k=1 (you have probably seen this before) and prove that it's the same idea for every k. Then it should be obvious how to count the classes.
Could you please give a general idea of you solutions for Div1 250? The complexities that you are mentioning seem to vary a lot.
Could anyone tell what were possible approaches to hacking 250? There were very many hacked solutions, but I don't feel like going through all those tons of different long and ugly codes. I also don't believe that most of hacks were caused by TLE since as already established here, TC servers are so fast that even most naive bruteforce O(n4k) could pass (I tried hacking O(n4), but of course my attempt was unsuccessful).
Btw, what the hell is wrong with CF LaTeX — "n^4 k" shows as if it would be n^{4k} x_0??
a = 000000,109901 x = 0,0,0 y = 0,1,2
For those who had a greedy solution (trying to choose the maximum station first).
I hacked for WA, most of them add the value of cell two times, the correct answer is 55
Samples are well-picked, as usual :)
At first glance it seems that simply picking two best cells and prinintg sum of their scores (without even taking care about cells counted twice) passes them. Am I right? :)
Picking best cell and then best cell among remaining ones definitely passes samples, and I saw a few such solutions.
Some people submitted O(N4 * K2). Some people submitted it with some heuristics :)
Lot of people simply had bugs. As I said, it seems that you may pass samples without even taking care about cells counted twice.
P.S. And I believe that O(N4k) will not work within 2 seconds :)
I hacked a solution which always considered n == m.
Was it passing at least samples :d?
Yes as all examples except last one had n==m. And in the last example the answer was 0 :)
What's more — that solution also passed 2 TLE challenges as the provided input was n == m == 100.
Unfortunately it passed samples. I had FOR(i,0,n) FOR(j,0,n) istead of FOR(i,0,n) FOR(j,0,m) ... One letter from AC :/
Shit happens :/
my code had the same error, but i luckily spotted it just before submitting :P
O(n^2 m^2 k) solutions of 250div1 passed , that's fine. but how O(n^2 m^2 k^2) can pass ? look at wzw921026's submission in room 22 or in division summary (I couldn't copy his code)
Can some one please tell me what's wrong with This Solution(Div2 Hard), I am getting Wrong Answer for large tests.
We had to calculate i^(2^k -1) for all i 1 to n and range of k was 1 to 400 and we had to take mod of it and its range was 1 to 10^9.
What we can do is multiply i^(2^k-1) with i and divide by i. So it becomes i^(2^k)/i. Now we need to solve this.
We can solve the numerator as follows.
Let us first multiply mod with i so it becomes mod = mod*i. I have done this so that I can just divide the final result with i. It will be clear in a moment.
Now lets run a loop for i 1 to n.
for i 1 to n: res += calc(n,k,m) where n,k are the same as given in problem statement and m is m*i res /= i res %= m
Now for the calc function.
calc(n,k,m): for i 1 to k: ret *= ret // this will be (i^2)^k ret %= m return ret
This will be done in time complexity of n*k which will be 4*10^8 in the worst case. Which should pass.
Yeah I got it, Thank you.
I saw a solution for Div2 Hard which computed Euler Totient Function of m and then used it to find (2^k)%phi(m). What is the approach behind this?
It's consequence of Euler's theorem but I think it's not applicable in this problem because gcd(a, n) ≠ 1 might be true for some testcase. I don't know if, for this problem, there's a simple trick to deal with this particular case, but I guess that's why we had so many hacks.
Can some one explain me div2 medium answer. I am not able to come up with a solution.
[Div 2 — hard] Can somebody help me find wrong of my code. I've used Euler's phi function. I've use the formula: a^b % c = a^(b % phi(c)) % c. http://ideone.com/V31FsJ
I think when gcd(a, n) = 1, what's clearly not the case.
when gcd(a, n) = 1, what's clearly not the case.
What was the solution to div2 500?