Codeforces Round #306 (Div. 2) Editorial

#	User	Rating
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

#	User	Contrib.
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

550A - Two Substrings

There are many ways to solve this problem. Author solution does the following: check if substring "AB" goes before "BA", and then vice versa, if "BA" goes before "AB".

You can do it in the following way: find the first occurence of "AB" then check all substrings of length two to the right of it to check if substring "BA" also exists. Then do it vice versa.

Complexity of the solution is O(n), where n is the length of the given string.

550B - Preparing Olympiad

Because of the low constraints, this problem can be solved by complete search over all problem sets (there are 2ⁿ of them).

For every potential problem set (which can be conviniently expressed as bit mask) we need to check if it satisfies all needed criteria. We can simply find the sum of problem complexities and also the difference between the most difficult and the easiest problems in linear time, iterating over the problems that we included in our current set/bitmask. If this problem set can be used, we increase the answer by one.

Complexity of this solution is O(2ⁿ·n).

550C - Divisibility by Eight

This problem can be solved with at least two different approaches.

The first one is based on the "school" property of the divisibility by eight — number can be divided by eight if and only if its last three digits form a number that can be divided by eight. Thus, it is enough to test only numbers that can be obtained from the original one by crossing out and that contain at most three digits (so we check only all one-digit, two-digit and three-digit numbers). This can be done in O(len³) with three nested loops (here len is the length of the original number).

Second approach uses dynamic programming. Let's calculate dp[i][j], 1 ≤ i ≤ n, 0 ≤ j < 8. The value of dp is true if we can cross out some digits from the prefix of length i such that the remaining number gives j modulo eight, and false otherwise.

This dp can be calculated in the following way: let a_i be ith digit of the given number. Then dp[i][a_imod8] = true (just this number). For all 0 ≤ j < 8 such that dp[i - 1][j] = true, dp[i][(j * 10 + a_i)mod8] = true (we add current digit to some previous result), dp[i][j] = true (we cross out current digit).

Answer is "YES" if dp[i][0] = true for some position i. For restoring the answer we need to keep additional array prev[i][j], which will say from where current value was calculated. Complexity of such solution is O(8·len) = O(len) (again len is the length of the original number).

Code for DP solution:

Spoiler

#include <bits/stdc++.h>
 
using namespace std;
 
#define sz(x) (int) x.size()
#define all(a) a.begin(), a.end()
#define prev sadasdjksgjkasjdklaj
 
const int MAXN = 105;
 
string s;
int n;
bool dp[MAXN][8];
int prev[MAXN][8];
 
int main() {
 
    getline(cin, s);
    n = sz(s);
 
    memset(prev, -1, sizeof(prev));
 
    dp[0][(s[0] - '0') % 8] = true;
 
    for (int i = 1; i < n; i++) {
        dp[i][(s[i] - '0') % 8] = true;
 
        for (int j = 0; j < 8; j++) {
            if (dp[i - 1][j]) {
                dp[i][(j * 10 + s[i] - '0') % 8] = true;
                prev[i][(j * 10 + s[i] - '0') % 8] = j;
 
                dp[i][j] = true;
                prev[i][j] = j;
            }
        }
    }
 
    for (int i = 0; i < n; i++) {
        if (dp[i][0]) {
            string ans = "";
            int curI = i, curJ = 0;
 
            while (true) {
                if (prev[curI][curJ] == -1 || prev[curI][curJ] != curJ) {
                    ans.append(1, s[curI]);
                }
 
                if (prev[curI][curJ] == -1) break;
 
                curJ = prev[curI][curJ];
                curI--;
            }
 
            puts("YES");
            reverse(all(ans));
            cout << ans << endl;
            return 0;
        }
    }
 
    puts("NO");
 
    return 0;
}

550D - Regular Bridge

Let's prove that there is no solution for even k.

Suppose our graph contains some bridges, k = 2s (even), all degrees are k. Then there always exists strongly connected component that is connected to other part of the graph with exactly one bridge.

Consider this component. Let's remove bridge that connects it to the remaining graph. Then it has one vertex with degree k - 1 = 2s - 1 and some vertices with degrees k = 2s. But then the graph consisting of this component will contain only one vertex with odd degree, which is impossible by Handshaking Lemma.

Let's construct the answer for odd k. Let k = 2s - 1.

For k = 1 graph consisting of two nodes connected by edge works.

For k ≥ 3 let's construct graph with 2k + 4 nodes. Let it consist of two strongly connected components connected by bridge. Enumerate nodes of first component from 1 to k + 2, second component will be the same as the first one.

Let vertex 1 be connected to the second component by bridge. Also connect it with k - 1 edges to vertices 2, 3, ..., k. Connect vertices 2, 3, ..., k to each other (add all possible edges between them), and then remove edges between every neighbouring pair, for example edges 2 - 3, 4 - 5, ..., (k - 1) - k.

Then we connect vertices 2, 3, ..., k with vertices k + 1 and k + 2. And finally add an edge between nodes k + 1 and k + 2.

Build the second component in the similar manner, and add a bridge between components. Constructed graph has one bridge, all degrees of k and consists of O(k) nodes and O(k²) edges.

Complexity of the solution — O(k²).

550E - Brackets in Implications

Let input consists of 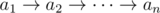$\text{[math]}$ , a_i is 0 or 1 for all i.

Let's show that there is no solution in only two cases:

1) a_n = 1.

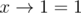$\text{[math]}$ , for all x, and no parentheses can change last 1 to 0.

2) Input has the form $\text{[math]}$ or its suffix with at least two arguments.

This can be proven by induction. For input $\text{[math]}$ there is no solution, for longer inputs any attempt to put parentheses will decrease the number of 1s in the beginning by one, or will introduce 1 in the last position (which will lead to case one).

Let's construct solution for all other cases.

1) For input 0 we don't need to do anything.

2) For input of the form 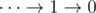$\text{[math]}$ we don't need any parentheses, the value of this expression is always

3) Expression in the form $\text{[math]}$ (where second missed part consists of ones only). Then $\text{[math]}$ .

Complexity of the solution is O(n).

dp[i][a[i]] = 1; prev[i][a[i]] = -1; if (dp[i - 1][j] == 1 && dp[i][(j * 10 + a[i]) % 8] == 0){ dp[i][(j * 10 + a[i]) % 8] = 1; prev[i][(j * 10 + a[i]) % 8] = j; } if (dp[i - 1][j] == 1 && dp[i][j] == 0){ dp[i][j] = 1; prev[i][j] = j; }

void recursive_print(int i, int j){ if (prev[i][j] == -1){ cout << a[i]; return; } int k = prev[i][j]; recursive_print(i - 1, k); if ((k * 10 + a[i]) % 8 == j){ cout << a[i]; } }

Create a bridge. Than create (k — 1), K(k, k) (complete bipartite graphs). Remove 1 edge from each (k — 1) bipartite graphs. Connect nodes of removed edges of (k — 1) / 2 bipartite graphs to the one endpoint of the bridge and of other (k — 1) / 2 bipartite graphs to the other end of the bridge.
So, total nodes = (2 * k * (k — 1) + 2), total edges = (k * k * (k — 1) + k).

Create K(k + 1) out of vertices 1..K + 1, remove (K - 1) / 2 edges, where all vertices chosen are different. Connect these k - 1 distinct vertices to the bridge vertex 2*k + 3. Connect 2*K + 3 to 2*k + 4. Now construct K(k + 1) out of vertices K + 1 .. 2*K + 2, and proceed similarly.

for(i=1;i<n;i++) { for(j=0;j<8;j++) { dp[i][d(i)%8]=1; store[i][d(i)%8]=s[i]; //Added the above two lines instead if(dp[i-1][j]) { store[i][j]=store[i-1][j]; store[i][(j*10+d(i))%8]=store[i-1][j]+s[i]; } dp[i][j]|=dp[i-1][j]; dp[i][(j*10+d(i))%8]|=dp[i-1][j]; } }

Comments (100)

Show archived | Write comment?

monkey.coder

9 years ago, # |

+17

please correct the format of problem C editorial,, it seems print the date

→ Reply

ADJA

9 years ago, # ^ |

Thank you!

homealone1

Problem C is very easy. Don't need Dp

yes, it has explained in this editorial

Oh. yes. I'm sorry :D

sampriti

Can someone tell me why my A got TLE? : http://codeforces.net/contest/550/submission/11420305

I used Regexp in Ruby.

nanobyte

https://swtch.com/~rsc/regexp/regexp1.html. I think Regexp has a exponential running time as mentioned in this post. Also from the post :- "Perl, PCRE, Python, and Ruby are all using recursive backtracking". Hope it helps.

P_Nyagolov

← Rev. 2 →

Do you mean bi-connected component by strongly connected component? If not, what is a strongly connected component in an undirected graph, I tried to google it and found nothing :)

thethong.ngu

Me too, I don't understand why there is a strongly connected component in undirected graph.

blue__legend

7 years ago, # ^ |

no bi connected components are different . Suppose you have a undirected tree then it is strongly connected but not biconnected. Biconnected components means there are always atleast two edge disjoint path between any pair of vertices in the component. It means there is no bridge in that component.

Good to know about biconnected. So what does strongly connected mean?

shervin

in the bottom of the explanation for C there is a O(8·len). but i think that in the big O notation you shouldn't write constants.

Timur_Sitdikov

Yes, you are right. It's written in such a way to show that if you have the same problem with some d instead of 8, you can solve it in O(d·len).

ShalinShah28

Hey!

For problem C, can you please explain the method to restore the answer using prev[i][j] in its DP solution?

You should calculate it when you are finding DP: for example,

When you are printing answer, you may do it recursively, like

Thank you for your reply. I have one more confusion though.

When we cross out the 'i'th digit (i.e when we do not consider it), why is the DP equation : dp[i][(j * 10) % 8] ?

I mean, why are we doing (j*10)%8 ? Why not just leave it as it is, because we are crossing out the ith digit?

Should it not be like below.?

if (dp[i — 1][j] == 1 && dp[i][j] == 0){ dp[i][j] = 1; }

Yes, you are right, it should be j instead of j mod 10 in dp and prev. Thanks!

NGUYEN_THANH_LOI

6 years ago, # ^ |

Excuse me, could you explain to me the first if? :

if (dp[i - 1][j] == 1 && dp[i][(j * 10 + a[i]) % 8] == 0) {}

How can we calculate

dp[i][(j * 10 + a[i]) % 8]

when we know

dp[i - 1][j] ?

I really don't understand although read editorial 3 times.

Thank you very much indeed.

_dp95

5 years ago, # ^ |

dp[i][j] states if it's possible to achieve the remainder j by using upto i numbers. So, if we include the a[i], the new remainder can be calculated as (j*10 + a[i])%8. You can read the editorial of 490C - Hacking Cypher which uses the similar approach in calculating remainder.

Hd7

Hello anh NGUYEN_THANH_LOI =)) Up to now, have you understand that? :v

=)) Who are you?

Your recursive_print(i,j) function is so clever. But i think your code has a bit trouble. Timur_Sitdikov For the cases, you take the number a[i] but it doesn't change the module 8, you must set prev[i][mod] = mod, so your recursive_print will work well.

if (dp[i-1][j] == 1) {
    dp[i][(10*j+a[i])%8] = 1;
    prev[i][(10*j+a[i])%8] = j;
    dp[i][j] = 1;
    prev[i][j] = j;
}

Isn't it written in my listing on lines below (from 7th to 10th)?

if (dp[i - 1][j] == 1 && dp[i][j]  == 0){
    dp[i][j] = 1;
    prev[i][j] = j;
}

Or I misunderstood you?

Thank you, i don't miss your code (from 7th to 10th). Your code takes at least at possible digits to catch the goal, and i think by the way at most at possible, so only if dp[i-1][j] == 1, not even dp[i][(10*j+a[i]] != 0, i take the a[i] digit. Thanks to your reply, I understand completely your ideal. Thanks a lot!

stargazer

Actually O(8*len) = O(len). It's not necessary to write the constant, but you can.

Seems Codeforces has new feature: autocomment about post changes. Please ignore this comment.

Zlobober

+31

The idea was not to edit such auto-comments so that everybody ignore them =) I guess we'll remove the option of editing auto-comments.

mohamed.mehany

+15

In problem C, I think the first approach can be better than O(len^3), O(125*len) can bee achieved, check 11430246

ggok

hey can someone explain how people solved B without using recursion ?

achaitanyasai

You can solve it by Bitmasking. You can Refer [my solution].(http://codeforces.net/contest/550/submission/11425633)

Aviously

Here is my solution (it doesn't use recursion): 11424247

Each set of problems corresponds to a binary number. For example, if we had 5 problems total, then the number 10101 would represent a set containing problems 1, 3, and 5.

Because of this, we can just count from 0 to 2ⁿ in binary and test every possible subset.

Use the first n bits of an int mask to represent a subset. If the i-th bit is on, then it means the i-th element is in the the subset. Just iterate the mask from 1 to 2^n — 1.

prateek_jhunjhunwala

Read this tutorial on how to find the power set of a set. POWER SET

Farhod

http://codeforces.net/contest/550/submission/11421622

TomBombadil

In problem D, how did you come up with the magic figure of 2k+4?? Can you provide any intuition for that?

← Rev. 3 →

Actually it is the minimum needed number of nodes (we thought about requiring it, but agreed it would be too hard).

I or Timur will post the proof later, if you want it and won't come up with it yourself :)

Please post explanation if possible.

Hi. Actually I just noticed that this proof is available in the Russian version of editorial :)

Here is the translation:

For k ≥ 3 let's find minimum number of nodes needed. The graph will contain at least one bridge and at least two strongly connected components, that are connected with other part of the graph with exactly one bridge. Each of these components will contain at least k + 2 nodes (one node that is connected to the bridge is connected with k - 1 edges with other nodes in the component. Other nodes in the component will have degree k — odd number, so the total number of them should be even, to make component right graph by its own [see handshaking lemma]. So this min number of other nodes is k + 1. Therefore total number of nodes in the component is minimum k + 2 ---- one incident to bridge, k + 1 not incident).

There are at least two components with at least k + 2 nodes in each, so minimum is 2k + 4.

Prime21

When we want find a bridge side in th graph . so we can think of two grpah has only one vertex's degree is k-1 ,other's degree is k. And then we connect the graph and another.If we want to get the grpah which has only one vertex's degree is k-1 ,k+2 vertexs can get the graph.... And maybe solving other constructive algorithms can help you.

i didnt, i went for 4*k-2. its pretty easy actually. first consider the bridge and name the vertices u and v. then add k-1 other vertices to the right side and connect all of them to v and them add another k-1 vertices to the right side and connect all of them to the previous k-1 nodes so now those k-1 nodes + v have degree k but the new vertices have all degree k-1 since k is odd then k-1 is even and you can connect every two adjacent pairs of the new k-1 vertices to each other so they now all have the degree k and now do the same thing for u and you are done.

Beresta

For me its more like 2 * (k + 1) + 2, which is equal to his formula.

To get weight k in one component we need exactly k + 1 nodes. We have two components, so its 2 * (k + 1). Also we have a bridge, which is 2 more.

Shouldn't the degree of EVERY node be equal to k? The degree of the (k+1) nodes in each component is k, but what is the degree of the 2 nodes which form the bridge? Isn't it just one?

Yes it should. And it would :)

My algorithm: Generate graph of k + 1 nodes, each connected to each. Remove k-1 edges from there and connect these nodes to the bridge one. After that, you'll have k+1 nodes with k degree, and bridge node with k-1 degree. Duplicate this graph, so you get two of them. Connect bridge nodes. Solved.

UPD: Forget to tell, that we should pick edges for removing carefully — each of them should have unique nodes connected, so no duplicated allowed (because if any dup k-degreee would be violated)

amangoeliitb

The solution for E is not clear to me Please help if possible

TsunamiNoLetGo

You must be clear fist on the fact that (x->1 = 1)

This means that the last number in the input must be zero.

So now our sequence takes the form "xxxxxx...0"

Now we want to make the second to last number equal to 1 in order to have (1->0 = 0)

Now we have two cases:

Case 1 "xxxxxx..10"

You can just leave the sequence as it is ... all the numbers to the left of the 1 will just have no effect .. and then the final value will be (1->0 = 0)

Case 2 "xxxxxx..00"

We need to turn this new 0 into a 1 somehow in order to be like case 1.

In order to get rid of this zero we have to match it with some other number.

From the rules, we have (1->0 = 0) and (0->0 = 1), so obviously we will try to match this 0 with another 0.

So we will search for the first 0 to the left of this 0.

So our sequence now takes the form "xxxx...0111..1100"

We can get rid of this group of 1s by grouping (1->1->1->1->....->0 = 0)

So now our sequence takes the form "xxxx...0(111..110)0" = "xxxx...000"

Now you will just have to group these two 0s together to change them into 1

"xxxx...(0(111..110))0" = "xxxx...(00)0" = "xxxx...10" = "0"

deer

Great explanation , i just wish codeforces editorials were written like this .

vsanjay_nitdgp

awsome explaination....thnks a lot.

ashish1610

I was unable to complete my code of D during the round. I did it differently and it was more intuitive.

My submission : Code

kshitij_jain

Could have done better by creating just 2 such bipartite graphs and removing (k - 1) / 2 edges from each one of them.

I suppose you meant edges not nodes.

Yes, sorry for the typo.

AmbarPal

Could have done even better by taking a completeGraph(k)[or K(k)]. Refer: http://codeforces.net/contest/550/submission/11437241

EDIT: LOL, just realised the editorial does the exact same thing.

Adi6099

Problem B can be solved with partial sums?

Well, you can find all permutations of problems and test each segment of each permutation using prefix sum, but the complexity would be O(n!*n^2) and you would get a TLE. I don't know if we can do better than this (using partial sum, of course).

ana1nd_9

anyone did Problem B using recursion? I did using bit masking . Just curious !!

Darkmaster

I've solved it with recursion (Backtracking) 11423350

grayhathacker

In the recurrence of problem C,

I think when we are crossing out current digit,

recurrence should be:

dp[i][j] = max(dp[i][j], dp[i - 1][j])

Correct me If I am getting it wrong?

You're right. The editorial solution is appending a zero to j.

Skyshirk

Can you explain why need to append a zero to j? thx

There's no need for it. In fact, it's wrong as grayhathacker pointed out.

Kazim

+23

For problem D, if k is even, then Eulerian cycle exists, thus there are no bridges.

yaswanth

We can solve problem C in O(1000 * len) without using dp. First find all numbers which are less than 1000 and divisible by 8. Convert them into strings. Now check if any one of them is a subsequence of the given string. This can be done in O(len).

Seems wrong...

E.g. string: 214

The answer (YES, 24) is not a subsequence of the original string.

UPD: Or maybe you meant the solution like this one?

gautam94

24 is a subsequence of 214. Check the definition of subsequence here en.wikipedia.org/wiki/Subsequence

Yea, sorry, thought about it like "substring"

KhaledKEE

I think this would be 124 not 1000. Because there are only 124 numbers less than 1000 (Not including 1000) that are divisible by 8.

125

d_sqaure

18 months ago, # ^ |

Nice approach.But it is better to solve using dp.Using recursion+memoization it is solvable in O(2*8*length).

CMaster

E easier than D :)

I also think that E is easier than D but that is subjective. There are [to the date] 363 accepted solutions for E which is lower than half those for D (754 accepted solutions).

dkjsfkhg

I can't get what the editorial says about the dynamic solution for problem C. Can someone tell me how is it working with a c++ code?

richardzrc

can anyone provide dp solution for problem A? As dp was a tag in problem a

KayacanV

+11

almost 2000 user tag edit access... now it has "chinese remainder theorem" XD . can anyone provide chinese remainder theorem solution for problem A?

I almost used dp to solve it :P

11422078

haha cool enclosed is my dp solution http://paste.ubuntu.com/11587440/

Ares

In problem C I generated first 125 numbers which are divisible by 8, then convert each of them to string and find if any of them appears in the given string as a substring. This can be done in O(125*len)

rajat1603

so many brute questions , not sure is codeforces or bruteforces.

vovuh

I really liked D! Theoretical graph problem is much interesting than a algorithmic graph problem.

tdk93

Somebody should fix the tags for Div 2 Prob A. Seems like someone went crazy and added every possible tag to the problem.

vtcb

You could solve C in linear time ( O( (1000/8) * len ), actually ): just check for each multiple of 8 less than 1000 if it is subsequence of the input.

Seems that.But if n is large and mod is prime, that means is ok?

In Problem E, when I used the inbuilt 'string' in C++, I got a TLE at case:8. When I replaced the inbuilt 'string' with the character array char[], it got AC.

Here is my code using inbuilt string which got TLE : http://codeforces.net/contest/550/submission/11455328

Here is my code using character array which got AC : http://codeforces.net/contest/550/submission/11455369

Any reasons for that?

Nooor

Anyway, array of characters is a slightly faster than the string class - but it should not make sense and should not give an advantage to who uses array of characters instead -

but someone may use the string to produce a much slower running code inadvertently, How is it possible ?

Every appending operation uses + has a complexity O(n) where n equals to the length of the string,
- since C++ does a resize operation -
you may use the built-in push_back function instead or even initialize your string to have such a maximum length and append elements by a direct access using index . look here is your first submission, just swap + by push_back and got AC in 139 ms

StillANoob

550C- Which data type should I choose for the integer n <= 10^100 in C++? I am using long long, but with it test# 23 gives incorrect answer probably because of limit of long long.

SirNickolas

std::string will fit just well. :)

sandy999

I didn't get the idea behind the DP solution for the problem, "Divisibility by Eight." Could someone kindly explain the solution in greater detail?

kirakira

Let's first define DP state as dp( index , mod) = {0,1}, which means using the digits between the leftmost digit and digit at index, is it possible to make a number x such that x%8 == mod

We loop through all digit (i.e. loop through all index) for each digit, we have two choices naturally:

Ignore this digit (i.e. delete it)
Append this digit

For the first choice, dp( index , mod) |= dp( index -1, mod) for all mod

For the second choice, it becomes tricker.

Consider dp( index -1, mod ) for all mod

If it is true, then if we append current digit,

the modular at index will become ( mod *10 + digit( index ))%8

So we just update this way: dp( index , ( mod *10 + digit( index ))%8) |= dp( index -1, mod)

Here's my code using this idea: 12143232

wannabe_khiladi

Hey kirakira amazing explanation! But i would like to point out that even though your solution got accepted, the way you handled the dp table for filling the store table .. distorted the dp table filling base logic and even confused me in the beginning.

You just cannot assume dp[0][0]++

even though you have added store[0][0]=" " and further in the final ans checked

for(int i=0, l=strlen(s); i<l;i++) 
if(dp[i][0] && store[i][0].length())
{ cout << "YES" << endl << store[i][0] << endl;  return 0;}
    cout << "NO" << endl;

This way it distorts the dp table filling logic and even confused me in handling the base case. This can be managed just by adding

The rest is same .. this is my accepted solution 16596112 . Still better explanation than the editorial :) It helped me. Thank you!

nimom

7 years ago, # |

Please explain me the dp solution of problem C . thanks in advance :)

LionCaptial

dp[i][j] represents that is it possible to have the remainder j from 0 to i.

let me explain to you with the example

take the num 3454 for this number dp matrix will be of order 5*8

for i = 1 : only possible rem is 3

for i = 2 rem possible are: [3 for number 3] [2 for number 34]

in case 34 rem 2 is possible only you take numbers 3 and 4 both, right! so newRem = (rem*10 + a[i])%8 => (3*10 + 4)%8 === 2. To have the rem is equal to 2 you have to check whether it is possible to have rem as 3 which comes for previous i. That's where dp[i-1][rem] comes into play.

similarly, if you are not taking number 4 into account then rem == 3 which comes from prev number. So in this case too you have to check for dp[i-1][rem] is possible or not.

for i = 3 rem possible are: [3 for num 3] [4 for num 4] [5 for num 5] [2 for num 34] [5 for num 45] [7 for num 345]

You can observe that all the rem depends upon the prev values expect for the remainder of size 1 for that particular i that's why you take dp[i][a[i]%10] = 1.

I hope you understand the concept well!