We have two groups of nodes, group A consisting of N items, group B consisting of M items. There is an edge connecting node a of group A and node b of group B, where
a = i mod N
b = i mod M
where i is an integer.
Image description of the problem (http://codeforces.net/predownloaded/5a/b5/5ab5c142069cd987264c765383e682f622a7f0bf.png)
We need to find for each node if there is a path connecting to another node in the graph.
To create the adjacency matrix, I iterated from i from 0 to LCM(N,M) — 1, since after that, we would get same edge pairs. Now, discarding this approach, how can one find mathematically, if two nodes of the graph are connected by a path or not? This is actually my trimmed version of this problem (http://codeforces.net/problemset/problem/515/B)
The tutorial doesnot explain the GCD method to get O(N + M) complexity. I tried myself but couldnot go far. Any help regarding how it was derived will be immensely helpful.
If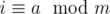
, and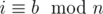 
, this implies 
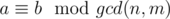So I found out that edge 'a' of group A can be connected to edge 'b' of group B if and and only if the remainder of nodes a and b are same when divided by the gcd. But, how to prove that this also works within the same group? Please help! I am trying to understand this problem, if any background theory is required you can list the topic and I will study it myself.