On April 4th, V (XVI) Volga Region Open Team Student Programming Contest was held in Samara State University.  And now, we invite everyone who haven't already participated in the championship to join the Codeforces training contest version on June 21st (11:00 — 16:00 MSK, UTC+3). We believe that participants of any level will find problems that will be interesting for them. The contest will probably be mostly interesting to participants with violet and orange levels (difficulty is 4 stars).
And now, we invite everyone who haven't already participated in the championship to join the Codeforces training contest version on June 21st (11:00 — 16:00 MSK, UTC+3). We believe that participants of any level will find problems that will be interesting for them. The contest will probably be mostly interesting to participants with violet and orange levels (difficulty is 4 stars).
This contest uses ACM ICPC rules.
Please, do not use the Internet, prewritten code and other sources: participants of the championship could not use any of these.
Contest was prepared by Dmitry Matov (Nerevar), Constantine Drozdov (I_love_natalia), Andrew Antipov (Sinner), Andrey Gaidel (Shlakoblock), Elena Rogacheva (elena), Sergei Shteiner (steiner), Alexander Efimov; Igor Baryshnikov (master_j) was of great help in English translation.











Isn't it a gym contest?
It's a gym contest.
Where can we find the link to the contest?
Contest will be available in Gym.
Great!!!! and thank's! :D
The registration is open now at gym :)
How to solve problem A? I saw a lot of AC on this, but I completely have no good idea on this one.
Minimum spanning tree, answer is maximum edge weight
Thanks you so much!
Let's build graph, where string are verticles abd between each pair of verticles there is an edge of weight equal to difference between strings. Now question is: what is the smallest K such a graph with edges with weights <=K is connected. It can be done using binary search. If we fix K we just do dfs which is going by edges <= K and check if graph is connected
my solution : build graph with recipes. g[i][j] is equal to distance between recipe i and recipe j. then use binsearh for answer: for the fixed answer there shuold be a path with all recipes and without edges with weight greater then anwer
How to solve K? I could not find any approach for this question but it has a lot of AC's so I am guessing it cannot be extremely hard.
After adding posA — posF which of the 2 things is considered processed?
Or do we consider both possibilities by dp somehow?
Letters 'A' and 'F', on positions posA and posF are considered processed at each step
I am sorry to keep on bothering you but could you please explain how your method works?
Just take a pen, write some examples and see that it really works. I don't have any other proofs.
Here's my idea: all we want to do is all As should come before F. Now considering A and F are some values such that A<F now we want to calculate no of inversions ( problem becomes similar to sorting an array with only operation of swapping two adjacent elements. I dont know proof but its equal to no of inversions in the array). Now main problem is every N can be taken as A or F. Which we can solve using a recursive function with two arguments 1.position we are referring to 2.no of Ns considered as F before this position. For every F just count no of As after that position. For every A dont do anything. Now for every N if we consider it as F do same thing as normal F and if its A then add to the answer total no of Fs before this position (original no of F + considered ones). I hope this helps.
Ah yes. This helps a lot.
I was already aware of the minimum swaps = inversion idea and during the contest was trying to reduce this problem into that one but was unsuccessful in doing so (because of the N's). Your solution takes care of that in a very nice manner.
Thank you.
Proof —
If we swap any two adjacent numbers, the number of inversions decrease by at most 1. So, we need at least inversions-count adjacent swaps to sort the array.
And as long as the array is not sorted, we can find two adjacent indices whose swapping will decrease the inversions. So, minimum number of swaps needed is indeed the number of inversions.
On a related note , what if the adjacent condition is lifted i.e. we can swap any two numbers, what is the minimum number of swaps needed ? If all the elements are distinct, we can solve by counting permutation cycles or by a greedy method. If there are equal numbers as well, i am not aware of solution. Does anyone know ?
I used brute force and greedy for this problem I fixed a position 'pos' and solve the minimun number of swaps when all 'A's are on the left of pos, even they can take pos, and every 'F' has to be on the right side.
That's when the greedy steps come....
Closest F to 'pos' on the left side will swap until it stays at 'pos', similar with closest 'A' to 'pos + 1' on the right side will swap until it stays at 'pos + 1', then swap what you have in pos and pos + 1. Do the same until you can't get one 'A' on the right side and one 'F' on the left side.
When there is no 'F' on the left side of pos or there is no 'A' on the right side of pos you'll have to swap 'A' or 'F' with 'N's to achieve the goal.
code : link My solution is O(n^3). I've simulated every step :/, it could be better maybe, without simulation...
nice and greediless :D
Can anyone explain how to solve G or provide a test case for which my submission 11697424 will fail?
Something similar to:
7 5
1 1 1 1 1 5 1
Correct answer is
7
+++++-+
but your answer is 5.
Correct approach is dynamic programming dp[i][j] — are we able to get number j after i moves.
Thank you.
Try this:
Any ideas for question I please??
Build pairs of < skill, field > for each course, sort all of them in increasing order by skill and find an interval [i, j] of courses which has the following properties:
Thank you!
I would add that you can find such interval in O(n) time using two pointers technique. Of course complexity of whole solution is still O(n log n) because of sorting.
very good problems with nice ideas , but is it necessary that statements be very inexpressive ??
How to solve F?
dp[i][a][b]— the best result foriprocessed indices,aof them are chosen for the first player,bof them — for the second player.There is also a flow solution but DP is much easier.
how is the flow solution modelled ? The DP was pretty easy!
a can be at most 400 and b can be at most 400 and i can be a most 400, a MLE will be given isn't it?
Thanks! I really enjoyed solving your problems! Specially "problem I" which was really interesting in my opinion!
Is it possible to discuss short write ups on the problems? Atleast on the ones with less than 50 AC.
Sorry for my bad English.
C) Main idea: go from up halls to downs and for each hall keep set of disjoint intervals. Interval is a structure with following parameters:
For each hall we can construct its intervals using intevals of previous hall (it is case when we come from up hall) and open segments of current hall (case when we start from that hall). After building intervals for current hall we have to merge them greedily. All that can be done in O(numberOfIntervals) operations if we keep intervals sorted by from and use two pointers. Maximum available value of numberOfIntervals is less or equal than , so we can process all halls with total asymptotic
, so we can process all halls with total asymptotic 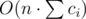 . Further we can find best interval. It is interval with minimal start such that to - start ≥ t. After we just need to restore the answer.
. Further we can find best interval. It is interval with minimal start such that to - start ≥ t. After we just need to restore the answer.
Source: pastebin.
D) I’ll just leave this here: part 5 in article.
E) Just find cutpoints and biconnected components and construct tree of biconnected components. After that we can use dfs on that tree to calculate for each cutpoint sizes of children components and size of parents components. English, Russian. It can be done in O(m) operations.
Source: pastebin.
H) It will be written later by me or elena.
J) In first calculate maxGame – prefix maximum of queries(lengths of games) and sort gamers by t. After that come from the last game to the first and for game number i will be add gamers with t ≥ maxGame[i] in DSU. Answer for game number i: g[i] * size(0), where size(0) — size of set, which contains knight. It also can be solved by BFS and TreeSet. Asymptotic: O(m·α(n)).
Source: DSU, BFS.
some write ups in rev 1.
Enjoyed problem H "A lot of work" a lot. Seems that most of the solutions are some kind of heavy-light decomposition which solves differently long and short colour chains. My solution is a bit different, at least in terms of the written code, there is no distinction between long and short chains, I solve both of them with the same code. The main idea is that the result function for a given colour chain is monotonous with regards to its forgetting parameter k, so if we know that f[k1] = f[k2], then we don't need to calculate the answer in between of k1 and k2. So for a given colour my solution goes as follows:
Submission: 11838173
Code
Your submission is not available for all.
Thanks, always forgetting that submissions in gym are not that easy to see. Plus this time they were submitted with coach mode enabled which makes them even more difficult to see.
And why will we use straightforward approach small amount of times?
Thanks for asking, I forgot to clarify that part. I claim that function f(k) will have no more than distinct values for all given values of k. The reason for that is that we can consider two cases:
distinct values for all given values of k. The reason for that is that we can consider two cases:
So we have distinct values in the result array. The entire point of the algorithm I described above is that it skips intervals where function doesn't change its value. So effectively it looks for all distinct values and then does binary search between adjacent different values to find the exact parameter value where the function changes its value. So in total it should be
distinct values in the result array. The entire point of the algorithm I described above is that it skips intervals where function doesn't change its value. So effectively it looks for all distinct values and then does binary search between adjacent different values to find the exact parameter value where the function changes its value. So in total it should be 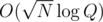 invocations of straightforward algorithm.
invocations of straightforward algorithm.
I think the idea behind heavy-light decomposition in this problem is similar to my intuition above but this solution uses this intuition only to prove its correctness while the code is simply does binary search + brute force approach which is very easy to code, that's why I wanted to share it.
Thanks;)
How to solve problem H by heavy light decomposition ?
Can someone give some tricky test case for problem E ? Thanks I'm not sure if I understand problem E correctly.