Today in one of our contests there was one difficult problem:
Define Rn is the sum of all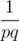 
such that:
p and q are positive integers, 1 ≤ p < q ≤ n
p and q are coprime. In other words, gcd(p, q) = 1
p + q ≥ n
Given the positive integer n (1 ≤ n ≤ 106), calculate R1 + R2 + ... + Rn.
I could not figure out any working solution. After the contest ended, someone mentioned a very interesting observation within his comment on the problem. That is, if we change the condition p + q ≥ n to p + q > n then Rn will always be 
(!). It was, indeed, a very obvious observation, but only on screen when we do a brute force run. I hoped for someone to come up with a mathematical explanation for it, but it seemed like no one got any ideas :D
How about you guys?
Well, think about what happens when you go from n to n + 1. On the one hand, you add pairs with q = n + 1, the sum of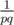
over those pairs is 
times sum of 
for p coprime with n + 1. On the other hand, you lose pairs with p + q = n + 1. For these pairs the condition gcd(p, q) = 1 is equivalent to gcd(p, n + 1) = gcd(q, n + 1) = 1. Also, for them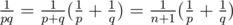 
. Because p < q, this is the same sum that we added.
That sounds perfectly logical! Thanks a lot! :D
Can you give the problem link? This problem is exactly same as this.