Hi everyone,I am learning Graphs for few days so every question looks graph to me.I tried this question and thought of graph(bfs) but for some reason it is running indefinitely.Any help appreciated :).Link solution
→ Pay attention
Before contest
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
25:00:50
Register now »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
25:00:50
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/22/2024 16:34:11 (i2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











It's not a graph problem, but a math problem rather.
Consider f(a, b):
Solve
=>
which then leads us to f(a, b % a)
f(a, b) = f(a, b % a) + b / a, if a < b
-
By the way, I like this problem. Thank you for pointing me to it :)
Hi :) Thanks for answer.Let me explain my approach to you,possibly you can tell what's wrong with it.I started with resistance one and everytime I add a resistance in parallel and add another in parallel(doing something like s*1/(s+1)(parallel) and (s+1) series) and like this I am extending bfs till I reach certain ratio which is provided in the question.My approach is very same like process in this question.Two buttons .How about my approach was that total rubbish ?
Your solution (the link you gave on the main post) doesn't check for collisions.
For example, you will visit both
1 + 1/2and1/2 + 1which shouldn't be necessary.Your solution is not rubbish. You are just relatively inexperienced :)
The state space is simply way too large.
Even if we're only concerned with integers, we're looking at a set with 1018 states {1, 2, ..., 1e18}.
Use induction on n.
Let us suppose we can say the minimum number of resistors that can give us (a/b).
Claim: We know the rational number when we try to increase the the resistors by 1 from a particular base rational number (a/b).
Since there are two ways to do this resulting in (a+b/b) and (a/(a+b)) by our induction hypothesis, we now know what the minimum number of resistors can be calculated from the answer of the base rationals number.
We conclude by saying that it is a minimum over two base rational numbers since in fact the resistor values can be arrived at in two ways.
f(a,b) = min. f(a-b, b), f(a,b-a) + 1 . a-b>=1 b-a>=1 wherever the case. f(1,x)=f(x,1)=x
But that is not fast enough due to constraints. We can however use the recurrence to find a better answer. Is there an efficient way to calculate f(a-b, b) faster ?
Maybe by using division algorithm a=b.q+r ?
Your conclusion is obviously correct, but far from sufficient to solve this problem.
How would you reduce the problem from a,b to something involving a,b,r,q where r and q are remainder and quotient?
Assuming you're asking the case with
a > bIt's rather straightforward.
Let me explain the intuitions. We have 2 equations: (1) R = Re + R0, (2)
 is greater than 1 and we decompose it into
is greater than 1 and we decompose it into 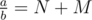 (where N >= 1 and M < 1), N has to come from equation (1).
(where N >= 1 and M < 1), N has to come from equation (1).
Notice equation (2) would yield results R < 1.
This means if
You said "f(a, b) = a / b + f(a % b, a), if a > b"
In that case f(5,2) = 2 + f(1, 5) = 2+5 = 7
I think it should be f(a,b) = a/b + f(a%b, b)
so that f(5,2) = 2 + f(1,2) = 2+2= 4
f(1,x) = f(x,1)=x
You're right. Made a typo there.
Thanks for pointing that out :)
Hey thankyou :)
You're welcome :)