Hello
I need Help please in this graph problem
I think you all know the minimum path cover problem in a DAG
You are given a DAG and you have to compose it into K paths so that every vertex must belong to exactly one path
So you have to find a solution where K is minimum
This can be solved by maximum matching.
But what if the vertex can belong to more than one path in the composition ???
For further understanding ... let's imagine this DAG
1->2
2->3
4->2
2->5
The standard covering will give us 3 as a result (1->2->3 , 4 , 5)
But in this version the answer would be 2 (1->2->3 , 4->2->5)
Does anyone have any idea?
Thanks in advance










Seems like if we consider a transitive closure of given graph (let's call it G), with its fixed non-disjoint path-covering, we can obtain a disjoint path-covering of a transitive closure of a given graph (denote it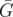 ).
).
Indeed, let's fix some not vertex-disjoint path covering of G. We can build almost "the same" path covering of the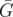 : add next path until the first intersection by vertex appears. Obviously, we can prevent this intersection by going through one of the "transitive-closure edges" (if needed, maybe there are some cases when we can simply stop at the vertex before the intersection). This procedure covers
: add next path until the first intersection by vertex appears. Obviously, we can prevent this intersection by going through one of the "transitive-closure edges" (if needed, maybe there are some cases when we can simply stop at the vertex before the intersection). This procedure covers 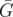 by exactly the same number of paths, but this time vertex-disjointly.
by exactly the same number of paths, but this time vertex-disjointly.
In similar manner we can prove a reverse statement.
In sum, if I'm not mistaken, you can just find a vertex-disjoint path-covering of transitive closure.
I'm not sure if I'm following you entirely, but if you're saying that the size of the minimal vertex-disjoint path-covering of a DAG is the same as the minimal vertex-disjoint path-covering of its transitive closure, then I'm afraid you're wrong. Consider V = {0, 1, 2, 3, 4} and E = {(0, 2), (1, 2), (2, 3), (2, 4)}. To cover G = (V, E) you need at least three paths, but you can cover its transitive closure with 2 paths.
That said, the general method to solve this problem still works, but you just need to forget about the transitive closure (just do the normal bipartite matching procedure on the graph itself, not its transitive closure).
EDIT: to expand on that for the OP: note that when we cover the DAG with vertex-disjoint paths, each vertex has at most one incoming edge, and at most one outgoing edge. The number of paths is thus equal to the number of vertices with no incoming edges (or equivalently, the number of vertices with no outgoing edges). How can we model this as a bipartite matching problem?
I see a way to cover G by two paths: (0,2,3), (1,2,4). Remember that we're not talking about vertex-disjoint case, paths can intersect.
Read again:
Vertex 2 belongs to two paths, thus the cover is invalid.
EDIT: Oh, nevermind, I can't read. Yea I guess you're right then, my bad.
This might help
So you just have to add edges from every vertex v to every vertex which is reachable from v, and then use the algorithm you described first.
Thanks all :) I appreciate it
I do have a simple algo put all the vertices in a set A (vertices are ordered by indegree) and do the following until set becomes empty.
This is very simple solution i am just checking what is the maximum number of nodes at a given level. and this is the answer.
It is just a simple idea using Topological sort technique.
Please verify it and give me feedback. if possible please provide me link as well.
http://www.lightoj.com/volume_showproblem.php?problem=1429 this is the problem
You have mentioned that the graph will be acyclic but this problem includes graph containing cycle even the second example in the sample contains two simple cycle. I think that we can modify my solution to find the answer.
actually i am not sure that your solution is right
becuase each vertex can belong to more than one level
anyway ... for this problem
find strongly connected components of the graph ... so they form a DAG and then continue
I'm trying to solve the same problem on LOJ and finding the transitive closure seems to be really the way to go ... but with V=1000 and E = 10000 ... finding transitive closure in O(V^3) using floyd or O(VE+V^2) using DFS seems to not be able to pass
is there a faster to find the transitive closure or is there a different approach that should be used ?
Pepe.Chess if you solved it ... how did you do it eventually ?