Всем доброго дня!
Я автор задачи С первого раунда Яндекс.Алгоритма и расскажу её решение.
Надеюсь задача вам понравилась. Сразу хочу извиниться, за то, что тесты были не достаточно сильными и квадратичное решение пользователя maksay проходит системные тесты. Когда состовлял простые решения для проверки тестов, забыл предусмотреть такой вариант решения, а случайные тесты с глубокими деревьями не смогли его отловить.
Итак, вспомним условие задачи. Дано корректное бинарное дерево поиска и набор ключей-запросов. Для каждого ключа-запроса рассматриваются пути, которые получаются, если поискать этот ключ в дереве и один раз в ходе поиска пойти не в ту вершину.
Сначала поймем, как решить задачу для одного ключа-запроса. Рассмотрим вершину в пути, после которой произошла ошибка. Предположим, что мы согласно ключу должны были пойти в левого сына, а пошли в правого. Это означает, что ключ-запрос лежит в интервале ключей левого поддерева, а мы перешли в правое поддерево. Отсюда сразу следует, что поиск этого ключа в правом поддереве приведет нас в вершину с наименьшим ключом. Аналогично, если мы должны были пойти в правое поддерево, а пошли в левое, то в левом поддереве мы придем к вершине с наибольшм ключом.
Посчитаем для каждого поддерева максимальный и минимальный ключи, которые в нем встречаются. Это можно сделать одним обходом в глубину. Теперь для заданного ключа-запроса несложно посчитать ответ задачи. Необходимо выполнить поиск этого ключа в дереве, и в ходе поиска смотреть на поддеревья, в которые мы пошли бы при одной ошибке, брать у них соответсвенно минимальный или максимальный ключ и накапливать ответ.
Теперь решим задачу для всех ключей-запросов. Для этого заметим, что ответ задачи для ключа-запроса зависит только от листа, в который мы попадем в ходе поиска по дереву. Поэтому, насчитаем ответ для всех листьев дерева одним обходом в глубину. После этого научимся для каждого ключа-запроса быстро определять в какой лист мы придем при его поиске в дереве. Для этого надо все ключи всех вершин дерева сложить в один отсортированный массив. Заметим, что в этом массиве будут чередоваться ключи листьев и внутренних вершин дерева. Бинарным поиском найдем пару вершин, между которыми лежит ключ-запрос, и выберем из этих двух вершин лист. Ответ для этого листа и будет ответом для данного ключа-запроса.
Таким образом, решение задачи требует двух обходов дерева в глубину и k бинарных поисков по массиву. То есть ассимптотика решения состовляет 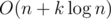 . Здесь n --- это количество вершин в дереве, а k --- это количество ключей-запросов.
. Здесь n --- это количество вершин в дереве, а k --- это количество ключей-запросов.
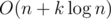 . Здесь n --- это количество вершин в дереве, а k --- это количество ключей-запросов.
. Здесь n --- это количество вершин в дереве, а k --- это количество ключей-запросов.










Определим бинпоиском в отсортированном массиве запросов, какие элементы пойдут в левое, а какие в правое поддерево корня. Запускаемся от поддеревьев и подмассивов рекурсивно, пока не дойдем до листьев.
`