Прошел первый этап XV Открытого Кубка по программированию. Как решать задачи А, Е, К?
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
6 дней
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
6 дней
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 25.11.2024 05:39:38 (j2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Авторы, пожалуйста, делайте сэмплы не на "отгребись", а для людей!
Цель сэмпла — в том, чтобы человек не мог сесть писать задачу с неправильным пониманием условия. Сэмпл в задаче I не демонстрирует ровным счётом НИЧЕГО. Пока мы не задали два клара, а Олег не прогнал их в авторском решении (их потом броадкастнули, кстати), понять, что называется одинаковыми подстроками, а что -- разными, было совершенно невозможно.
Ага, мы тоже задавали до бродкаста, нам ответили Read the problem statement.
Приведу переписку с жюри, так как это единственный приходящий мне в голову случай, когда жюри командного соревнования отвечает вопросом на вопрос :)
13 сен 2015, 13:20:56 Important Or Not? Distinct strings Does distinct in third type of message mean "distinct pairs (y, q) such that string (y, q) contains string (x, p) as a suffix" or "distinct substrings s of a string A such that s contains string (x, p) as a suffix" (in the other words, does distinct occurrences of a same substring counts several times)? 13 сен 2015, 13:36:28 Aren't (x,p) and the substring of A the same set? 13 сен 2015, 13:46:35 Important Or Not? No, they aren't :) For string "abacaba" pairs (2, 1) and (2, 5) represent both string "ab". Pairs (2, 1) and (2, 5) are distinct but substrings are the same. If the quries are: 1 2 1 (activate first "ab") 1 2 5 (activate second "ab") 3 1 1 2 (ask for substrings containing "b" as suffix) The answer is 2 (if two occurrences of "ab" count) or -1 (if not)? 13 сен 2015, 14:14:13 -1 13 сен 2015, 14:26:22 Important Or Not? Enabling one occurrence and disabling another If we activate one occurrence of a substring and deactivate another, is this substring still considered activated or not? Example: A = "abacaba" 1 2 1 (activate first "ab") 2 2 5 (deactivate second "ab") 3 1 1 1 (ask for substring containing "b" as suffix). The answer is 2 ("ab") or -1 (if "ab" is indeed deactivated by second query)? 13 сен 2015, 14:28:29 -1Как решать B и M?
M: возьмём и положим все полиномы в мультисет с компаратором, сравнивающим значение полинома A в точке xA и полинома B в точке xB (начинается всё из x = 1), а дальше будем составлять последовательность по условию задачи: забираем из мультисета полином с наименьшим значением и вычисляем, плюсуем его точечку и кладём обратно, и так ещё k - 1 раз.
В B я придумал какую-то глупость, не знаю, насколько она близка к реальности. Диагонали разного цвета не пересекаются, посчитаем количество клеток каждого цвета под боем, думая о диагоналях, как о строчках (/) и столбцах (\) в прямоугольной матрице, тогда количество клеток под боем можно посчитать по формуле включений-исключений: rows * n + columns * m - rows * columns. Из этого надо ещё вычесть «лишние» клетки, потому что диагонали на самом деле все разной длины.
И еще хотел узнать почему ответ gcd(n,k) в задачи G?
Пусть мы циклически сдвинули последовательность
1,2,3..nнаkвправо, тогда последовательность примет видk+1,k+2...n-1,n,1,2,3..kможно убедится что при каждом ходе в раунде мы переходим накклеток вправо циклически, так мы переходим пока не попадем на перевернутую карту, то есть можно подсчитать, что на каждом раунде убираетсяlcm(n,k)/kтогда нужно сыгратьn/(lcm(n,k)/k) = n*k/lcm(n,k) = gcd(n,k)раундов.A Let's compute answer for vertex v. We can visit an associative vertex u like this:
Firstly go some steps using given edges, after that go using reversed edges.
So Dfs(vertex, isReversed) will work perfect here.
From isReversed = false we can go to isReversed = true, but not in other way.
Code
K, dynamic programming and
meet in the middledivide and conquerSorry that I am in english.
Can you explain in more details problem K?
K dp(i, j) — first i keys are assigned, and we have covered first j alphabets.
dp(i, j) = min dp(i-1, k) + cost(k+1, j)
Let's denote optK(i, j) — optimal k that gives for us minimum.
We can prove that, optK(i, j) <= optK(i, j + 1)
let's calculate recursively calc(i, l..r, optKl, optKr).
Firstly, we can calculate dp(i, mid), then recursively solve for
calc(i, l..mid, optKl, opt(i, mid)) and calc(i, mid+1..r, opt(i,mid), optKr)).
321E - Ciel и гондолы also can be solved using this trick
Also, you can use convex hull optimization. Lets dp(i,j) — first i keys are assigned, and we have covered first j alphabets.
Code
K can be done by dp with a convex hull trick.
I would call it "divide and conquer" rather than "meet in the middle".
Indeed, thanks.
A: Конденсируем граф. Далее с помощью динамики по ориентированному ациклическому графу + битсетами определяем в каждой вершине битсет из её "потомков". Далее динамикой по развёрнутым рёбрам проталкиваем эти битсеты в потомков. Таким образом в битсете каждой вершины список потомков её предков, пройдёмся по ним и прибавим к ответу нужные числа. O(n2)
E: Из условий nk ≤ 105, k ≤ n следует, что k2 ≤ 105. Сортируем всех рабочих по опыту. Пишем динамику за nk2 вида dp[число рассмотренных рабочих][число взятых асистентов]["баланс" между асистентами и шефами ]. Баланс не должен становиться отрицательным.
Можно по-подробнее про А? Мы потратили немало времени на то, чтобы понять, как по набору множеств потомков за O(N^2) получить список пар, которые одновременно находятся хотя бы в одном множестве — не вышло, написали решение, которое описал Madiyar комментом выше.
Сначала мы находим для каждой вершины потомков. Потом, мы их "пропихиваем" вниз. В итоге в каждой вершине лежит список её "соседей". Пробегаемся по нему.
Ага, точно. Спасибо!
А: вы тут все извращенцы. Пустим из каждой вершины bfs по обратным рёбрам чтобы найти предков, теперь используем уже готовую очередь чтобы найти всех потомков этих предков. Либо dfs по парам (вершина, вверх/вниз). Из-за того что рёбер мало, сложность одного прохода O(N), по всем вершинам O(N2);
Зачем dfs по парам. dfs из многих вершин тоже можно запускать, просто used не надо чистить.
А , ну да :)
Вместо баланса можно хранить сколько пар уже взято, это более понятно :)
Мы решали А похожей идеей. Правда граф не конденсировали. Честно пускали дфс из каждой вершины, если в ней еще не были, и за дфс запихивали в битсет(назовем его Cur) все вершины, которые мы прошли в этом дфс. Пройдем по всем единичкам в битсете Cur и к битсетам(у нас для каждой вершины есть битсет вершин, с которыми эта вершина ассоциативна) всех вершин, в которых единички сделаем Or битсета Cur. Понятно, что если мы запустили из этой вершины дфс, из всех вершин, до которых мы добрались, запускать дфс бессмысленно, так как ответ останется таким же. Оценивать это решение не умею, может быть что-то около O(N^2)
Какое соответствие задач на украинской 1/8 и сегодня?
Как решать H, L?
H — будем считать ожидание времени до конца — величину D[components][v], где components — отсортированный вектор размеров компонент связности (таких всего 627, кстати), и мы стоим в вершине v. Формула пересчета — линейная, но внутри группы с одним components зависимости циклические, поэтому внутри группы будем считать Гауссом. А по components группы состояний образуют ациклический граф, поэтому получается решение а-ля динамика с Гауссом, которая работает за 627 запусков Гаусса.
А много кто знает как эту задачу решать за полином?
Я знаю другой способ, который полиномиальный и использует теорию случайных процессов. Можно понять, что мы фактически генерим случайную величину ξ, которая говорит, сколько нужно случайных ребер добавить в граф, чтобы он стал связным, а потом считаем сумму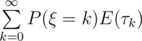 , где
, где 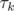 — первый момент, когда блуждая по графу, мы собрали k успехов (фактически, процесс восстановления некоторого случайного процесса). Распределение
— первый момент, когда блуждая по графу, мы собрали k успехов (фактически, процесс восстановления некоторого случайного процесса). Распределение  можно найти из уравнения восстановления, а распределение ξ как-то искалось аналитически (не помню, честно говоря, как).
можно найти из уравнения восстановления, а распределение ξ как-то искалось аналитически (не помню, честно говоря, как).
dp[edges][v]
Заметим, что все несвязные графы с одинаковым количеством рёбер равновероятны. Дальше всё как у Zlobober, для переходов мы предподсчитали кол-ва связных/несвязных графов с фиксированным кол-вом рёбер, а также суммарное количество мостов в связных графах при фиксированном количестве рёбер.
Предподсчёт за O(n6), гауссы за O(n5)
У меня очень похоже, а для чего нужно количество мостов?
Чтобы посчитать вероятность закончить игру прямо сейчас.
Если мы добавляем новое ребро в несвязный граф, и он становится связным, то это ребро было мостом. Верно и в обратную сторону. Поэтому мы считали кол-во переходов вообще и кол-во переходов, завершающих игру. Их отношение — это вероятность закончить игру сейчас.
Как решать I?
Построим суффиксное дерево. С помощью двоичных подъёмов можно для каждой строки определить вершину, в которую ведёт ребро, в середине которого мы бы оказались если бы искали её в суфф дереве как в боре. Давай в каждой вершине дерева хранить список длин "хороших" подстрок, которые кончаются в ребре, которое ведёт в неё. Выпишем вершины в порядке захода в них. Тогда когда к нам приходит запросов можно рассмотреть два случая:
Итого решение работает за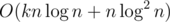 . При желании можно хитрыми махинациями переписать k-статистику за
. При желании можно хитрыми махинациями переписать k-статистику за 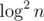 и решение станет не зависеть от k, то есть,
и решение станет не зависеть от k, то есть, 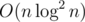 .
.
Код: #1zLpMn
P.S. Видимо, альтернативно можно решать суффиксным массивом. Для этого можно определять лексикографические границы заданной подстроки. Это всё ещё будет k-статистика на отрезке, однако это решение представляется мне громоздким и более сложным в реализации.
Umm can you please translate it into english? I could not quite get it by translator
Sorry for late answer.
Let's build suffix tree. After that with some kind of sparse table you can find the edge on which [l, r] substring lies in . After that let's in every node of suffix tree keep the set of strings which are important and lie on the edge that leads to this node. Also let's build segment tree on the nodes of suffix tree in the in-order of dfs, so any subtree of some node will be contiguous subsegment. At last, we can answer the queries. Let's consider two cases:
. After that let's in every node of suffix tree keep the set of strings which are important and lie on the edge that leads to this node. Also let's build segment tree on the nodes of suffix tree in the in-order of dfs, so any subtree of some node will be contiguous subsegment. At last, we can answer the queries. Let's consider two cases:
My code: #1zLpMn
Sorry for poor English :)
Thanks for the translation, I forgot to update that, I understood the solution looking at your code in previous post. I think you used Suffix Link tree of Suffix Automata, not Suffix Tree, right? Or are they equivalent (don't think so)?
Suffix link tree = suffix tree of reversed string
Идейно простое решение (немного не успели на контесте, но в дорешку зашло): возьмём все подстроки из запросов (а из запросов 3 типа — дополнительно подстроки + большой символ в конце), и тупо посортим (хешами, итоговая сортировка за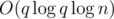 ).
).
Поверх посорченного массива сделаем дерево интервалов, которое умеет добавлять элемент за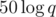 и считать k-ую статистику на отрезке за
и считать k-ую статистику на отрезке за 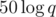 . Итого получается
. Итого получается 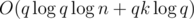 .
.
Как решать J?
Бин. поиск по ответу. Степени, которые > 4 очень быстро заканчиваются. Их быстро смерджим и в бин. поиске используем lower_bound. Для остальных, если они есть, можно посчитать число элементов оттуда, меньше середины отрезка в бин. поиске с помощью формулы включений-исключений.
Код: #aWIhkW
P.S. Теоретически должно заходить и когда мерджим последовательности с > 3, но на деле это получает TL. По крайней мере у меня.
Или можно ничего не мерджить, а посчитать количество членов искомой последовательности, которые не превосходят x. Для этого нужно воспользоваться формулой включения-исключения. Конечно, если ее считать напрямую, то это работает за экспоненту. Но степеней больше 60-ти для чисел, начиная с двойки, "не бывает" из-за ограничений задачи, а единичку вообще можно отдельно всегда посчитать. Для того, чтобы посчитать "правильные" коэффициенты для степеней от 1 до 60, нужно 1) считать их только для степеней, кратных хотя бы одной степени из инпута 2) рассмотреть их все по возрастанию, вычислить
coeffs[i]— сколько раз мы уже "посчитали" i-ю степень, и затем "добавить" ее с коэффициентом(1 - coeffs[i]). Вот код.Когда-нибудь чудо случится, и рандом в Яндекс.Контесте исчезнет. Не сегодня. Техника "пошли одно и то же решение 3-4 раза, если не проходит, и прогрей Яндекс" работает до сих пор.
Сабмитим на контесте
Сабмитим в дорешечку
Другая задачка без богомерзской джавы
Господа из ННГУ, которые сдают H до заморозки с плюса, КАК?
Я вот начиная с 3:00 полтора часа смотрел в AC-код и пытался понять, почему же он не работает на втором сэмпле. На клар нам ответили неправильно.
Вряд ли с этим что-то сделают, но осадочек неприятный.
Я тоже минут 40 смотрел. За это время успел посчитать на бумажке ответ, и он у меня сошелся с моим решением. Ну я забил и решил так отправить.
Мы тоже посчитали. Посабмитили минимум из всех вершин.
Ну изначально в условии про минимум вообще ничего не было сказано, так что я посчитал такую неточность менее вероятной.
Изначально в условии сказано "arbitrary" :)
Ну там есть слова типа "His goal is ...". Так что логично было бы ему хотеть побыстрее)
Я вначале прочитал русскую версию, и там было "случайный". Когда стал разбираться, и прочитал в английской версии "arbitrary", стало только хуже :)
Расскажите, пожалуйста, как решать L?
Переберем, какая вершина будет нижней, а из них самой левой в многоугольнике. Отсортируем все вершины, которые выше или на той же высоте и правее по углу относительно неё. Дальше динамика: до какой вершины дошёл многоугольник, какое подмножество цветов уже покрыто, добавляем по одному треугольнику.
Кто такой Е.В. Панкратьев?
Ни кто не знает?
Это было непросто, но за день наверное справиться можно.