→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
6 дней
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
6 дней
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 25.11.2024 05:11:33 (h1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











New rule learned after SRM668: "You can't challenge if you have non-positive point". That means if you let your point negative, you can no longer let it positive again :(
Hah, 250 was so nasty, I got challenged and tried 2 unsuccessful challenges :P.
You're right, man. Submitted correct solution in a few minutes, then thought about 1*2k case, if'ed it (of course, incorrectly) and got an unsuccessful challenge too.
How to solve 450?
Here's a quick sketch. Only consider the vertices v such that 0, 1 can reach v and v can reach 0, 1. Now for all primes k in the range 2 to 2000, try to color the graph in k-colors such that the following condition is satisfied: if we let c(u) denote the color of vertex u, then if u - > v, c(v) = (c(u) + 1)(modk).
(u - > v means that there is an edge pointing from u to v)
If this coloring succeeds, then the answer is Chores. If for all k it fails, the answer is Freedom. The proof for this is if the coloring succeeds, then all cycles in the graph must have length multiple of k, and this is bad.
Note: I'm the only person I know of who did anything similar to this. Most other solutions I saw or heard about found gcd of cycle lengths.
I used the same idea as you (I'm 'socketnaut' on TC), except that I don't check all of the primes separately.
You can do a single dfs from vertex 0, noting the depth at which each vertex is discovered. It is clear that vertices must be colored according to their depth modulo K, since each one is on the end of an edge from its parent.
Now we check the remaining edges u -> v, and for each one we compute
depth[v] - depth[u] - 1. To satisfy the condition you described, whatever K we pick must be a divisor of each of those values, so all we need to do is find their GCD.I also did this, but I failed in checking only the SCC containing 0 and 1 (funnily enough, I did add a check for this, but it was the wrong check).
If there is a k-route with any big length, then clearly you can make a cycle starting in 0 and ending in 0 with any big length (by summing a k-path from 0-1, then a k-path from 1-0). This also works the other way around: if 0 and 1 are reachable from each other and you can make a 0-0 cycle with any big length, then you can use that cycle to make a 0-1 path with any big length, so you have a k-route with any big length.
Checking connectedness is easy, so now we only need to test whether we can make 0-0 cycles with any big length. It's a known result from number theory that this happens if and only if you can find cycles with lengths such that gcd(lengths) = 1. I don't know how to prove this formally, but you don't need to look that far -- if such a set of cycles exists, you can find it by checking for cycles up to a certain smallish length (around 6000 or so, maybe smaller) using BFS.
Yet another (although similar) idea is to find some cycle containing 0 (say of length c), and then run a BFS on an augmented graph, where we record for each node u and 0 ≤ i < c whether there is a path of length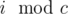 from 0 to u as can(u, i).
from 0 to u as can(u, i).
Then we only have to check whether can(1, i) for all i.
Story of my 250: I look at problem for a few minutes, I think it's pretty easy, but just in case I will go to Google. And I google for "hamiltonian cycle grid graph" and click the first link. Briefly skim the article, read that
Okay, about to code this. Wait, what about R = 1 case? No matter how I try, I cannot construct a Hamiltonian cycle for R = 1 C = 4 (obviously, endpoints have degree 1...). It must be a trick. I should hardcode R = 1 C > 2 case in. I thought "good thing I caught a bug before I mindlessly coded what I Googled".
Unfortunately I challenge a solution with similar case and unexpectedly got unsuccessful. I was confused for a few minutes, before realizing my code is wrong. Then I decide to bet everything on challenging 450, unfortunately my own 450 was challenged and my score became negative. Lesson learned, don't think, just code, even if reasoning is wrong it will still lead to correct answer.
In 250, you needed a Hamiltonian path, not a Hamiltonian cycle ("Liz can begin and end on any cell", and also explanation to Example 2).
Wouldn't there be a Hamiltonian path in every grid graph?
Yes, a path always exists. So, for starters, googling for "hamiltonian cycle grid graph" was irrelevant to the problem.
The quoted statement is true only in a context where m>1, n>1. Funny how a wrong statement from a wrong Google search could have helped solve the problem if taken on trust.
As they (don't) say, two wrongs make a right :)
I had mistakenly thought that to paint it K layers, we should probably paint one layer, then the second layer, and so on (interestingly, one would do that in real life, to let the paint dry out evenly). And the sample case with 1 2 2 followed my "rule", so I didn't notice anything bad.
can anyone help me with some ideas about D2 1000?
I believe my solution is not optimal, but anyway, here's the idea:
Khas at mostd=240divisors, and thus something with complexity O(N·d2) should passPlease explain your approach a bit more
very similar problem: 567C - Геометрическая прогрессия
Originally I wanted to have the 450 be a D1 hard, where it just asks for a k-walk from 0 to 1. It turns out this is at least as hard as determining whether there is a solution to a Chinese Remainder Theorem instance when there are multiple possibilities for each modulus, e.g.
x ≡ 1 or 5 (mod 6)
x ≡ 7 or 8 or 9 (mod 11)
x ≡ 12 (mod 27)
But I couldn't solve this problem. Does it have a known solution?
When k ≥ n2, to check existence of a k-walk, it suffices to calculate GCD of lengths of all accessible cycles and length of path from 0 to 1.
For k < n2, there is a trivial a O(km) solution simulating all steps. It may be possible to squeeze in the time limit with n and m up to 2000, as in the given problem, perhaps as some O(km / 32).
Ну и как ты собираешься битсетами делить время на 32 при просмотре M ребер? Я понимаю там, поделить на 32 для обновления вершин, достижимых из одной вершины, а как разные ребра с разными "смещениями" делить на 32?
Расскажи, пожалуйста. Очень интересно.
What is length of a path from 0 to 1? There are many of them, I don't know how it could be involved in doing some GCD and length of that path changes when we are taking into account different cycles, because to include cycle into 'GCDing' we have to "touch it". Note that we may not be able to simply return from 1 to 0 and use all cycles which we want. I'm very dubious about that solution.
By accessible cycles, I mean the cycles which are reachable from the source vertex and from which we can reach the target vertex.
Alright, here's my formal claim: the set of k ≥ n2 for which a k-walk exists can be expressed as {p + t·g} for all non-negative integers t, where
p ≤ n2 is some constant, and
g is the greatest common divisor of lengths of all accessible cycles.
Edit: as discussed below, this claim is in fact false for k-walks, but true for k-routes.
Definitely not true exactly because of reason I explained. If that reason was too vague, here is specific counterexample.
Consider such graph with such edges:
1->2->3
2->4->2
1->5->3
5->6->7->5
and we consider paths from 1 to 3.
You are right! That's a case I didn't think about.
Still, I'm fairly certain about my claim when applied to k-routes (paths from source to target and then back), not k-walks. Then, accessible cycles remain accessible, ever, regardless of where we are — unless we go to a vertex with no path to target, which we don't want to do anyway.
Yes, regarding to k-routes you are right, but that's why analogous solution to D1-450 is correct and that slight difference of ability to come back is what makes very hard problem from a fairly easy one :).
Согласен, Гасса, надо бы объяснение еще и того момента, что мы считаем НОД не только длин циклов, но и пути между 0 и 1, а что если путей таких много? Какой в подсчет включать? =))
Actually, very similar problem just appeared at Polish contest Algorithmic Engagements. We were given an automata up to 200 nodes and were asked for any k such that all runs of length k are accepted (or state that it does not exist).
(Don't ask me about solution.)
Извините, тупанул :)
0 недостижим из 1