Блог пользователя riadwaw

SRM 507
Автор riadwaw, 13 лет назад, По-русски

Сегодня в 20:00 MSK

Регистрация уже началась

  • Проголосовать: нравится
  • +17
  • Проголосовать: не нравится

13 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится
Кто-то знает, какой лимит регистраций на сегодняшний матч?
→ Ответить
  • 13 лет назад, # ^ |
      Проголосовать: нравится +1 Проголосовать: не нравится
    На все матчи существует лимит. Думаю он такой же как всегда. Раньше это было 2000, сейчас чуть побольше. По моему 2200.
    → Ответить
    • 13 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится

      Вопрос как раз в том, какой он сегодня. Так как последнее время трудно сориентироваться. То поднимут, то опустят обратно, то квалы ТСО (где лимит другой), то еще что-то...


      → Ответить
      • 13 лет назад, # ^ |
          Проголосовать: нравится +21 Проголосовать: не нравится
        Сегодня 2250 лимит. На самом деле его пока еще ни разу не опускали, ну и потихоньку поднимаем.
        → Ответить
        • 13 лет назад, # ^ |
            Проголосовать: нравится +4 Проголосовать: не нравится
          Не думаю, что сегодня будет проблема с количеством участников. Все-таки:
          09:30 - 16:30 * IBM TechTrek and Excursion with Lunch SeaWorld

          → Ответить
          • 13 лет назад, # ^ |
              Проголосовать: нравится +1 Проголосовать: не нравится
            Темпы регистрации говорят, что, пожалуй, все же будет. Слот субботний самый популярный, да и количество АСМ-финалистов в общей массе участников вряд ли больше чем 10%.
            → Ответить
          • 13 лет назад, # ^ |
              Проголосовать: нравится 0 Проголосовать: не нравится
            2250, никаких проблем:)
            → Ответить
13 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится
Прикольно, сейчас реально можно видеть, кто кому что пишет лично (whisper).
→ Ответить
13 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится
Не подскажете какой МЛ на ТопКодере?
→ Ответить
13 лет назад, # |
  Проголосовать: нравится +7 Проголосовать: не нравится
Не хотел бы я быть на месте человека, которому надо составить максимально полный набор тестов к сегодняшней div1 500, с учетом того, какими разными способами народ пытался ее решить.
→ Ответить
13 лет назад, # |
← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

Неужели этот бред по медиуму у меня пройдет?

upd: не прошел
→ Ответить
13 лет назад, # |
  Проголосовать: нравится +1 Проголосовать: не нравится
Подскажите, пожалуйста, как решать последнюю див.2
→ Ответить
  • 13 лет назад, # ^ |
    ← Rev. 3   Проголосовать: нравится +3 Проголосовать: не нравится

    По ходу единственные два зашедшие решения представляют собой поиск в ширину :( как-то фигово
    → Ответить
    • 13 лет назад, # ^ |
      ← Rev. 2   Проголосовать: нравится +3 Проголосовать: не нравится

      мне кажется, можно поиграться с границами.
      то есть посчитать "в лоб" жадиной 
              int start = Math.min(initPos, goalPos);
              int end   = Math.max(initPos, goalPos);
              while (need > 0) {
                  res++;
                  int index = Arrays.binarySearch(squares, need);
                  if (index > -1) {
                      break;
                  }
                  index = ~index - 1;
                  need -= squares[Math.abs(index)];
              }
      запомнить это значение.
      а дальше пытаться перебирать квадраты (не более res итераций) вниз и вверх (до первых дырок).
      не уверен, что зайдет. но таковы мысли

      п.с: если минусуете, то объясняйте в чем я не прав, пожалуйста 
      → Ответить
    • 13 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится
      Я уж подумал, что у нас тесты плохие. Но на самом деле все нормально. Посмотрите, там не совсем поиск в ширину, случай, когда с одной стороны нет дырок, обрабатывается отдельно.
      → Ответить
      • 13 лет назад, # ^ |
          Проголосовать: нравится 0 Проголосовать: не нравится
        Не подскажете тогда, где выкладываются разборы. А то мой скилл получения решения задачи по чужому коду пока слаб:)
        → Ответить
        • 13 лет назад, # ^ |
            Проголосовать: нравится +5 Проголосовать: не нравится
          Через пару дней будет вот здесь: http://apps.topcoder.com/wiki/display/tc/Algorithm+Problem+Set+Analysis.

          Но в целом решение довольно простое:

          1) Если между начальной и конечной позицией есть дырка, то -1.
          2) Если слева и справа от начальной и конечной позиций есть дырки, то поиск в ширину успевает (потому что не более 100 тысяч состояний и ~sqrt(100000) ходов из каждого).
          3) Если слева или справа нет дырки, то фактически ходы никак не ограничены. Посмотрим разность d между начальной и конечной позицией. Если это точный квадрат, то хватит 1-го хода. Если d = x^2 + y^2 (проверим в лоб), то достаточно 2-х ходов. Если d -- нечетное, то тоже хватит двух ходов, потому что (x+1)^2 - x^2 = 2*x+1. Если d делится на 4, то снова хватит двух ходов, потому что (x+2)^2 - x^2 = 4*(x+1). Иначе d дает остаток 2 при делении на 4. Двух ходов хватить не может (потому что каждый квадрат дает остаток 0 или 1 при делении на 4, соответственно разность двух квадратов даст остаток 0, 1 или 3). Поэтому надо 3 хода (сначала делаем d-1 за два хода, потом добиваем за последний ход до d).
          → Ответить
        • 13 лет назад, # ^ |
          ← Rev. 3   Проголосовать: нравится +3 Проголосовать: не нравится

          выкладываются здесь:
          попытаюсь объяснить как это вижу я.
          как я понял: сначала проверяется ситуация, чтобы между исходной и конечной точками не было дырок. если есть - возвращаем -1.

          далее обозначим start как min(init, goal), а end как max(init,goal)
          проверяем (end - start) в квадратах от 1 до 106. если нашли - возвращаем 1 (т.к. достаточно одного перехода из начала по квадрату в конец)

          далее ищем координату minHole дырки, ближайшей к min слева и координату maxHole дырки, ближайшей к end справа.

          если minHole или maxHole не существуют, то мы не ограничены для переходов по любым квадратам влево или вправо (до + - бесконечности), то если (end - start) нечетное - достаточно двух переходов
          чтобы понять это - напиши на бумажке все квадраты и заметь, что разница между ближайшими квадратами составляет арифметическую прогрессию (3, 5 ,7 ,9, 11, 13, 15, 17) . из этого ряда видно, что любое нечетное можно составить одним из квадратом + единица => возвращаем 2. 

          ну а дальше, если все предыдущее не сработало - отрабатывает уже поиск в ширину

          upd. пока писал, ответили. жаль
          → Ответить
13 лет назад, # |
  Проголосовать: нравится -6 Проголосовать: не нравится
Как 1000 div 2? Граф делать побоялся, сильно много ребер....
→ Ответить
13 лет назад, # |
← Rev. 5   Проголосовать: нравится +13 Проголосовать: не нравится

Может кто-нибудь рассказать решение Div1-1000. Только 257*3 придумал, что очевидно много.
→ Ответить
  • 13 лет назад, # ^ |
    ← Rev. 3   Проголосовать: нравится +3 Проголосовать: не нравится

    deleted
    → Ответить
  • 13 лет назад, # ^ |
      Проголосовать: нравится +3 Проголосовать: не нравится
    На контесте мое неверное за 256 работало около 0.2 в арене. Так что 257 возможно и прошло бы, если ходить только по достижимым состояним. Там же делится на очень большую С.
    → Ответить
    • 13 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится
      У меня вроде все состояния достижимы. Значит какая-то не та динамика. Не могли бы вы рассказать 6-ую степень?
      → Ответить
      • 13 лет назад, # ^ |
          Проголосовать: нравится +3 Проголосовать: не нравится
        Прошу прощения, по здравом размышлении понял, что это была 7я степень. Хотя, возможно, она проходила быстро из-за того, что ВАшила. Чуть позже проверю в практис руме.
        → Ответить
  • 13 лет назад, # ^ |
    ← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

    Аналогично. Ты что придумал?
    UPD. Неравда, у меня вместо одной 25 - 25*3.


    → Ответить
    • 13 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится
      По перебирали разбиения, в общем за (не знаю точно сколько, но не очень долго) посчитали d1ijk - количество способов поставить в одну полоску i видного цвета и j,k невидных. Дальше достаточно очевидная динамика.
      → Ответить
  • 13 лет назад, # ^ |
      Проголосовать: нравится +11 Проголосовать: не нравится
    Сначала динамика с 5й степенью состояний внутри одного столбца - номер клетки, количество хороших, количество плохих, макс высота и высота в текущей клетке - пересчет за О(1). Получаем из нее массив (кол-во хороших, кол-во плохих) -> число вариантов в ряду
    Потом динамика с 3й степенью состояний (номер столбца, кол-во хороших, кол-во плохих) и пересчетом за квадрат.
    Потом просто выбираем хороший цвет, запускаем динамику и домножаем ответ на С(кол-во плохих, кол-во одного из плохих)
    → Ответить
    • 13 лет назад, # ^ |
        Проголосовать: нравится +8 Проголосовать: не нравится
      А, да, если 3 раза динамику запускать это все еще не проходит, надо получить из динамики массив и запустить ее для 25, 50. Тогда у меня работает 1.3 с на макс тесте
      → Ответить
  • 13 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    3· 257 можно превратить в 257, если один раз динамику считать, а не 3.

    Просто из неё нам три элемента понадобятся.

    А ещё 257 можно превратить в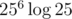 , что после некоторых оптимизаций проходит за 1.3 секунды.

    → Ответить
13 лет назад, # |
← Rev. 3   Проголосовать: нравится -16 Проголосовать: не нравится

Йа-ха! В прошлый SRM был впервые в жизни сданный hard, в этот - впервые в жизни 1 место в комнате =)
Upd. Дабы выдать хоть какую-то полезную информацию, скажу, что многие в medium пытались подобрать параллелепипед с квадратным основанием. Это неверно: контрпример - {33, 1, 3}, правильный ответ - 60.
→ Ответить
13 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится
Заполз таки обратно в желтые. Ровно - 1500 :)
→ Ответить
13 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится
расскажите, пожалуйста, решение 500
→ Ответить
  • 13 лет назад, # ^ |
    ← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

    А, ну вот, см. коммент ниже. И коль скоро это предположение верно, то идём по увеличению объёма, начиная с суммы объёмов всех кубиков, и для каждого генерируем все возможные подходящие параллелепипеды - а их максимум где-то 310 (разбиение объёма на три множителя) - и смотрим, можно ли в такой параллелепипед упихать сколько надо больших кубиков.
    → Ответить
  • 13 лет назад, # ^ |
      Проголосовать: нравится +8 Проголосовать: не нравится
    Ответ лежит между L*L*L*Nb + Ns и L*L*L*Nb + Ns + L*L (все выстраиваем в столб с основанием L*L). Для каждого числа из этого диапазона проверим, можем ли построить параллелепипед с этим объемом, вмещающий Nb больших кубиков. Заметим, что длины его сторон - делители числа значения объема, которое мы сейчас проверяем. Перебираем две стороны из набора делителей, находим третью, проверяем, влезут ли в такой параллелепипед Nb больших кубиков. Сложность L^2 * (количество делителей ответа) ^ 2.
    → Ответить
  • 13 лет назад, # ^ |
      Проголосовать: нравится +3 Проголосовать: не нравится
    Я перебирал две стороны паралелепипеда: Так как ответ влазит в знаковый инт 32, т.е. максимум 2 в 31. Поэтому я внешний цикл делал до корня третьей степени из 2 в 31, а внутренний до корня второй степени, это выходит коло 50 лимонов операций в общем. Третьей стороной я брал сначала с = (Ns + Nb*L*L*L)/( a * b) . где a и b перебираются предыдущими циклами, а потом с+1. И каждый раз проверял, что я могу в этот параллелепипед уместить все большие кубы. т.е  (a/L) * (b/L) *(c/L) >=Nb.
    → Ответить
  • 13 лет назад, # ^ |
      Проголосовать: нравится +3 Проголосовать: не нравится
    А можно так - перебираем 2 меньшие стороны и рассчитываем третью так, чтобы влезло
    → Ответить
    • 13 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится
      Ну вот так я пытался делать, но перебирал мало, как оказалось)
      → Ответить
      • 13 лет назад, # ^ |
          Проголосовать: нравится 0 Проголосовать: не нравится
        Надо было так - очевидно меньшая сторона меньше кубического корня из текущего ответа, следующая меньше квадратного корня из ответа делить на меньшую сторону
        → Ответить
13 лет назад, # |
← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

Но всё-таки было бы неплохо до конца разобраться с Div. 1 500. Моё решение основывалось на предположении, что ответ ненамного больше числа Ns + Nb * l3, - и это оказалось правдой. На тесте с максимальным временем работы разница составляет 99. Видимо, это значит, что в худшем случае она O(l2). Но почему?
→ Ответить
  • 13 лет назад, # ^ |
    ← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

    наврал
    → Ответить
    • 13 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится
      Да, благодарствую, и volkhin тоже. И как я не увидел такую элементарную вещь?.. Расскажите лучше, почему же Ваше решение упало. Я мельком глянул и понял, что Вы перебираете длины двух сторон и подгоняете третью. Разве это неверно?
      → Ответить
      • 13 лет назад, # ^ |
          Проголосовать: нравится 0 Проголосовать: не нравится
        Я перебираю 2 длины, но перебираю их мало(чтоб успевать в TL), такое не проходит, либо есть TL, либо есть WA.
        Я собственно не особо в него и верил)
        → Ответить
  • 13 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится
    http://codeforces.net/blog/entry/2067#comment-40537
    → Ответить