Задача А
Разберем два случая t = 10 и t ≠ 10.
Если t = 10, то либо n = 1, и тогда ответ - 1 (очевидно, что среди чисел от 1 до 9 нет делящихся на 10), либо n > 1, и тогда первые n - 1 цифр можно заполнить как угодно, а в конце дописать 0.
Если t < 10, то просто заполним все число цифрами t и оно, очевидно, будет делиться на t.
Задача B Количество способов рассадить всех гномов — 33n. Посчитаем количество способов рассадить гномов так, чтобы в любом треугольнике гномы получили 6 монет, а потом вычтем это число из всех способов. Заметим, что все гномы однозначно разбиваются на треугольники вида i — (i + n) — (i + 2n), i < n. Поэтому можно посчитать количество способов независимо по каждому треугольнику, а потом перемножить результаты. Чтобы получить ответ для треугольника, осталось заметить, что существует ровно 7 способов взять гномов с 6 монетами (это все перестановки 1, 2, 3 и 2, 2, 2)
Итого ответ — 33n - 7n. Посчитать степени можно за O(n).
Задача С
Построим строку, которая не отличается на t, а совпадает в k = n - t символах. Пусть строки s1 и s2 совпадают в q символах. Тогда если k ≤ q, то возьмем любые k позиций, в которых s1 и s2 совпадают, и поставим в ответ такие же символы. Во все остальные n - k позиций поставим символы, отличающиеся от соответствующих в s1 и s2 (мы всегда можем так сделать, так у нас 26 букв).
Теперь k > q. Тогда, если есть ответ, в котором в какой-то из этих q позиций в ответе стоит не такой же символ, как в s1 и s2, то сделаем его равным им, а в каких-нибудь позициях, где s1i ≠ s2i, s1i = ansi (и наоборот) поставим в ansi символ, отличный от s1i и s2i(это можно сделать, так как k > q). Тогда можно сразу в эти q позиций поставить символы, равный соответствующим в s1 и s2. Теперь у нас есть строки s1 и s2 длины n - q, отличные в каждой позиции, и надо предъявить строку ans такую, что f(ans, s1) = f(ans, s2) = k - q. Так как строки s1 и s2 отличаются во всех позициях, то любой символ из ans равен либо соответствующему в s1, либо соответствующему в s2, либо ни одному из них. Поэтому, нам надо хотя бы 2(k - q) символов в ответе, чтобы сделать f(s1, ans) = k - q и f(s2, ans) = k - q. Следовательно, если n - q < 2(k - q), то решения не существует. Иначе просто жадно в первые k - q символов ответа поставим символы из s1, в следующие k - q символы из s2, а остальные заполним символами не из s1 и не из s2.
Асимптотика — O(n).
Задача D
Общеизвестно, что между двумя соседними простыми числами, которые меньше 109, расстояние не очень большое. На самом деле для n = 109 максимальное из этих расстояний равно 282. Поэтому будем делать так: найдем наибольшее число p, такое что p < n - 1 и p — простое. По нашему утверждению n - p < 300. Скажем, что p входит в разложение n и теперь надо разложить четное(так n — нечетное и p — нечетное(если не 2)) n - p на сумму двух простых. Так как n - p маленькое, то сделаем это, просто перебрав два простых. То, что для всех четных, меньших 300, существует разложение на не более чем два простых, можно было проверить просто написав перебор.
Задача E
Будем считать, что все мы платим за обмен не |i - j|, а 2|i - j|. Тогда можно считать, что мы платим |i - j| за перемещение pi и |i - j| за перемещение pj. Тогда, если x изначально был на позиции i, а потом пришел на позицию j, то мы заплатим за него хотя бы |i - j|. Поэтому ответ это хотя бы 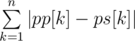 (pp — позиция k в перестановке p, а ps — позиция k в перестановке s). Докажем, что это и есть ответ конструктивно, предъявив алгоритм.
(pp — позиция k в перестановке p, а ps — позиция k в перестановке s). Докажем, что это и есть ответ конструктивно, предъявив алгоритм.
Будем считать, что перестановка s отсортирована (нашу задачу легко свести к этой). Тогда будем последовательно(сначала n, потом n - 1 и так далее) переставлять числа на свои позиции. Как поставить n на свою позицию? Пусть оно стоит на позиции pos. Докажем, что среди чисел, стоящих справа от n, есть число, меньшее или равное pos(дальше поменяем его местами с n — от этого оба числа сдвинутся к своим итоговым позициям, и при этом n сдвинется хотя бы на 1 вправо, поэтому можно дальше делать так же). Заметим, что всего справа от n ровно n - pos чисел. При этом сколько из них могут быть больше pos. Казалось бы, тоже n - pos, но это не так, так как число n, большее pos, стоит не правее, чем n :). Поэтому, по принципу Дирихле, найдется число, которое меньше или равно pos, и стоит справа от n.
Как теперь реализовать этот алгоритм за O(n2), а не за куб? Вот мы хотим поставить n на свое место. Идем направо указателем, пока не встретим число, меньшее или равное pos, а потом поменяем n с этим числом. Дальше указатель надо пускать уже от новой позиции n, поэтому указатель всегда двигается только вправо, и суммарно пройдет не больше n. Итак, каждое из n чисел мы ставим на свою позицию за O(n), поэтому получаем O(n2).










Почему кол-во способов рассадить гномов равно 3^(3n)?
Есть 3*n гномов. У каждого 1, 2 или 3 монеты — 3 варианта. Правило произведения — 3^(3*n).
потому что количество способов раздать 1, 2 или 3 монеты: Одному гному — 3. Трем гномам — 3 ** 3 = 27 N тройкам гномов — 3 ** (3 * N)
Problem D is clone of Timus #1356 ? But task C is more difficult than D . . .
Можно объяснение почему в задаче D выбор одного из чисел в разложении, как наибольшего простого <= нашего числа всегда ведёт к правильному ответу?
Бинарная проблема Гольдбаха. Вообще, большинство просто отняло 3 и раскладывало получившееся четное число.
я свел к бинарной проблеме, но ее не решил. Как она решается?
Просто генерируем решетом все простые числа до некоторого предела, а затем для каждого M из них проверяем, правда ли, что M — N простое. На самом деле, проверить нужно очень немного чисел, потому что у случайного числа вероятность быть простым ~ 1/log(N).
Решето генерируется долго, у меня оно падало по времени (на 10 ** 8). Я просто отнял 3 и влоб искал разложение через обычный алгоритм простоты до корня. Так зашло.
Решето надо генерировать до небольшого предела (я все равно перестраховался и взял 10^6), и число M чаще всего не больше сотни.
Ах, я неправильно понял. Проверка второго числа не по решету выходит, а другим способом.
Спасибо =)
Задача D: Зашло такое решение:
Но я не смог доказать, что для второго случая всегда выполняется: n = a + 2b, где a, b — простые. Есть кто действовал так же?
Действовал так же, но во время контеста тоже не доказал.
Оказывается, есть такая гипотеза http://mathworld.wolfram.com/LevysConjecture.html
Интересная заметка, и там есть ссылка на обсуждения с кодом проверки до 10^9: https://groups.google.com/forum/?hl=en#!msg/sci.math/HoCpH8gPDHM/gtU-fuSWnFMJ. В принципе, можно проверить до немного большей границы, или проверять случайные числа с помощью BPSW.
Thanks for the awesome round! :)
BTW, there is a typo in Problem D's description:
"More formally, you are given an odd numer n." ->
"More formally, you are given an odd number n."
Д — очень хорошая задача.
Д — очень баян-задача.
Whats proof for greedy method used for problem D ?
http://sweet.ua.pt/tos/goldbach.html
If we modify the 584C - Marina and Vasya to find
but not
, what is the fast solution to the new problem?
For example, "aaabbc" is different from "bbcaad" in exactly 1 characters in the new "difference rule" because one permutation of "bbcaad" is "aadbbc". The difference between s1 and s2 in the new problem may be calculated like this:
And it seemed that we can use the character c with minimal cnt[c] to "provide difference" firstly if we want to build a second string.
Didn't the question tell us to find a third string different from them in exactly t characters (irrespective of positions) i.e. your modified version?
Please correct me if I am making some mistake.
So I wasn't the only one with the same confusion. Here is what the author wanted to mean:
If am not wrong, the difference in problem C was based on the characters at the same positions. The difference in my modified version is based on the count of each character irrespective of positions. If what you said is about the modified version, I think you are correct.
where's the proof of correctness for Problem D ?
Goldbach's Conjecture
also Goldbach's_weak_conjecture
I have a questions considering problem E. 1. Why is the problem of transforming permutation p to s equal to problem of transforming permutation p to (1,2,...,n)? 2. Shouldn't it be "Let's move the pointer to the right until number becomes lower or equal to pos."
Interesting 584E. While I keep getting TLE for printing output with std::cout, the same test case could be finished in <200ms by printf...
Are there any method to significantly speed up std::cout?
ios_base::sync_with_stdio(false);cin.tie(0);I can't find C like difficult problem, more like hard to implement problem.
Actually, I think that it becomes somewhat easier to implement if you first set the output to something completely different from both strings a and b and then iteratively refine it, always maintaining the invariant that it is equidistant from a and b.
It's not hard to notice that, at each step, you must either change an element i such that ai = bi or change two elements i, j such that ai ≠ bi and aj ≠ bj. For more details, take a look at this code: http://codeforces.net/contest/584/submission/13449413
Nice implementation. Clear and straightforward.
Easy to understand.
I solved D by using 3 every time. I precomputed primes up to 10^6 and then tried to find the first prime p for which (n-p-3) is prime. It is always found fast enough (31 ms runtime, actually), but I have no proof of why it works.
http://codeforces.net/contest/584/submission/13480500
This also follows from Goldbach's conjecture (if it were proven), n - 3 is even so there should be two primes p1, p2 such that n - 3 = p1 + p2, or n - p1 - 3 = p2.
Yes, but there is no proof that those two primes (or at least one of them) are <= 10^6.
Well ..
https://en.wikipedia.org/wiki/Goldbach%27s_conjecture#Verified_results
If you read Wikipedia's article on Goldbach's conjecture they claim:
"3325581707333960528 is the smallest number that has no Goldbach partition with a prime below 9781".
Although I haven't gone to the source of this verification so I don't know whether it's actually true.
Notice this implies your 'search for the first prime..' part will try -possibly much- less than 10000 possible partitions.
That's funny, I literally read the whole "Verified results" section except for this last sentence. Also that's a really interesting fact, I definitely wouldn't have guessed that primes are this common. Bad intuition on my part, I guess.
This theorem might be of interest: https://en.wikipedia.org/wiki/Prime_number_theorem. Roughly, in the neighborhood of n, you can expect about one in every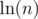 numbers to be prime. Knowing this is occasionally useful when analyzing (or designing) "brute force" algorithms that would otherwise seem to give TLE.
numbers to be prime. Knowing this is occasionally useful when analyzing (or designing) "brute force" algorithms that would otherwise seem to give TLE.
On a related note, it seems that Google once posted several recruitment billboards with the text "{first 10-digit prime found in consecutive digits of e}.com". Turns out the expected solution was just to brute force the possible sequences :)
Source: http://mathworld.wolfram.com/news/2004-10-13/google/
Can someone explain me how did he get The number of ways to choose ai = (3)^(3*n) in Problem B.
each element of a can have one of three values (1 or 2 or 3), and the number of elements of a is 3*n so the number of ways to choose the values of a = 3^(3*n)
“You can check that there is a solution for all even numbers less than 300 by bruteforce.” Actually,there is a solution for all even numbers less than 10^18. https://en.wikipedia.org/wiki/Goldbach%27s_conjecture
Can somebody explain how E solution works? I didn't understand very well the tutorial, sorry :/
Thanks.
Sure :)
Let a and b be two permutations of length n and suppose that we want to transform a into b. Now, let sx denote the position to which we want to move the value x in a -- in other words, sbi = i. The first thing to notice is that the theoretically best value for the answer is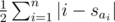 . The only way to reach it would be to move each element ai to the position sai without ever getting farther from it. And indeed, it turns out that we can always do that!
. The only way to reach it would be to move each element ai to the position sai without ever getting farther from it. And indeed, it turns out that we can always do that!
If we sequentially process elements from the right, a possible strategy is the following: visit one element at a time and, if it should be to the right, try to move it to its final position by performing swaps along the "good pairs" on the path between it and its destination. I'm calling a pair (ai, aj) "good" if swapping ai and aj moves them both closer to their final positions. (Remember, swapping a pair that isn't good would make it impossible to reach the optimal value.)
Here's my implementation: http://codeforces.net/contest/584/submission/13502664 (s in the explanation corresponds to desired_pos in the code)
johnjq , thanks for the excellent explanation, now I understood!
mras, you're welcome :)
How to prove that the solution for the problem E requires the smallest amount of money?
Because solution moves numbers only to their positions in final array
А если много вариатов будет,тогда че делать?
Если возможных ответов несколько, разрешается вывести любой.
Every problem of this contest is beautiful and mathematical.
For problem D , how you have figured out maximal distance is 282?
you don't need to calculate that just we need to know that this fact exists!!
B is solvable using Binary Exponentiation in O(log(n)) https://codeforces.net/contest/584/submission/55737018
why do we need (pot_27-pot_7+MOD)%MOD? why just (pot_27-pot_7)%MOD won't work?
Edit : Figured, it's different for minus.
For problem C, Why "cdd" is not a valid solution for first test case? https://codeforces.net/contest/584/submission/68720559