Всем привет!
Совсем скоро, 25 октября состоится интернет-тур Всероссийской командной олимпиады школьников по программированию.
Узнать о ней больше можно здесь.
Предлагаю после контеста обсудить задачи.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Всем привет!
Совсем скоро, 25 октября состоится интернет-тур Всероссийской командной олимпиады школьников по программированию.
Узнать о ней больше можно здесь.
Предлагаю после контеста обсудить задачи.
| Название |
|---|



На всякий случай добавлю, что задачи будут те же, что и на Петербургском отборе, так что его тоже можно обсудить тут :)
А может стоит перенести раунд? т.к. он пересекается с отбором на ВКОШП.
Что-то мне подсказывает, что он будет проводиться по задачам СПбКОШП :)
Вопрос командам из Казахстана. Кто-нибудь получал логины на пробный тур?
"Как только ИТМО выдаст пароли — вышлю", (с) Артем Игликов
ладно господа начну как решается задача К
Идея в целом — динамическое программирование. введем динамику dp[i][j] = rage. i — сколько первых полос машин обработали. j — сколько в сумме пропустили машин за один проход. rage — минимальная суммарная ярость за все время водителей первых i полос. Если пропускать с этих первых i полос по j машин то база динамики — dp[0][0] = 0. Переходы — dp[i][j] = min(dp[i-1][j-k] + rage(i,k)), k = 1..j , где rage(i,k) — суммарная ярость водителей i-oй полосы за все время, если гнать по k машин за один проход то в отдельной матрице previ сохраняем оптимальный переход. Потом по этому массиву восстанавливаем ответ.
Работает за O(n*(k^2)).
Фууу, на Java не заходит по памяти) Лонги размером [100_00][300] занимают 306мб вместо 228мб. Меньшим размером предподсчета удалось набрать максимум TL 34. Мелочь, а неприятно. На С++ все заходит
Откуда берётся такой размер массива?
Первое это ci, кол-во машин, второе это ki, количество пропусков. dp[ci][ki] = ci * (ci — 1) / 2 + dp[ci — ki][ki] при ci >= ki. Это значения rage(i,k) у LonelyCoder
То есть там две динамики, вторая динамика это поиск ответа за n*k^2
А, проблема в том, чтобы посчитать именно rage(i, k) ? Ну можно вывести формулку для этого, не обязательно считать это динамикой
Как решать B?
Когда день рождения у Шерил? Баянище среди математиков :)
На глаз, просто написать программу, которая будет решать загадку. Моделировать сообщения из диалогов по очереди, должно зайти.
Будем рассматривать “common knowledge”, т.е. факты, известные всем, кто наблюдает комментарии Ани и Бори.
Первое утверждение Ани: “Я не знаю точную дату рождения Вани, но я уверена, что и Боря её тоже не знает”. После него все узнают следующее: для числа, которое знает Аня, существует несколько (> 1) подходящих месяцев (поскольку она не знает точную дату), притом для каждого из этих месяцев существует несколько (> 1) подходящих дней (поскольку она говорит, что точно знает, что Бориной информации недостаточно). Назовём все дни (= числа 1..31), которые подходят под это условие, Аниными днями (NB: их много! среди них точно есть день, который Ваня назвал Ане, но есть и левые).
Первое утверждение Бори: “Я сначала не знал дату Ваниного рождения, но теперь, после твоего комментария, знаю точно!”. Узнаём следующее: для месяца, который знает Боря, существует несколько подходящих дней, но ровно один из этих дней является Аниным днём. Назовём все такие месяца Бориными месяцами (аналогичная NB).
Второе утверждение Ани: “Ого! Теперь и я тоже знаю точную дату!”. То есть среди месяцев, которые соответствуют известному Ане дню (который точно является Аниным днём), есть только один Борин месяц. Назовём все Анины дни, для которых это верно, эээ, супераниными днями.
Поскольку мы формализовали всю доступную нам информацию и известно, что с её помощью можно однозначно определить день рождения Вани, существует ровно одна пара (супераниндень, Борин месяц), которую можно найти в инпуте. Её и выведем.
Какая фул идея на E?
Разделим a на 2 части, каждое будет максимум до миллиона. В первой части для каждого остатка от деления на b запишем минимальное количество измененных цифр, для второй части доберем остаток от деления из первой. O(sqrt(N)). Подсказывают, что если вначале перебирать вторую половину можно обойтись без map, так как остатки от деления на b не превысят корня.
Мы делали так: если M до 104, то, очевидно, что среди n...n + 10000 есть хоть одно число, которое делится на M, поэтому в ответе изменено не более 4 цифр, их можем перебрать (C[11, 4] × 104 = 3300000, норм). Если же M больше, чем 104, то существует где-то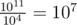 подходящих кратных M, можем попробовать каждый из них.
подходящих кратных M, можем попробовать каждый из них.
Если M <= 10^6, можно написать динамику dp[len][mod], иначе просто перебираем все числа кратные M.
Кто нить может отправить ссылку результатов с Казахстана ? Заранее спасибо.
Всё еще frozen.
вот окончательные результаты Казахстана
как решать С
Вот код: pastie.
В целом идея такова: ставим на строку в промежутке [rb — 10^5, rb + 10^5]. Каждую строку делим на полоски по запрещенным, и в каждой решаем отдельно.
Допустим, что нам известно, что места с a-того по b-тое в ряду r свободны, и мы хотим найти в них неудачность оптимального расположения для k шушпанчиков (r - l + 1 ≥ k).
Интуитивно понятно, что есть три возможных оптимальных варианта расположения: так, что cb находится посередине выбранного отрезка (в случае чётного k этот случай распадается на два) или так, что отрезок касается одной из границ отрезка a... b. Любой другой отрезок длины k можно подвинуть влево или вправо, и это уменьшит его неудачность.
Неудачность считаем отдельно по рядам и по колонкам. Каждое из этих мест находится на расстоянии |r - rb| по рядам от лучшего, так что общая неудачность по рядам — |r - rb| × k. А по колонкам получается либо одна арифметическа прогрессия (если rb строго слева или строго справа обеих границ выбранного отрезка), либо две (если rb принадлежит выбранному отрезку).
Существует не более 105 рядов, в которых есть занятые места — можем отсортировать занятые места, и тогда каждый ряд разобьём на некоторое количество свободных отрезков (в сумме порядка 105 отрезков), оптимальное расположение в каждом из которых можем посчитать (за константное время) так, как описано выше.
Остаётся порядка 109 рядов, в которых не занято ни одно место, но ясно, что нас интересует только тот свободный ряд, который ближе всех к лучшему месту — можем завести булевский массив [-100000..100000], который будет соответствовать рядам на расстоянии не более 100000 от ряда лучшего места, и во время чтения отмечать все ряды, в которых занято хоть одно место — поскольку занято только 105 мест, то в этом массиве сможем найти самый близкий совершенно пустой ряд. Его тоже проверим так, как описано выше (положив a = 1, b = n).
как решать H?
Попробуем решать стандартную задачу, то есть просто искать Гамильтонов цикл минимального веса (это делается стандартной динамикой f[mask][last]).
Сделаем только одну модификацию: заметим, что после того, как в mask
есть какое-то количество единичных битов (обозначим за cnt) такое, что
cnt есть сумма размеров нескольких первых групп, то нужно вернуться в 0 (это значит, что
очередной человек завершил свой обход).
Код: http://ideone.com/J0S8DC
Кто нить может отправить ссылку результатов команд с Москвы?
Заранее спасибо.
Разбор все задач: ссылка 1
Тесты, решения жюри и исходные тексты условий: ссылка 2
Любопытно: в условии задачи E написано «Леша уже попробовал решить пример, но, неожиданно для себя, понял, что n на m не делится.», однако в тестах 29, 30, 35, 36, 41 и 42 это условие не выполняется.
Да, в легенде действительно так, скорее всего ошибка. Но под формат выходныз данных все подходит: ~~~~~ В единственной строке выходного файла выведите одно целое число — результат изменения минимального числа цифр в числе n, чтобы полученное число не имело ведущих нулей и делилось на m. ~~~~~