Мне нравится идея Endagorion дополнять разбор задач небольшими упражнениями, связанными с подготовкой задачи, её обобщением или наличием более эффективного решения. Попробуем и мы предложить читателю подобные вопросы по некоторым задачам.
Div. 2A (Поединок волшебников)
Автор идеи: Роман Гусарев, разработка: timgaripov.
Найдем координату первого столкновения импульсов. Они сближаются со скоростью p + q, а значит первое столкновение произойдёт через 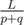 секунд. Следовательно, координата первого столкновения может быть вычислена как
секунд. Следовательно, координата первого столкновения может быть вычислена как 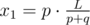 .
.
Заметим теперь, что расстояние проходимое импульсами на обратном пути до волшебников равно расстоянию проходимому ими от волшебников до места первой встречи. Это значит, что импульсы вернутся к волшебникам одновременно, и ситуация станет идентична изначальной. Таким образом, вторая встреча (и все последующие) произойдёт в той же точке, что и первая.
Пример решения: 13836780.
Div. 2B (Ребрендинг)
Автор идеи: glebushka98, разработка: thefacetakt.
Тривиальное решение: будем эмулировать работу дизайнеров, а именно каждый раз ходить и честно перекрашвать все xi в yi и наоборот. Работает за 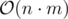 , получает TL.
, получает TL.
Попробуем улучшить этот результат.
Заметим, что одинаковые буквы переходят в одинаковые. Это означает, что позиция буквы никак не влияет на результат, и достаточно помнить для каждого возможного значения символа, во что он перейдёт. Пусть p(i, c) — символ, который будет стоять вместо всех вхождений c после обработки i дизайнеров. Тогда:
- p(0, c) = c
- Если p(i - 1, c) = xi, то p(i, c) = yi
- Аналогично, если p(i - 1, c) = yi, то p(i, c) = xi
Данное решение работает уже за O(|Σ|·m + n) и проходит все тесты.
Упражнение: доведите решение данной задачи до сложности O(Σ + n + m).
Примеры решения: 13837577 за O(|Σ|·m + n) и 13839154 за O(|Σ| + n + m).
Div. 2C\Div. 1A (Медианное сглаживание)
Автор идеи и разработчик: Sender.
Назовём статичными точками позиции, которые не могут измениться, сколько бы раз мы не применяли к последовательности алгоритм медианного сглаживания. Оба конца являются статичными точками по определению. Также, легко заметить, что если рядом стоят два одинаковых символа, то обе эти позиции так же являются статичными точками.
Исследуем влияние статичных точек на соседние элементы. Пусть ai - 1 = ai, то есть элемемнты i - 1 и i являются статичными точками. Пусть также ai + 1 статичной точкой пока не является, следовательно ai + 1 ≠ ai и ai + 1 ≠ ai + 2. Из предыдущего предложения и того, что возможны только 0 и 1 делаем вывод, что ai = ai + 2 и после одного применения алгоритма медианного сглаживания будет выполнено ai = ai + 1. То есть любая статичная точка за один шаг превращает все соседние элементы в статичные точки. Таким образом, любая последовательность в итоге стабилизируется.
Остаётся только вычислить скорость стабилизации и результирующие значения. Заметим, что если между двумя статичными точками i и j нет других статичных точек, то это означает чередование всех символов между позициями i и j. Несложно проверить, что в чередующейся последовательности новые статичные точки не образуются, следовательно последовательность будет оставаться чередующейся пока до неё не дойдёт влияние одной из соседних статичных точек.
Итоговое решение: выделим все статичные точки в изначальной последовательности и найдём max(min(|i - sj|)), где sj — множество индексов позиций статичных точек. Сложность решения O(n).
Упражнение 1: взломайте решение честно моделирующее применение алгоритма медианного сглаживания до стабилизации процесса.
Упражнение 2: придумайте как ускорить квадратичное решение с помощью битового сжатия (и всё равно получить TL).
Примеры решений: 13838940 и 13838480.
Div. 2D\Div. 1B (Чип и Дейл спешат на помощь)
Автор идеи и разработчик: StopKran.
Заметим, что если собственная скорость дирижабля задана вектором (ax, ay), а скорость ветра вектором (bx, by), то реальный вектор движения дирижабля определяется как (ax + bx, ay + by).
Одним из ключевых моментов в решении задачи является понимание монотонности функции ответа по времени. Если дирижабль может достичь цели за  секунд, то он сможет достичь её и за
секунд, то он сможет достичь её и за 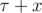 секунд, для любого x ≥ 0. Это очевидно вытекает из условия, что максимально возможная собственная скорость дирижабля строго превосходит скорость ветра в любой момент времени.
секунд, для любого x ≥ 0. Это очевидно вытекает из условия, что максимально возможная собственная скорость дирижабля строго превосходит скорость ветра в любой момент времени.
Поскольку функция ответа монотонна, воспользуемся методом бинарного поиска по ответу, а именно, научимся проверять для фиксированного параметра  , возможно ли добраться от точки (x1, y1) до точки (x2, y2) за время
, возможно ли добраться от точки (x1, y1) до точки (x2, y2) за время  . Будем учитывать перемещение под действием ветра и собственное перемещение отдельно. Найдём сперва смещение дирижабля вызванное ветром:
. Будем учитывать перемещение под действием ветра и собственное перемещение отдельно. Найдём сперва смещение дирижабля вызванное ветром:
- (xn, yn) =
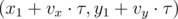 , если
, если 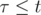 ;
; - (xn, yn) =
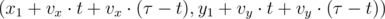 , если
, если 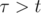 .
.
Остаётся только проверить, что используя только лишь собственную скорость можно добраться за время  из точки (xn, yn) в точку (x2, y2).
из точки (xn, yn) в точку (x2, y2).
Итоговая сложность: 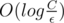 , где C — максимальная координата, а ε — требуемая точность.
, где C — максимальная координата, а ε — требуемая точность.
Упражнение 1: подумайте как решить задачу, в случае когда не гарантируется, что дирижабль всегда быстрее ветра.
Упражнение 2: можете ли вы решить задачу за время O(1)?
Примеры решений: 13838659 и 13842505.
Div. 2E\Div. 1C (Три государства)
Автор идеи и разработчик: haku.
Утверждение. Пусть в неориентированном невзвешенном связном графе выделенны три различные вершины u, v, w. Одна из минимальных сетей, связывающих выделенные вершины, выглядит как некоторая вершина графа c, возможно совпадающая с одной из выделенных, из которой исходят кратчайшие пути к каждой из выделенных вершин, причём эти пути являются вершинно-непересекающимися.
Доказательство. Одним из оптимальных связывающих подграфов обязательно является дерево. Действительно, в противном случае на любом цикле найдётся ребро, которое можно выкинуть, и это не ухудшит ответ, поскольку он не зависит от количества используемых рёбер. Листьями дерева могу являться только вершины u, v и w, иначе ответ можно было бы улучшить, просто выкинув такой листь. Дерево, у которого не более чем три листа, имеет не более одной вершины степени больше двух, которая и будет вершиной c из утверждения выше. Разумеется, любой путь от c до листа имеет смысл заменить на кратчайший. Отдельно возможен вырожденный случай, что дерево ответа — это бамбук, но в таком случае вершиной c является одна из трёх выделенных вершин (не лист).
Теперь имеем следующий метод для нахождения длины кратчайшей связывающей сети: перебрать все вершины, включая выделенные, и из сумм кратчайших расстояний от данной вершины до выделенных выбрать минимальную. Ясно, что таким образом мы переберём длины различных связывающих сетей, среди которых будет и длина кратчайшей, и поэтому минимум будет ответом.
Для сведения исходной задачи к задаче поиска минимальной связывающей сети, можно представить карту в виде графа, где вершинам соответствуют клетки, принадлежащие государствам или допускающие постройку дороги, а ребро между двумя вершинами ставится, если они являются соседними в таблице. Все вершины, соответствующие одному государству, необходимо сжать в одну. Несложно заметить, что исходная задача таким образом свелась к вышеописанной.
Примеры решений: 13843265 — описанное решение реализовано через бфс на 0-1 графе, 13840329 — здесь логика решения несколько иная, разбираются два принципиально разных случая.
Div. 1D (Сверхсекретное задание)
Автор идеи и разработчик: glebushka98.
Если 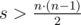 , то ответом является сумма k минимальных элементов.
, то ответом является сумма k минимальных элементов.
Пусть i1 < i2 < ... < ik — индексы элементов, которые войдут в итоге в ответ. Заметим, что относительный порядок выбранных элементов менять не имеет смысла, а значит, мы можем однозначно сказать, какой из выбранных элементов займёт какую позицию в ответе. T — минимальное количество операций, за которое их можно поставить на k первых мест. 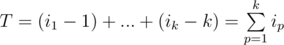 —
— 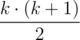 .
.
T ≤ S 
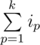 ≤
≤ 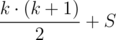 .
. 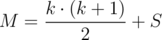 .
.
Посчитаем динамику d[i][j][p] — минимально возможная сумма, если среди первых i элементов выбрать j с суммой индексов не больше p. В целях оптимизации использования памяти будем хранить каждый раз только два верхних уровня динамики.
Итоговая сложность решения: O(n4) по времени и O(n3) по памяти.
Примеры решений: 13845513 и 13845571.
Div. 1E (День рождения)
Автор идеи: meshanya, разработчик: romanandreev.
Задача естественно разбивается на две подзадачи: быстрое построение графа вложенности и нахождение максимального независимого множества в этом графе. Заметим сразу, что если строка s2 является подстрокой строки s1, а строка s3 является подстрокой строки s2, то s3 очевидно является подстрокой строки s1. Таким образом, граф вложений зададаёт частично упорядоченное множество.
Для быстрого построения графа воспользуемся алгоритмом Ахо-Корасик. С помощью данной структуры мы построим все существенные рёбра графа, то есть такие рёбра  , что не найдётся w, такого что
, что не найдётся w, такого что  и
и  . Одним из возможных способов является:
. Одним из возможных способов является:
- Построить структуру Ахо-Корасик;
- Для каждой вершины найти и запомнить ближайшую терминальную в суффиксном пути;
- Ещё раз скормить каждую строку автомату Ахо-Корасик, при этом каждый раз после добавления очередного символа требуется проводить ребро в ближайшую терминальную вершину в суффиксном пути;
- Кроме существенных рёбер, данный алгоритм возможно добавит ещё какие-то корректные рёбра, но это никак не влияет на результат работы следующего шага;
- Транзитивно замкнуть построенный граф.
Для решение второй части данной задачи требует применить теорему Дилворта. Восстановление ответа следует из конструктивного доказательства теоремы.
Получаем O(L + n3) на построение графа + O(n3) на нахождение максимальной антицепи, итоговая сложность решения: O(L + n3), где L — суммарная длина всех строк.
Поздравляем ikatanic — единственного человека сдавшего эту задачу во время тура. Для дальнейшего уточнения решения предлагается посмотреть 13851141.
Упражнение: научитесь решать задачу с сохранением асимптотики, при условии что требуется найти множество строк максимальное не по размеру, а по суммарной длине.










Автокомментарий: текст был обновлен пользователем GlebsHP (предыдущая версия, новая версия, сравнить).
В задаче E можно делать первую часть за O(L+n^2). Для этого не нужно делать транзитивное замыкание, а пускать дфс по сжатым суффиксным ссылкам.
Почему это будет O(n2), ведь тебе нужно запустить дфс из каждой вершины, а рёбер порядка O(n2)?
UPD: sorry something was wrong on my side.
Автокомментарий: текст был обновлен пользователем GlebsHP (предыдущая версия, новая версия, сравнить).
You're going to take us places, GlebsHP. Great round!
Has anyone been able to come up with an O(1) solution for Div 1 — B?
Accepted solution: http://codeforces.net/contest/590/submission/13860359
Explanations: http://codeforces.net/blog/entry/21185?#comment-258444
Thanks!
check this out...(http://codeforces.net/contest/591/submission/13839965)
self explanatory O(n) :-)
Here's another solution in O(1) for Div1 — B:
Without loss of generality suppose x1 = y1 = 0. Clearly when the wind is the same, it is optimal to keep the velocity the same.
First, we check if we can get from start to finish in time <= T.
If we could, then there is a constant k (where the units of k is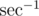 ) such that (here I am using vector notation so (a, b) denotes vector) |k(x2, y2) - (vx, vy)| = vmax.
) such that (here I am using vector notation so (a, b) denotes vector) |k(x2, y2) - (vx, vy)| = vmax.
We can simply square this equation, and this results in a quadratic in k, which we can solve.
If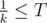 then we are done and we can simply take that value of
then we are done and we can simply take that value of 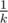 as our answer.
as our answer.
Otherwise, our solution is as follows:
Going from our starting point, the locus of points we can reach within time T is a circle which contains all the points of the form t(vmaxcos θ + vx, vmaxsin θ + vy). This is a circle with center ( - tvx, - tvy) and radius tvmax.
Say that we take g extra time to reach the end, where g is in seconds.
Going from our ending point, the locus of points we could have started at time T is a circle which contains all the points of the form (x2 + gvmaxcos θ - gwx, y2 + gvmaxcos θ - gyx). This is a circle with center (x2 - gwx, y2 - gyx) and radius gvmax.
Now our job is simply to check whether these two circles intersect; that is, if (distance_between_centers <= sum_of_radii). This results in a quadratic equation in g which we can also solve.
My code: 13927040
EDIT: Included submission. Also changed < to <=)
How do you solve those equations without known values for theta? Did you write four equations (two circles, two coordinates), then solve that as a system of four equations with three variables (theta1, theta2 and g)? I'm probably overcomplicating but I don't see how else I can fill in the blanks :D
θ is a parameter that I use to describe the geometric shape that I am talking about; it is not actually a variable I am solving for. For example, I could describe the unit circle as points of the form (cos θ, sinθ). Nice catch!
g is a variable that I am solving for.
In the quadratic equations that I mention in my explanation, I only have one unknown value (k and g).
что такое бамбук?
Граф являющийся цепочкой. Ещё называется линейный граф.
Actually, why do Div 1 and Div 2 always share 3 problems? Why not share 1 or 2 problems only? I think this can make the Div 1 and Div 2 rounds easier for Div 2 participants.
How to calculate upper limit for time in Div1 B?
Wait, so in the problem, Median Smoothing, there is not a single situation where the sequence will never become stable?
The tutorial for problem E gives a link to Dilworth theorem in Wikipedia. A few minutes ago I have read the inductive proof in Wikipedia and realized that it is wrong, and I've marked it in that article in Wikipedia. So, as the link is wrong, could you please give us an aditional hint on how to solve this independent set problem. Thanks.
My previous comment is wrong.
Can someone explain me the Div.1 A problem... I have been trying it for long now and after making observations,cant solve the problem as a whole,cant put those observations together.. Also,in the author's solution,they say that it's impossible for a series to be never stable..How can we proof that?!
Observations: 1) If value at i is equal to either value at i-1 or i+1,value at i will never change 2)Let p[i] denote the number of steps taken to make value at i stable.And we will use the above observation to mark all such pts 0,i.e p[i]=0.And p[1]=0 and p[n]=0.Let's call i with p[i]=0 as hinge,as it never changes. 3)At every step, hinges influence its surrounding pts and tries to make their value equal to it's. 4)So,calculate the nearest hinge for every point,i will be equal to the value of nearest hinge.
Lol, you explain better than the editorialist.
lol,after solving the problem,I read the editorial and I myself couldn't understand.
deleted nvm
How to solve the challenge of Div1E i.e. how to find the maximum weight antichain of a POSET? I tried googling but couldn't find a reasonable solution for this specific challenge.