Эта задача является чисто технической. Нужно было сделать ровно то, что написано в условии.
600B - Запросы о количестве не превосходящих элементов
Давайте отсортируем числа первого массива. Теперь будем идти по второму массиву и для текущего числа bj найдем бинарным поиском индекс первого большего числа в первом массива. Этот индекс и будет являться ответом.
Другим подходом в этой задаче было следующее: отсортируем оба массива сохранив при этом индексы чисел (например можно сортировать пары <значение, позиция>). Теперь будем идти по второму массиву и хранить переменную p — указатель на первый элемент ap такой, что он больше текущего bj. Поскольку оба массива отсортированы указатель можно не сбрасывать на каждой итерации, а просто двигать его дальше вправо.
Асимптотическая сложность решения: O(nlogn).
Давайте посчитаем для каждого символа c сколько раз он встречается в s. Обозначим эту величину cntc. Рассмотрим нечетные cntc. В палиндроме нечетных cntc может быть не больше одного. Пусть a1, a2...ak — это символы с нечетным cntc в алфавитном порядке. Заменим любой символ ak символом a1, символ ak - 1 символом a2 и так далее пока не дойдем середины. Теперь у нас имеется имеется не более одного нечетного символа. Если нечетный символ есть поставим его в середину ответа. А в первую половину возьмем от всех букв cntc / 2 в алфавитном порядке. Например, если s = aabcd мы сначала заменим d на b, после этого поставим символ c в середину и после перестановки остальных символов получим строку abcba.
Асимптотическая сложность решения: O(n).
600D - Площадь пересечения двух кругов
Давайте сразу отбросим случай когда круги не пересекаются, в это случае ответ равен 0. Это можно проверить в целых числах, сравнив квадрат расстояния между центра с квадратом суммы радиусов. Также отбросим случай, когда один круг полностью лежит внутри другого, в этом случае ответ есть площадь маленького круга. Это тоже можно проверить в целых числах, сравнив квадрат расстояния между центра с квадратом разности радиусов. Отлично теперь можно рассмотреть общий случай. Ответ будет складываться из некоторого сегмента первого круга и некоторого сегмента второго круга. Для того, чтобы определить угол первого сегмента рассмотрим треугольник, образованный центрами кругов и одной из точек пересечения. В этом треугольнике мы знаем все три стороны, значит по теореме косинусов может определить угол сегмента. Значит мы можем определить площадь сектора. Теперь остается вычесть из этого площадь треугольника образованного одним из центров и точками пересечения кругов. А это можно сделать, посчитав площадь как половина модуля псевдовекторного произведения. Таким образом получаются следующие формулы: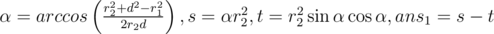 
,
где d — расстояние между центрами. И соответственно тоже самое нужно сделать для первого круга, поменяв индексы 1 ≤ ftrightarrow2.
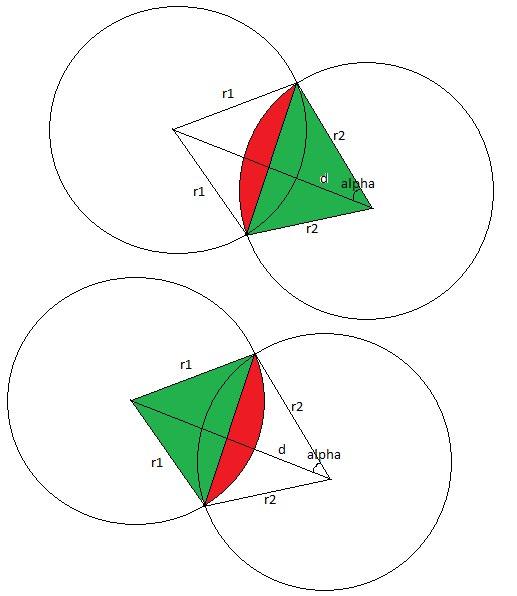
Асимптотическая сложность решения: O(1).
Название этой задачи является анаграммой к Small to large. И это не спроста :-) Авторское решение по этой задаче использует классическую технику пересчета множеств на дереве. Простейшим решением этой задачи является следующее: давайте для каждой вершины поддерживать один map<int, int> — для каждого цвета, сколько раз он встречается, один set<pair<int, int>> — пары количество повторений и цвет, и число sum являющееся суммой самых частых символов. Для того, чтобы посчитать эти величины для вершины v нужно сначала посчитать их для всех сыновей, а потом просто сливать эти значения. Такой подход правильный, но медленный (сложность получится O(n2logn)). Но давайте немного улучшим это решение, каждый раз когда нам надо склеить 2 map-а a и b, будем клеить меньший из них (просто итерируясь по нему) к большему (это и есть small to large). Давайте теперь рассмотрим цвет какой-нибудь вершины: каждый раз, когда он будет перекидываться из одного map-а в другой размер другого будет как минимум вдвое больше. Таким образом, это цвет поперебрасывается не более logn раз. Каждой перебрасывание делается за O(logn). Просуммировав это по всем вершинам получаем сложность O(nlog2n).
Также стоит заметить, что у некоторых участников было другое решение, но эта техника является общей и применяется в широком круге задач.
600F - Раскраска ребер двудольного графа
Введем обозначение d — наибольшая из степеней вершин в графе. Утверждение: ответ равен d. Докажем это утверждение, построив конструктивный алгоритм (он и будет решением задачи). Давайте красить ребра по очереди в любом порядке. Пусть текущее ребро (x, y). Если сейчас существует цвет c, который свободен и в вершине x и в вершине y, мы просто красим ребро в цвет c. Если такого цвета нет обязательно существует пара цветов c1, c2 такая, что c1 есть в x но нет в y, а цвет c2 есть в y но нет в x. Давайте освободим вершину y от цвета c2. Рассмотрим другой конец ребра исходящего из вершины y цвета c2. Пусть это вершина z. Если у вершины z цвет c1 свободен мы можем покрасить ребра x, y в цвет c2, а ребро y, z перекрасить в цвет c1. Таким образом мы проведем чередование. Если же у вершины z цвет c1 занят посмотрим на следующую вершину по цвету — w. Если это вершина не содержит ребра цвета c2 мы снова можем провести чередование. И так далее. Поскольку граф двудольный мы обязательно сможем найти чередующуюся цепочку. Поиск цепочки можно сделать обходом в глубину. Длина цепочки порядка O(n). Поэтому окончательно имеем:
Сложность решения: O(nm).
Автокомментарий: текст был обновлен пользователем Edvard (предыдущая версия, новая версия, сравнить).
Автокомментарий: текст был обновлен пользователем Edvard (предыдущая версия, новая версия, сравнить).
Немного не понял переход: " Давайте теперь рассмотрим цвет какой-нибудь вершины: каждый раз, когда он будет перекидываться из одного map-а в другой размер другого будет как минимум вдвое больше." Почему в худшем случае (цепь, в которой все вершины разного цвета) не получится очень большого размера массива мапов (порядка n^2)?
Вы случайно сказуемое? Памяти от нас потребуется явно не больше, чем времени. Что до времени — раз у нас каждый раз при перекидывании элемента размер его текущего множества увеличился хотя бы в два раза, у нас после k-го перебрасывания массив увеличился (по сравнению с размером до перемещений) хотя бы в 2k раз.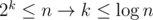
. Каждый элемент перебрасывался не больше 
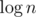раз. Значит, суммарно 
перебрасываний.
Разбор задачи F будет добавлен в скором времени?
http://homepages.cwi.nl/~lex/files/edgecol.pdf
Готово.
Какое?
Hi,
Do you have an English translated version of your blog?
Thanks.
I've done the first four problems. Working on the last two.
Fine. I am waiting for it. Eager to know the logic. Thanks. :)
Thank Edvard so much for this editorial!!
Автокомментарий: текст был обновлен пользователем Edvard (предыдущая версия, новая версия, сравнить).
Автокомментарий: текст был обновлен пользователем Edvard (предыдущая версия, новая версия, сравнить).
How do you ensure that your formulas are precise enough? It is pretty easy to come up with those formulas, however it is much harder to convince yourself (and guys preparing tests) that it will be sufficiently precise on tests like:
As one particular example, the formula found here (equation 13) is not precise enough, at least without BigDecimals, while the editorial's formula works with long double (and some double mixed in).
The only difference between my two submissions 14517685 — WA28 and 14533916 — AC is that the second uses the formula from the editorial, while the first is from the above link.
The two formulas are almost the same, but differ in one part that is subtracted. I think the reason is that the imprecise formula involves taking the square root of a product of four terms, which might compound the error or something. Could someone shed some light on this?
The way to ensure this is to avoid at all costs substration or addition of floating point numbers. If we are adding floating point numbers we'd better ensure they are of the same sign. In other words, stick with ints as long as you can. I saw two problems (not sure if they equally serious):
1) the acos(x) function is flat for x near to 1. So in these cases it would be preferable to determine the angle though asin. It is possible to calculate a precise length of the perpendicular from the circle crossing onto the line connecting the centers. I did it using Heron's formula for area of a triangle. Therefore we can use asin instead of acos.
2) calculating asin(x)-x for small x. I did it using Taylor series around x=0.
Solution: http://pastebin.com/LV5qaK1Q
i calculate sin alpha using the area of the triangle s = 1/2 * (r1 * dis)* sin(alpha) then i calculate s using s = sqrt(p * (p — r1) * (p — r2) * (p — dis)) then i get wrong answer on test 9 !! where dis is the distance between the centers of the circles why this happen?
Auto comment: topic has been updated by Edvard (previous revision, new revision, compare).
UPD. А, я понял, где у нас расходятся решения. Да, действительно O(nm).
Ну там же поиск в глубину однозначный поэтому он работает за O(n).
Could someone, please, provide a readable piece of code for problem E?
Thanks a lot.
E is such a nice task. It can be solved in n sqrt n (with MO alg), n log^2, n log n with centroids,n log n and even n * DSU :P
I'd like to learn all of these methods. Could you provide some good links for learning?
Thanks!
How do you solve it in nlogn and n*DSU?
N log N with no stl cheats is as follows: We'll use smaller to larger technique, but provide merging with no additional log. We'll maintain a vector for each component (it's like find & union) and support O(1) merging for each element in it. (therefore overall merge for 2 components will bo O(smaller)). Well known fact, subtree query could be changed into some preorder array contiguous segment query. This is not important at all, but we can come up with the idea of faster merging — a vertex of a colour X will always be merged first with the nearest vertex of colour X in preorder array. (Left or right, two cases). So we could preprocess for each colour all occurences of it and merge in O(1). Some additional arrays might be needed, but it's the main idea.
Do you happen to have code for this?
On task E, if our tree is a line of 10^5 nodes and value is different for each node. For every node we store all different colors in subtree of v in map, and in this case we should use N^2 memory, shouldnt we?
No, parent uses map of biggest son.
Is the memory complexity O(n*log(n)) ?
Did you get the answer?
Can anyone please explain the statement Let's replace any one of symbols ak with symbol a1, ak - 1 with a2 and so on until the middle of a. Now we have no more than one odd symbol. with sample string bbbcccddd
Why does my solution for 600A get TLE? http://codeforces.net/submissions/r4huln/
your solution is O(n square) and the input is too big for n square
So how should I solve this more efficiently?
use binary search as written in editorial
Can any one tell me what's the difference between __mingw_printf("%Lf") and cout when printing long double?
Here's my solution:
14537257 __mingw_printf
14536996 cout
which first one got Wrong Answer, and the second one got Accepted.
I'm totally confused.
Thanks a lot.
Hello, I have a question about Problem D. I fail to hack the solution with the Data like this:
The result should be pi*r^2 = pi*1e18 = 3141592653589793238.46264338. The answer should be at least in this interval:
on condition that the absolute error of area doesn't exceed 1e-6. ("The answer will be considered correct if the absolute or relative error doesn't exceed 10 - 6")
That is to say, we should not store pi in 80 or 96 bits long-double variable because we need at least first 24 digits of pi to get correct result for this data. I have checked the output of the code based on long double and confirmed that the absolute error of that solution > 1e-6, but I still got "Unsuccessful hacking attempt". Would you like to tell me the reason?
On the other hand, acosl(-1) = 3.141592653589793238512... here. Only first 19 digits of pi are correct and the absolute error will be about 1 (pi*1e18).
Thanks.
Solution can return result with relative error of 1e-6 rather than absolute error of 1e-6.
Thanks.
Правильно ли я понимаю, что D нерешаема без long double?
И что в MSVS ее не сдать без длинки (там long double <=> double)?
На этот тест
-999999999 0 1000000000
999999999 0 1000000000
В MSVS выдается ответ с погрешностью 20%. Если тот же код отправить в G++ => Accepted.
интересует тот же вопрос!
will you add codes for problems?
in problem F ..can we extend this solution to general graphs ?
If I am not wrong there is an algorithm to paint in d + 1 colours.
can you provide a link please ?
Sorry, I was thinking about vertex coloring, whereas in this problem you must color edges.
yes i think that should work ! thanks a lot ..but do you have a link for such problem on any online judge ?
Can someone explain Make Palindrome using editorial for the case bbbcccddd
cnt[b] = 3 , cnt[c] = 3 , cnt[d] = 3
all of them are odd so a1=b , a2=c , a3=d
replace one of a3 characters with a1 so cnt[b] = 4 , cnt[d] = 2
cnt[c] will remain odd but it is no matter. we can use one c at middle of palindrome.
so palindrome will be : bbcdcdcbb
My code is giving correct output for all the small test cases yet giving wrong answer on test 7 id: http://codeforces.net/contest/600/submission/14548282 can someone tell me where i am missing. I have tried to implement STL.
Please someone provide me cases .
your code gives wrong answer on these cases:
bluespeckisa
nass
holewhof
indsitmorere
spectfulto
livelikead
ogof
somefunnyredcoders
likexell
osbutt
hesadtruth
isxellos
dontfeelen
oughfu
ntogiveashit
toth
ismotherfucker
bitchandgets
angrywhenthisblues
hitmakesjokesf
orhisdearm
asterxelloss
if you want the correct answers for them see here: http://pastebin.com/ZmaE4npq
Thanks man there was bug in the case where i was handling the even length case. I had always looked at odd cases thinking even case to be perfectly fine but it just came the opposite.
Can anyone explain more clearly why the "Small to large" trick reduce the solution complexity to O(n log n) in problem E? Thanks in advance.
Hello there! I'm having the same question as you. Have you managed to figured it out ? Can you please elaborate ?
Maybe this comment will help.
Where to find theory or some examples related to the small to large technique used in Problem E — Lomsat gelral ?
Read the proof of Union by Rank algorithm: [here](http://www.wikiwand.com/en/Proof_of_O(log*n)_time_complexity_of_union%E2%80%93find)
I'm using binary search (http://ideone.com/P63MMj ) in 600B but still get TLE. Any ideas why?
The problem is in Arrays.sort. It uses quicksort and there are anti-quicksort tests in this problem now.
For Problem E, can anyone explain "Let's consider some vertex v: every time when vertex v will be moved from one map to another the size of the new map will be at least two times larger." ?
In problem E, I understood the technique of Small to Large. But I have one doubt, if all nodes have different colors, won't all the maps take O(n^2) memory?
I guess I just thought of its logn complexity as a black-box. Now on further thinking, I guess when 2 sets of size s1 and s2 are merged to get a new set of size s3, total memory spaced needed along with the space needed for new set is s3 + min(s1, s2). Moreover, s3 < = (s1 + s2).
I didnt get the same thing...
why solutions are not visible of this round?
https://codeforces.net/contest/600/submission/59420840 Plz explain what's wrong?
You have a 2D array which size is N*N, but MAXN = 1e5 => N*N=1e10, but it's too much
Could anyone show me a detailed proof or explaination for the reduction of time complexity in problem E.Lomsat gelral when using smaller to larger technique?
Really appreciate for your help <3. I have been contemplating this for nearly a week and still haven't figured stuff out :<.
You need to consider Heavy Light Decomposition of the tree. Number of ancestors of u that traverse u is equal to number of light edges on path from u to the root which is O(log n). Thus, each node is traversed O(log n) times.
In problem 4, I am getting wrong ans at test case no. 34 and my ans is off by (.02). But I guess that my way evaluating area kite which is (p*q)/2 where (p is diagonal 1 and q is diagonal 2) is more accurate as it involves less rounded off values. Can it happen that my solution is more accurate than a given solution or please correct me if I am doing anything wrong? Below is the link to my submission:- https://codeforces.net/contest/600/submission/79322952
I am also facing the same issue.
why is the memory complexity not O(n^2)?
Like for example if we have n nodes connected in a straight line and each node has color = index,
then on merging ,each time the parent's map will have one more element than the child's map and sum of elements would be like sum = 1 + 2 + 3 .... + n — 1 + n.
can anyone please tell where i am wrong?
Is it possible to solve problem '600E-Lomsat gelral' with mo's algorithm? My solution id is 189869200
No