Вот две задачи по терверу, которые сами по себе довольно простые и не неожиданные, но в них на мой вкус очень забавные ответы. Итак...
1. Представьте себе, что мы хотим сгенерировать случайный бит следующим странным способом. Возьмем очень-очень большое натуральное n и случайный двудольный граф, в каждой доле которого по n вершин. Посчитаем в нем количество совершенных паросочетаний (наборов из n ребер, которые не имеют общих концов). Четность этого количества и будет нашим битом. Какова вероятность, что этот бит будет равен нулю?
2. Представьте себе, что у нас есть n корзинок, в которые мы случайно бросаем шары. Мы продолжаем процесс, пока в каждой корзинке не будет по крайней мере m шаров. Сколько в среднем шаров мы бросим? Интересует ответ с точностью до константы. Например, хорошо известно, что если m = 1, то в среднем мы бросим 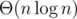 шаров.
шаров.
→ Pay attention
Before contest
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
23:20:26
Register now »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
23:20:26
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Find user
→ Recent actions
Write comment?
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/22/2024 18:14:35 (i2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










