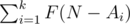Блог пользователя agul

Количество разбиений в суммы слагаемых
Автор agul, 13 лет назад, По-русски

Не знаю, как точно сформулировать вопрос, поэтому постараюсь писать подробно.


Пусть мне дано некоторое множество чисел [A1, A2, A3,  ... , Ak] - множество возможных слагаемых и дано число N, которое нужно разложить в суммы слагаемых (слагаемые являются числами множества).

Например:
N=8
A=[1, 2, 6]

Возможные разбиения:

8=6+2
8=6+1+1
8=2+2+2+2
8=1+1+2+2+2
8=1+1+1+1+2+2
8=1+1+1+1+1+1+2
8=1+1+1+1+1+1+1+1

Ответ в данном случае - 7.

Существует ли какой-то алгоритм подсчета ответа по заданному числу N (предполагается, что множество A дано в условии и постоянно на всех тестах).

Можете написать алгоритм прямо в комментариях, или дать ссылки на хорошие статьи, или просто отправить в Google по хорошему запросу, где много можно почитать.

Заранее спасибо!
  • Проголосовать: нравится
  • -2
  • Проголосовать: не нравится

13 лет назад, # |
← Rev. 2   Проголосовать: нравится +1 Проголосовать: не нравится

Можно динамикой за O(NK).

Пусть f(i,j) это количество разбиений на слагаемые числа i, если использовать только первые j слагаемых из набора. Тогда можно записать следующее рекуррентное соотношение:
f(0,j) = 1
f(i,j) = f(i-a_j,j)+f(i,j-1).
→ Ответить
  • 13 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится
    http://pastebin.com/ZqymDhdQ

    Почему-то все равно работает неверно.
    Можете подсказать, где ошибка?
    → Ответить
    • 13 лет назад, # ^ |
        Проголосовать: нравится +1 Проголосовать: не нравится
      f[0][0] = 1
      → Ответить
    • 13 лет назад, # ^ |
        Проголосовать: нравится +1 Проголосовать: не нравится
      А, это я перепутал. Там не f(i,0) = 1, а f(0,j) = 1.
      → Ответить
      • 13 лет назад, # ^ |
          Проголосовать: нравится 0 Проголосовать: не нравится
        Возник вопрос по данной динамики.
        Предположим у нас есть набор A = [1, 2], k = 2.
        N = 1 : 
        dp[1][2] = 1.
        Ответ : 1 
        N = 2 : 
        dp[1][1] = 1;
        dp[1][2] = 2;   
        Ответ : 2
        N = 3 :
        перебираем кол-во первых слагаемых из набора
        j = 1 : 
        dp[3][1] = 1    (1 + 1 + 1);
        j = 2 : По нашей реккуретной формуле мы должны взять
        dp[3 - a[2][2] + a[3][1] = dp[1][2] + dp[3][1]
        dp[1][2] = 0, и это понятно - мы не можем набрать цифру 1 
        из двух слагаемых из набора.
        dp[3][1] = 1, возможен только случай 1 + 1 + 1
        Следовательно получается dp[3][2] = 1;
        Тогда получается что при N = 3, dp[3][1] = 1 , то есть только одним способов, хотя способов на самом деле = 2 (1 + 1 + 1, 1 + 2).


        → Ответить
13 лет назад, # |
← Rev. 2   Проголосовать: нравится +1 Проголосовать: не нравится

А просто написать такую динамику: d[i][j], где i-уже набранная сумма, j-последнее число. Храним в этой динамике количество различных сумм, переход делаем если j>=next
→ Ответить
13 лет назад, # |
← Rev. 3   Проголосовать: нравится +3 Проголосовать: не нравится

Такая задача решается динамическим программированием.
Введем функцию F(N) - число способов разбить число N на слагаемые из множества A1 ... Ak. Предположим, что F(0) = 1. В остальных случаях можно выразить F(N) с помощью рекурентной формулы:
Очевидно, что суммировать необходимо только для неотрицательных величин N - Ai.
Алгоритм можно реализовать с асимптотикой O(NK). В самой простой реализации можно просто перебирать итератор i от 1 до N и вычислять F(i) суммированием необходимых слагаемых.
 
P.S. Вышеописанное решение работает в случае, если порядок слагаемых в разбиении важен. В данном случае, это не так. Поэтому лучше воспользоваться решением, описанным выше:
F(N, t) = F(N - At, t) + F(N, t + 1)
Здесь конечными состояниями являются F(0, x) = 1, F(N, K + 1) = 0.
Более подробно идея этого решения описана выше.
→ Ответить
13 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится
Спасибо большое всем отписавшимся, если вдруг кому-нибудь когда-нибудь понадобится, то вот мой итоговый код: http://pastebin.com/cyQh6REj
→ Ответить