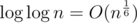Блог пользователя rahul_1234

Time Complexity
Автор rahul_1234, история, 9 лет назад, По-английски

Can anybodyt help to find complexity oof this algo: T(n) = n^ (1/3) T( sqrt( n) ) + 2n

I solved it and found it be O(n) but is it correct? Please confirm.

  • Проголосовать: нравится
  • +20
  • Проголосовать: не нравится

»
9 лет назад, # |
  Проголосовать: нравится +5 Проголосовать: не нравится

You can keep expanding T(n). By doing this, you get:

The first term is equal to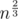 as n gets large, since the sum in the exponent is a geometric series.

There are only log(log(n)) terms of the other kind. Proof: say that i is the last number for which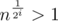 . Then 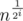is approximately 2 (or 3, but if it is bigger we can take the root of that to get i+1), so we can take the logarithm from both sides of the equation 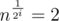. This results in 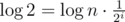, so 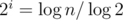. Then we find for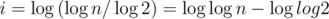

Every term of that kind have an exponent between 2/3 and 1. Say that we start counting these terms from i=0. Then the i'th term has an exponent equal to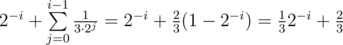 . So as you can see for i=0, this exponent is equal to 1, but as i gets larger, this exponent tends to 2/3.

As n gets larger and larger, there are many more terms with exponents 2/3 than 1. So as n becomes large, the majority of the terms have an exponent which is approximately 2/3. Therefore the complexity of this algorithm is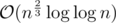

→ Ответить
  • »
    »
    9 лет назад, # ^ |
    ← Rev. 3   Проголосовать: нравится +10 Проголосовать: не нравится

    Shouldn't the upperbound be n as when exponent at i=0; exponent is 1. O( n + ( ( n^(2/3) ) * log( log(n) ) == O( n )?

    → Ответить
    • »
      »
      »
      9 лет назад, # ^ |
        Проголосовать: нравится -10 Проголосовать: не нравится

      Well, O(n) is a bit too small I guess. You could say that it is of order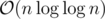 , because every term is smaller than 2n. I think the actual complexity of this algorithm is of the form 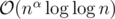where α is a number between and 1.

      This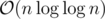 complexity differs from 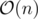with a maximum factor of 6 for n smaller than 264, so you wouldn't see any difference for 'small' values of n. Still as n gets larger, this factor keeps increasing.

      → Ответить
  • »
    »
    9 лет назад, # ^ |
      Проголосовать: нравится +3 Проголосовать: не нравится

    It's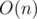 , because is 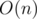and each other summand is 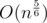and there is 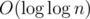summands: 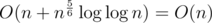, because

    → Ответить